PAC Reinforcement Learning with Rich Observations

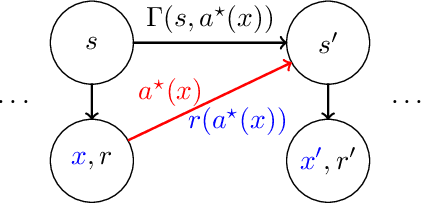
We propose and study a new model for reinforcement learning with rich observations, generalizing contextual bandits to sequential decision making. These models require an agent to take actions based on observations (features) with the goal of achieving long-term performance competitive with a large set of policies. To avoid barriers to sample-efficient learning associated with large observation spaces and general POMDPs, we focus on problems that can be summarized by a small number of hidden states and have long-term rewards that are predictable by a reactive function class. In this setting, we design and analyze a new reinforcement learning algorithm, Least Squares Value Elimination by Exploration. We prove that the algorithm learns near optimal behavior after a number of episodes that is polynomial in all relevant parameters, logarithmic in the number of policies, and independent of the size of the observation space. Our result provides theoretical justification for reinforcement learning with function approximation.

Exploratory Gradient Boosting for Reinforcement Learning in Complex Domains

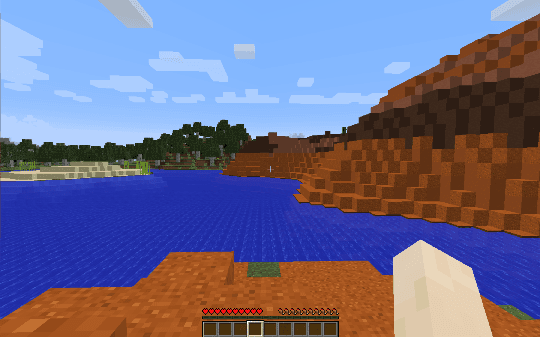
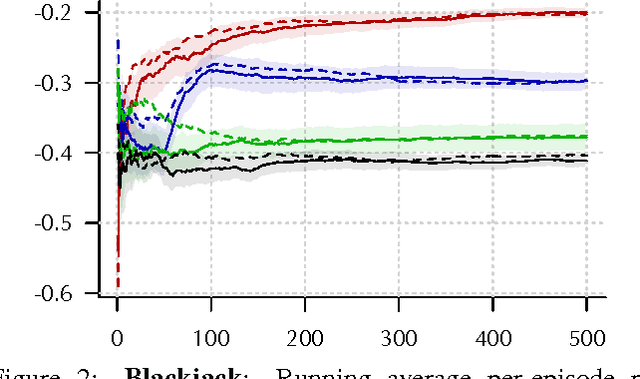
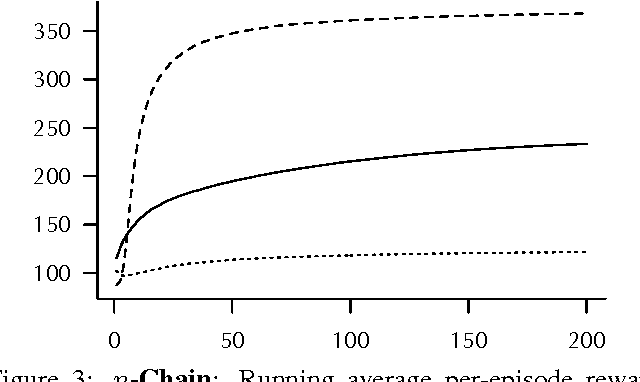
High-dimensional observations and complex real-world dynamics present major challenges in reinforcement learning for both function approximation and exploration. We address both of these challenges with two complementary techniques: First, we develop a gradient-boosting style, non-parametric function approximator for learning on $Q$-function residuals. And second, we propose an exploration strategy inspired by the principles of state abstraction and information acquisition under uncertainty. We demonstrate the empirical effectiveness of these techniques, first, as a preliminary check, on two standard tasks (Blackjack and $n$-Chain), and then on two much larger and more realistic tasks with high-dimensional observation spaces. Specifically, we introduce two benchmarks built within the game Minecraft where the observations are pixel arrays of the agent's visual field. A combination of our two algorithmic techniques performs competitively on the standard reinforcement-learning tasks while consistently and substantially outperforming baselines on the two tasks with high-dimensional observation spaces. The new function approximator, exploration strategy, and evaluation benchmarks are each of independent interest in the pursuit of reinforcement-learning methods that scale to real-world domains.

Efficient and Parsimonious Agnostic Active Learning

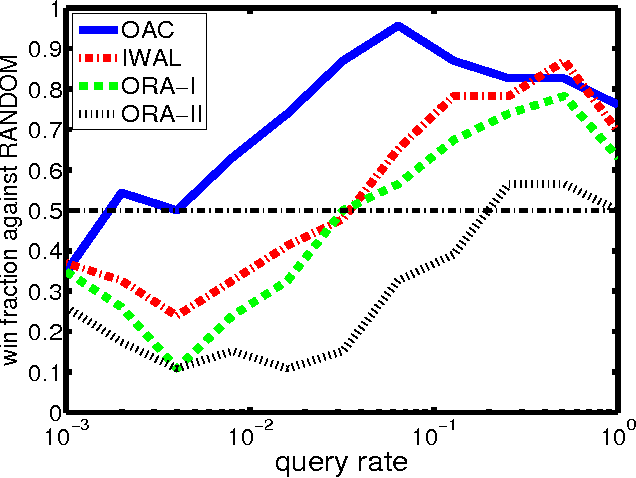
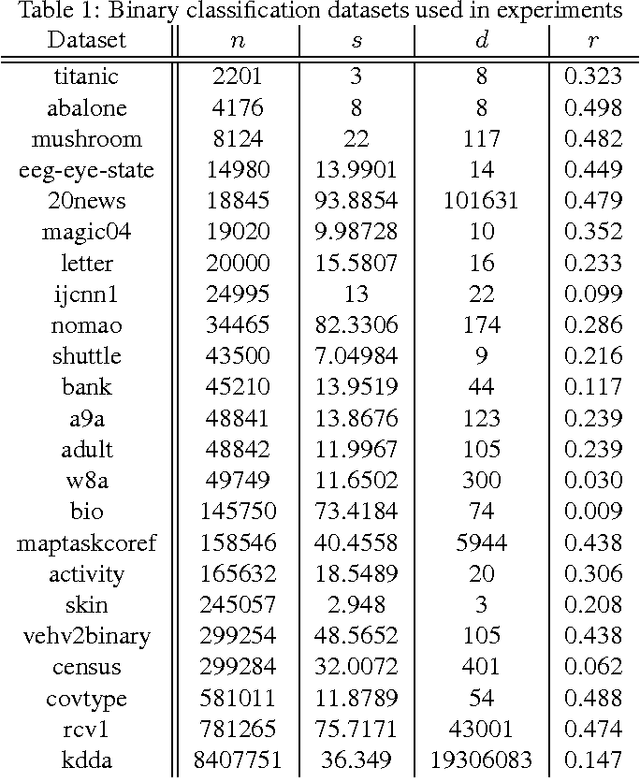
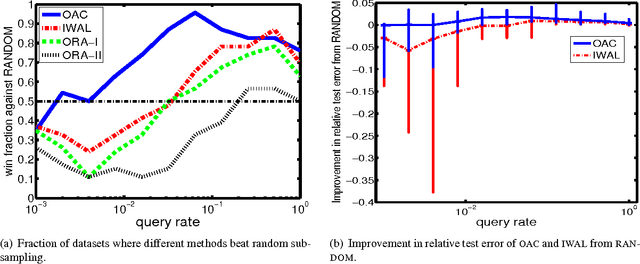
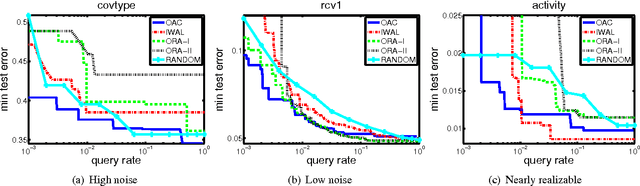
We develop a new active learning algorithm for the streaming setting satisfying three important properties: 1) It provably works for any classifier representation and classification problem including those with severe noise. 2) It is efficiently implementable with an ERM oracle. 3) It is more aggressive than all previous approaches satisfying 1 and 2. To do this we create an algorithm based on a newly defined optimization problem and analyze it. We also conduct the first experimental analysis of all efficient agnostic active learning algorithms, evaluating their strengths and weaknesses in different settings.

Fast Convergence of Regularized Learning in Games

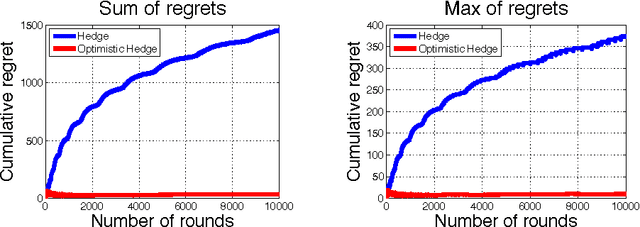
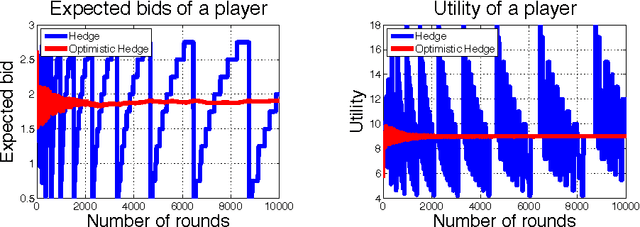
We show that natural classes of regularized learning algorithms with a form of recency bias achieve faster convergence rates to approximate efficiency and to coarse correlated equilibria in multiplayer normal form games. When each player in a game uses an algorithm from our class, their individual regret decays at $O(T^{-3/4})$, while the sum of utilities converges to an approximate optimum at $O(T^{-1})$--an improvement upon the worst case $O(T^{-1/2})$ rates. We show a black-box reduction for any algorithm in the class to achieve $\tilde{O}(T^{-1/2})$ rates against an adversary, while maintaining the faster rates against algorithms in the class. Our results extend those of [Rakhlin and Shridharan 2013] and [Daskalakis et al. 2014], who only analyzed two-player zero-sum games for specific algorithms.

A Lower Bound for the Optimization of Finite Sums

This paper presents a lower bound for optimizing a finite sum of $n$ functions, where each function is $L$-smooth and the sum is $\mu$-strongly convex. We show that no algorithm can reach an error $\epsilon$ in minimizing all functions from this class in fewer than $\Omega(n + \sqrt{n(\kappa-1)}\log(1/\epsilon))$ iterations, where $\kappa=L/\mu$ is a surrogate condition number. We then compare this lower bound to upper bounds for recently developed methods specializing to this setting. When the functions involved in this sum are not arbitrary, but based on i.i.d. random data, then we further contrast these complexity results with those for optimal first-order methods to directly optimize the sum. The conclusion we draw is that a lot of caution is necessary for an accurate comparison, and identify machine learning scenarios where the new methods help computationally.

Learning to Search Better Than Your Teacher

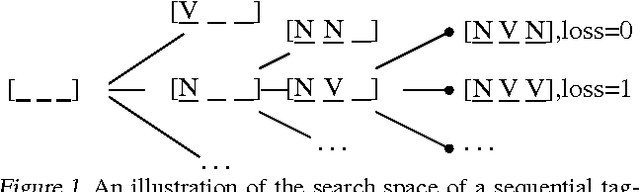
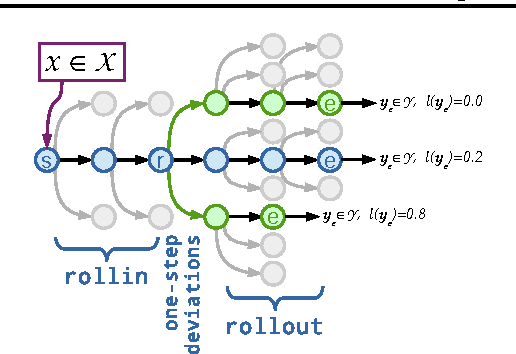
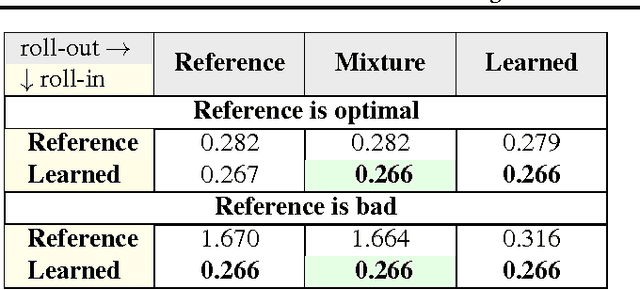
Methods for learning to search for structured prediction typically imitate a reference policy, with existing theoretical guarantees demonstrating low regret compared to that reference. This is unsatisfactory in many applications where the reference policy is suboptimal and the goal of learning is to improve upon it. Can learning to search work even when the reference is poor? We provide a new learning to search algorithm, LOLS, which does well relative to the reference policy, but additionally guarantees low regret compared to deviations from the learned policy: a local-optimality guarantee. Consequently, LOLS can improve upon the reference policy, unlike previous algorithms. This enables us to develop structured contextual bandits, a partial information structured prediction setting with many potential applications.

Taming the Monster: A Fast and Simple Algorithm for Contextual Bandits

We present a new algorithm for the contextual bandit learning problem, where the learner repeatedly takes one of $K$ actions in response to the observed context, and observes the reward only for that chosen action. Our method assumes access to an oracle for solving fully supervised cost-sensitive classification problems and achieves the statistically optimal regret guarantee with only $\tilde{O}(\sqrt{KT/\log N})$ oracle calls across all $T$ rounds, where $N$ is the number of policies in the policy class we compete against. By doing so, we obtain the most practical contextual bandit learning algorithm amongst approaches that work for general policy classes. We further conduct a proof-of-concept experiment which demonstrates the excellent computational and prediction performance of (an online variant of) our algorithm relative to several baselines.

Scalable Nonlinear Learning with Adaptive Polynomial Expansions

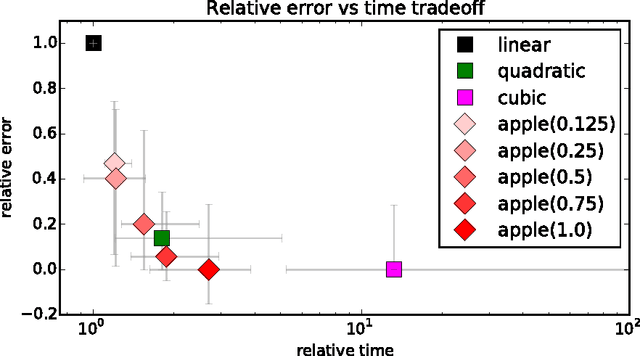
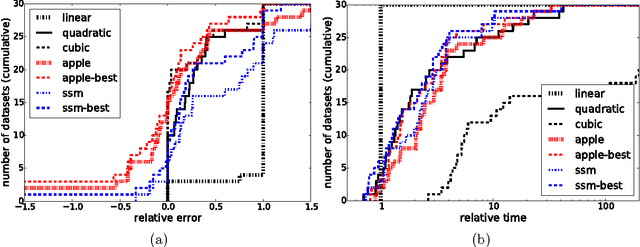
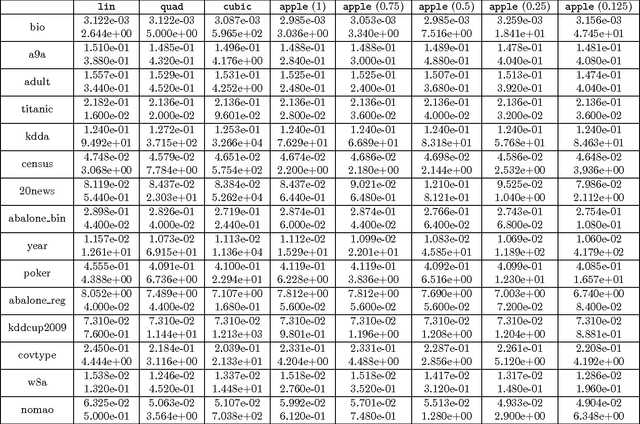
Can we effectively learn a nonlinear representation in time comparable to linear learning? We describe a new algorithm that explicitly and adaptively expands higher-order interaction features over base linear representations. The algorithm is designed for extreme computational efficiency, and an extensive experimental study shows that its computation/prediction tradeoff ability compares very favorably against strong baselines.

Learning Sparsely Used Overcomplete Dictionaries via Alternating Minimization

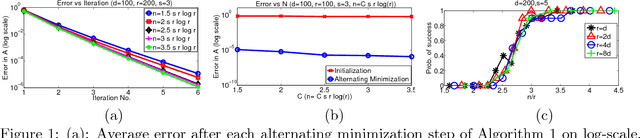
We consider the problem of sparse coding, where each sample consists of a sparse linear combination of a set of dictionary atoms, and the task is to learn both the dictionary elements and the mixing coefficients. Alternating minimization is a popular heuristic for sparse coding, where the dictionary and the coefficients are estimated in alternate steps, keeping the other fixed. Typically, the coefficients are estimated via $\ell_1$ minimization, keeping the dictionary fixed, and the dictionary is estimated through least squares, keeping the coefficients fixed. In this paper, we establish local linear convergence for this variant of alternating minimization and establish that the basin of attraction for the global optimum (corresponding to the true dictionary and the coefficients) is $\order{1/s^2}$, where $s$ is the sparsity level in each sample and the dictionary satisfies RIP. Combined with the recent results of approximate dictionary estimation, this yields provable guarantees for exact recovery of both the dictionary elements and the coefficients, when the dictionary elements are incoherent.

A Clustering Approach to Learn Sparsely-Used Overcomplete Dictionaries

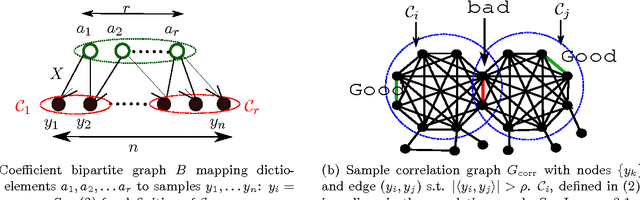
We consider the problem of learning overcomplete dictionaries in the context of sparse coding, where each sample selects a sparse subset of dictionary elements. Our main result is a strategy to approximately recover the unknown dictionary using an efficient algorithm. Our algorithm is a clustering-style procedure, where each cluster is used to estimate a dictionary element. The resulting solution can often be further cleaned up to obtain a high accuracy estimate, and we provide one simple scenario where $\ell_1$-regularized regression can be used for such a second stage.