PASS: Ambiguity Guided Subsets for Scalable Classical and Quantum Constrained Clustering

Pairwise-constrained clustering augments unsupervised partitioning with side information by enforcing must-link (ML) and cannot-link (CL) constraints between specific samples, yielding labelings that respect known affinities and separations. However, ML and CL constraints add an extra layer of complexity to the clustering problem, with current methods struggling in data scalability, especially in niche applications like quantum or quantum-hybrid clustering. We propose PASS, a pairwise-constraints and ambiguity-driven subset selection framework that preserves ML and CL constraints satisfaction while allowing scalable, high-quality clustering solution. PASS collapses ML constraints into pseudo-points and offers two selectors: a constraint-aware margin rule that collects near-boundary points and all detected CL violations, and an information-geometric rule that scores points via a Fisher-Rao distance derived from soft assignment posteriors, then selects the highest-information subset under a simple budget. Across diverse benchmarks, PASS attains competitive SSE at substantially lower cost than exact or penalty-based methods, and remains effective in regimes where prior approaches fail.

Beyond Variance: Knowledge-Aware LLM Compression via Fisher-Aligned Subspace Diagnostics

Post-training activation compression is essential for deploying Large Language Models (LLMs) on resource-constrained hardware. However, standard methods like Singular Value Decomposition (SVD) are gradient-blind: they preserve high-variance dimensions regardless of their impact on factual knowledge preservation. We introduce Fisher-Aligned Subspace Compression (FASC), a knowledge-aware compression framework that selects subspaces by directly modeling activation-gradient coupling, minimizing a second-order surrogate of the loss function. FASC leverages the Fisher Information Matrix to identify dimensions critical for factual knowledge, which often reside in low-variance but high-gradient-sensitivity subspaces. We propose the Dependence Violation Score (\r{ho}) as a general-purpose diagnostic metric that quantifies activation-gradient coupling, revealing where factual knowledge is stored within transformer architectures. Extensive experiments on Mistral-7B and Llama-3-8B demonstrate that FASC preserves 6-8% more accuracy on knowledge-intensive benchmarks (MMLU, LAMA) compared to variance-based methods at 50% rank reduction, effectively enabling a 7B model to match the factual recall of a 13B uncompressed model. Our analysis reveals that \r{ho} serves as a fundamental signal of stored knowledge, with high-\r{ho} layers emerging only when models internalize factual associations during training.

Beyond Perfect Scores: Proof-by-Contradiction for Trustworthy Machine Learning

Machine learning (ML) models show strong promise for new biomedical prediction tasks, but concerns about trustworthiness have hindered their clinical adoption. In particular, it is often unclear whether a model relies on true clinical cues or on spurious hierarchical correlations in the data. This paper introduces a simple yet broadly applicable trustworthiness test grounded in stochastic proof-by-contradiction. Instead of just showing high test performance, our approach trains and tests on spurious labels carefully permuted based on a potential outcomes framework. A truly trustworthy model should fail under such label permutation; comparable accuracy across real and permuted labels indicates overfitting, shortcut learning, or data leakage. Our approach quantifies this behavior through interpretable Fisher-style p-values, which are well understood by domain experts across medical and life sciences. We evaluate our approach on multiple new bacterial diagnostics to separate tasks and models learning genuine causal relationships from those driven by dataset artifacts or statistical coincidences. Our work establishes a foundation to build rigor and trust between ML and life-science research communities, moving ML models one step closer to clinical adoption.

Focus on What Matters: Fisher-Guided Adaptive Multimodal Fusion for Vulnerability Detection

Software vulnerability detection is a critical task for securing software systems and can be formulated as a binary classification problem: given a code snippet, determine whether it contains a vulnerability. Existing multimodal approaches typically fuse Natural Code Sequence (NCS) representations from pretrained language models with Code Property Graph (CPG) representations from graph neural networks, often under the implicit assumption that adding a modality necessarily yields extra information. In practice, sequence and graph representations can be redundant, and fluctuations in the quality of the graph modality can dilute the discriminative signal of the dominant modality. To address this, we propose TaCCS-DFA, a framework that introduces Fisher information as a geometric measure of how sensitive feature directions are to the classification decision, enabling task-oriented complementary fusion. TaCCS-DFA online estimates a low-rank principal Fisher subspace and restricts cross-modal attention to task-sensitive directions, thereby retrieving structural features from CPG that complement the sequence modality; meanwhile, an adaptive gating mechanism dynamically adjusts the contribution of the graph modality for each sample to suppress noise propagation. Our analysis shows that, under an isotropic perturbation assumption, the proposed mechanism admits a tighter risk bound than conventional full-spectrum attention. Experiments on BigVul, Devign, and ReVeal show that TaCCS-DFA achieves strong performance across multiple backbones. With CodeT5 as the backbone, TaCCS-DFA reaches an F1 score of 87.80\% on the highly imbalanced BigVul dataset, improving over a strong baseline Vul-LMGNNs by 6.3 percentage points while maintaining low calibration error and computational overhead.

HATS: High-Accuracy Triple-Set Watermarking for Large Language Models

Misuse of LLM-generated text can be curbed by watermarking techniques that embed implicit signals into the output. We propose a watermark that partitions the vocabulary at each decoding step into three sets (Green/Yellow/Red) with fixed ratios and restricts sampling to the Green and Yellow sets. At detection time, we replay the same partitions, compute Green-enrichment and Red-depletion statistics, convert them to one-sided z-scores, and aggregate their p-values via Fisher's method to decide whether a passage is watermarked. We implement generation, detection, and testing on Llama 2 7B, and evaluate true-positive rate, false-positive rate, and text quality. Results show that the triple-partition scheme achieves high detection accuracy at fixed FPR while preserving readability.

Weighted Stochastic Differential Equation to Implement Wasserstein-Fisher-Rao Gradient Flow

Score-based diffusion models currently constitute the state of the art in continuous generative modeling. These methods are typically formulated via overdamped or underdamped Ornstein--Uhlenbeck-type stochastic differential equations, in which sampling is driven by a combination of deterministic drift and Brownian diffusion, resulting in continuous particle trajectories in the ambient space. While such dynamics enjoy exponential convergence guarantees for strongly log-concave target distributions, it is well known that their mixing rates deteriorate exponentially in the presence of nonconvex or multimodal landscapes, such as double-well potentials. Since many practical generative modeling tasks involve highly non-log-concave target distributions, considerable recent effort has been devoted to developing sampling schemes that improve exploration beyond classical diffusion dynamics. A promising line of work leverages tools from information geometry to augment diffusion-based samplers with controlled mass reweighting mechanisms. This perspective leads naturally to Wasserstein--Fisher--Rao (WFR) geometries, which couple transport in the sample space with vertical (reaction) dynamics on the space of probability measures. In this work, we formulate such reweighting mechanisms through the introduction of explicit correction terms and show how they can be implemented via weighted stochastic differential equations using the Feynman--Kac representation. Our study provides a preliminary but rigorous investigation of WFR-based sampling dynamics, and aims to clarify their geometric and operator-theoretic structure as a foundation for future theoretical and algorithmic developments.

Bridging Training and Merging Through Momentum-Aware Optimization

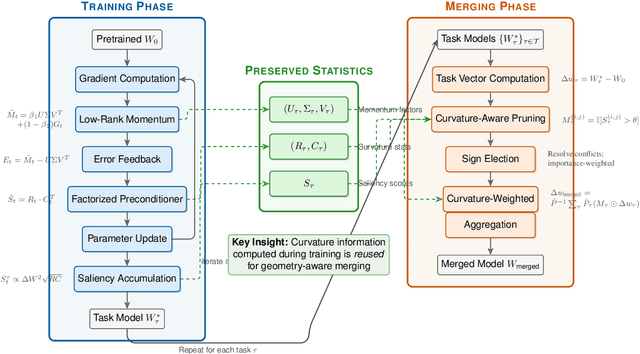
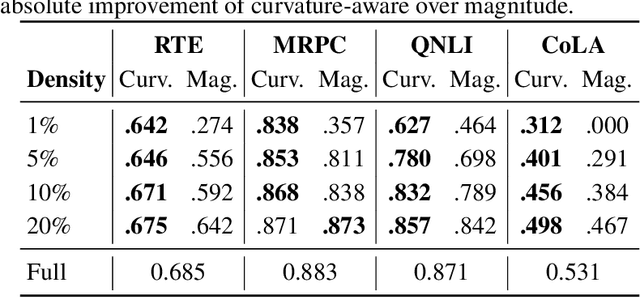
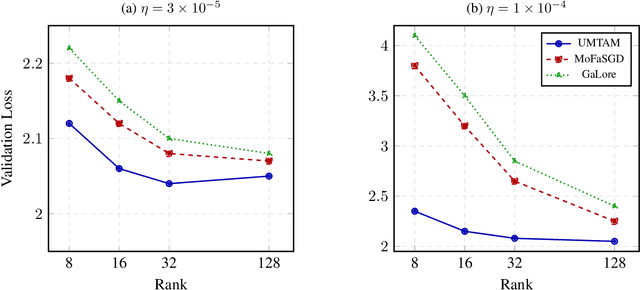
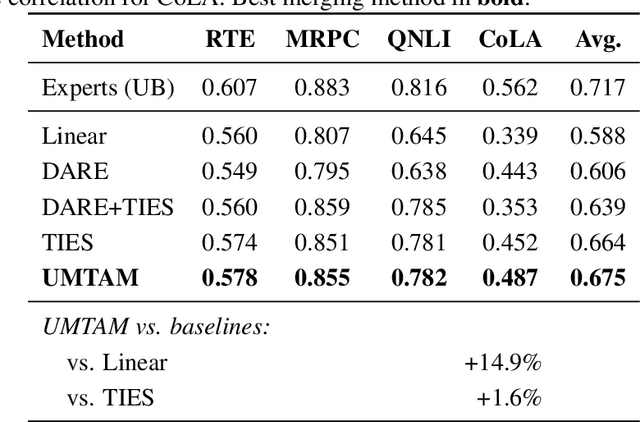
Training large neural networks and merging task-specific models both exploit low-rank structure and require parameter importance estimation, yet these challenges have been pursued in isolation. Current workflows compute curvature information during training, discard it, then recompute similar information for merging -- wasting computation and discarding valuable trajectory data. We introduce a unified framework that maintains factorized momentum and curvature statistics during training, then reuses this information for geometry-aware model composition. The proposed method achieves memory efficiency comparable to state-of-the-art approaches while accumulating task saliency scores that enable curvature-aware merging without post-hoc Fisher computation. We establish convergence guarantees for non-convex objectives with approximation error bounded by gradient singular value decay. On natural language understanding benchmarks, curvature-aware parameter selection outperforms magnitude-only baselines across all sparsity levels, with multi-task merging improving over strong baselines. The proposed framework exhibits rank-invariant convergence and superior hyperparameter robustness compared to existing low-rank optimizers. By treating the optimization trajectory as a reusable asset rather than discarding it, our approach eliminates redundant computation while enabling more principled model composition.

Simulation-Based Fitting of Intractable Models via Sequential Sampling and Local Smoothing

This paper presents a comprehensive algorithm for fitting generative models whose likelihood, moments, and other quantities typically used for inference are not analytically or numerically tractable. The proposed method aims to provide a general solution that requires only limited prior information on the model parameters. The algorithm combines a global search phase, aimed at identifying the region of the solution, with a local search phase that mimics a trust region version of the Fisher scoring algorithm for computing a quasi-likelihood estimator. Comparisons with alternative methods demonstrate the strong performance of the proposed approach. An R package implementing the algorithm is available on CRAN.

Soft Conflict-Resolution Decision Transformer for Offline Multi-Task Reinforcement Learning

Multi-task reinforcement learning (MTRL) seeks to learn a unified policy for diverse tasks, but often suffers from gradient conflicts across tasks. Existing masking-based methods attempt to mitigate such conflicts by assigning task-specific parameter masks. However, our empirical study shows that coarse-grained binary masks have the problem of over-suppressing key conflicting parameters, hindering knowledge sharing across tasks. Moreover, different tasks exhibit varying conflict levels, yet existing methods use a one-size-fits-all fixed sparsity strategy to keep training stability and performance, which proves inadequate. These limitations hinder the model's generalization and learning efficiency. To address these issues, we propose SoCo-DT, a Soft Conflict-resolution method based by parameter importance. By leveraging Fisher information, mask values are dynamically adjusted to retain important parameters while suppressing conflicting ones. In addition, we introduce a dynamic sparsity adjustment strategy based on the Interquartile Range (IQR), which constructs task-specific thresholding schemes using the distribution of conflict and harmony scores during training. To enable adaptive sparsity evolution throughout training, we further incorporate an asymmetric cosine annealing schedule to continuously update the threshold. Experimental results on the Meta-World benchmark show that SoCo-DT outperforms the state-of-the-art method by 7.6% on MT50 and by 10.5% on the suboptimal dataset, demonstrating its effectiveness in mitigating gradient conflicts and improving overall multi-task performance.

Fisher meets Feynman: score-based variational inference with a product of experts

We introduce a highly expressive yet distinctly tractable family for black-box variational inference (BBVI). Each member of this family is a weighted product of experts (PoE), and each weighted expert in the product is proportional to a multivariate $t$-distribution. These products of experts can model distributions with skew, heavy tails, and multiple modes, but to use them for BBVI, we must be able to sample from their densities. We show how to do this by reformulating these products of experts as latent variable models with auxiliary Dirichlet random variables. These Dirichlet variables emerge from a Feynman identity, originally developed for loop integrals in quantum field theory, that expresses the product of multiple fractions (or in our case, $t$-distributions) as an integral over the simplex. We leverage this simplicial latent space to draw weighted samples from these products of experts -- samples which BBVI then uses to find the PoE that best approximates a target density. Given a collection of experts, we derive an iterative procedure to optimize the exponents that determine their geometric weighting in the PoE. At each iteration, this procedure minimizes a regularized Fisher divergence to match the scores of the variational and target densities at a batch of samples drawn from the current approximation. This minimization reduces to a convex quadratic program, and we prove under general conditions that these updates converge exponentially fast to a near-optimal weighting of experts. We conclude by evaluating this approach on a variety of synthetic and real-world target distributions.