Bridging Training and Merging Through Momentum-Aware Optimization

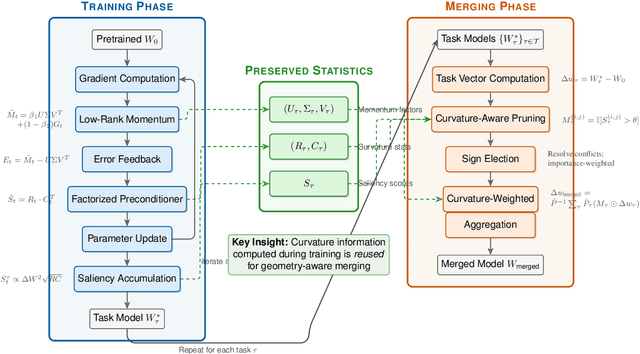
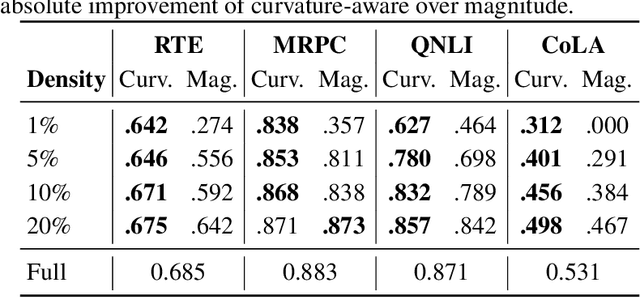
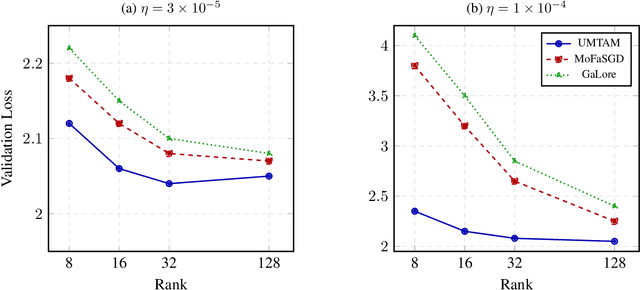
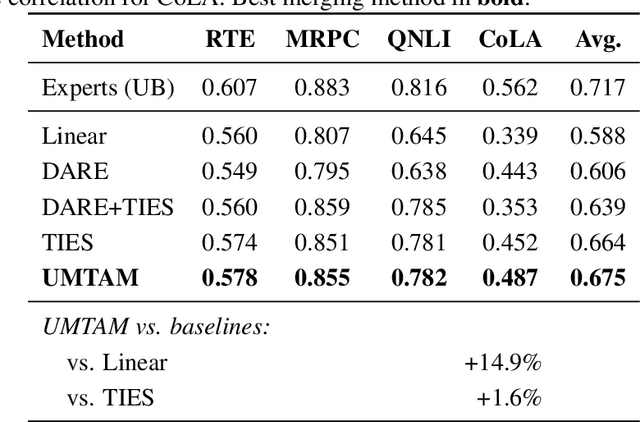
Training large neural networks and merging task-specific models both exploit low-rank structure and require parameter importance estimation, yet these challenges have been pursued in isolation. Current workflows compute curvature information during training, discard it, then recompute similar information for merging -- wasting computation and discarding valuable trajectory data. We introduce a unified framework that maintains factorized momentum and curvature statistics during training, then reuses this information for geometry-aware model composition. The proposed method achieves memory efficiency comparable to state-of-the-art approaches while accumulating task saliency scores that enable curvature-aware merging without post-hoc Fisher computation. We establish convergence guarantees for non-convex objectives with approximation error bounded by gradient singular value decay. On natural language understanding benchmarks, curvature-aware parameter selection outperforms magnitude-only baselines across all sparsity levels, with multi-task merging improving over strong baselines. The proposed framework exhibits rank-invariant convergence and superior hyperparameter robustness compared to existing low-rank optimizers. By treating the optimization trajectory as a reusable asset rather than discarding it, our approach eliminates redundant computation while enabling more principled model composition.

Time series clustering based on the characterisation of segment typologies

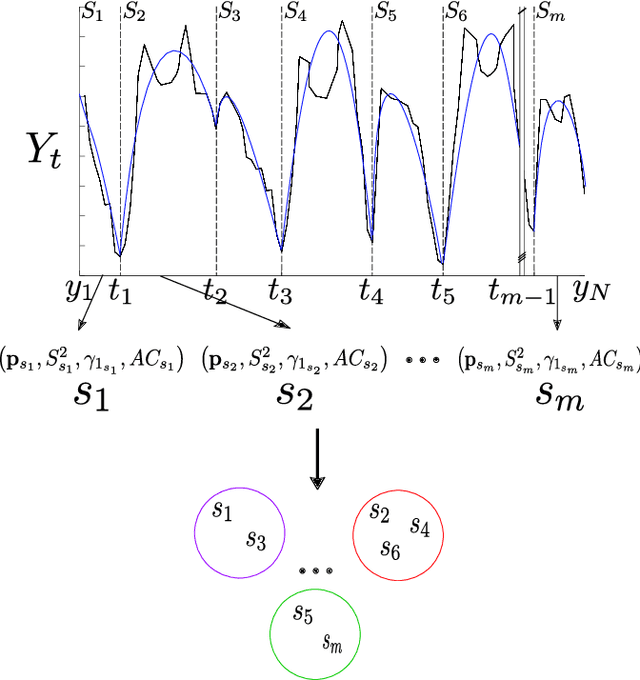
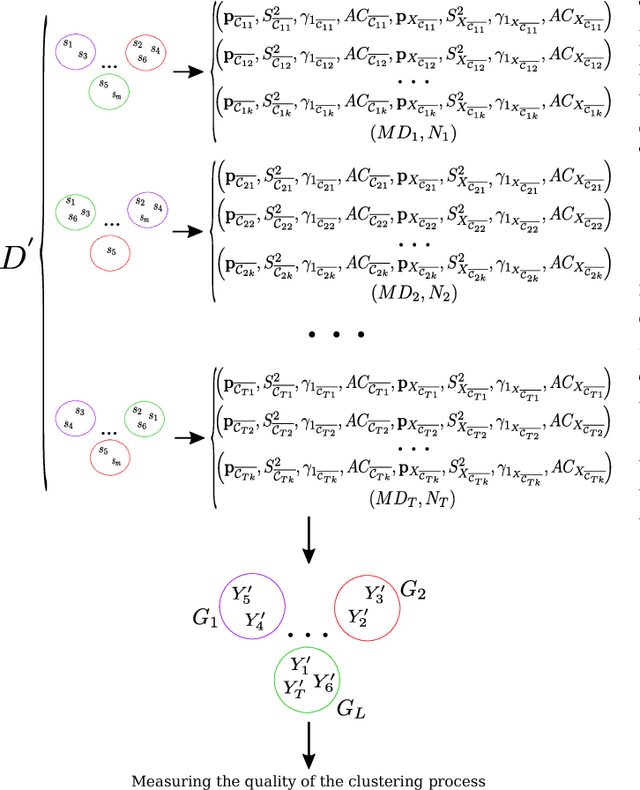
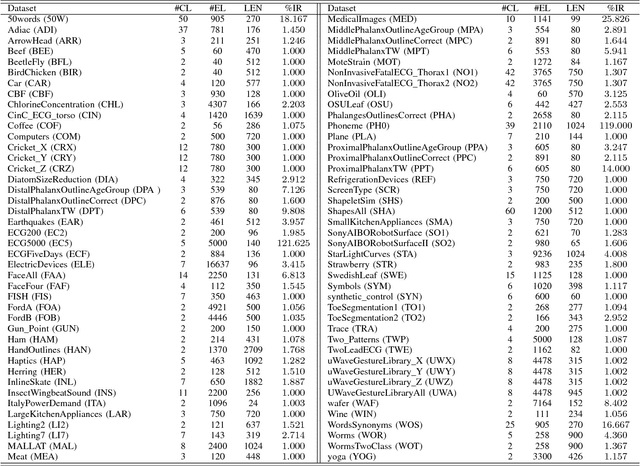
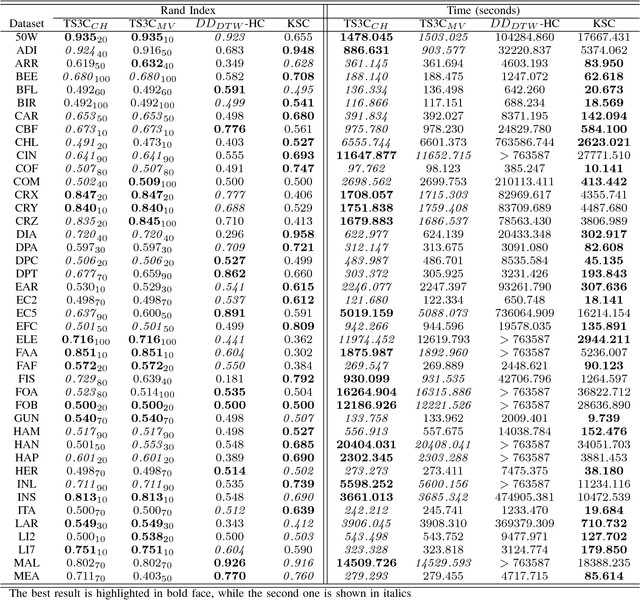
Time series clustering is the process of grouping time series with respect to their similarity or characteristics. Previous approaches usually combine a specific distance measure for time series and a standard clustering method. However, these approaches do not take the similarity of the different subsequences of each time series into account, which can be used to better compare the time series objects of the dataset. In this paper, we propose a novel technique of time series clustering based on two clustering stages. In a first step, a least squares polynomial segmentation procedure is applied to each time series, which is based on a growing window technique that returns different-length segments. Then, all the segments are projected into same dimensional space, based on the coefficients of the model that approximates the segment and a set of statistical features. After mapping, a first hierarchical clustering phase is applied to all mapped segments, returning groups of segments for each time series. These clusters are used to represent all time series in the same dimensional space, after defining another specific mapping process. In a second and final clustering stage, all the time series objects are grouped. We consider internal clustering quality to automatically adjust the main parameter of the algorithm, which is an error threshold for the segmenta- tion. The results obtained on 84 datasets from the UCR Time Series Classification Archive have been compared against two state-of-the-art methods, showing that the performance of this methodology is very promising.