qc-kmeans: A Quantum Compressive K-Means Algorithm for NISQ Devices

Clustering on NISQ hardware is constrained by data loading and limited qubits. We present \textbf{qc-kmeans}, a hybrid compressive $k$-means that summarizes a dataset with a constant-size Fourier-feature sketch and selects centroids by solving small per-group QUBOs with shallow QAOA circuits. The QFF sketch estimator is unbiased with mean-squared error $O(\varepsilon^2)$ for $B,S=\Theta(\varepsilon^{-2})$, and the peak-qubit requirement $q_{\text{peak}}=\max\{D,\lceil \log_2 B\rceil + 1\}$ does not scale with the number of samples. A refinement step with elitist retention ensures non-increasing surrogate cost. In Qiskit Aer simulations (depth $p{=}1$), the method ran with $\le 9$ qubits on low-dimensional synthetic benchmarks and achieved competitive sum-of-squared errors relative to quantum baselines; runtimes are not directly comparable. On nine real datasets (up to $4.3\times 10^5$ points), the pipeline maintained constant peak-qubit usage in simulation. Under IBM noise models, accuracy was similar to the idealized setting. Overall, qc-kmeans offers a NISQ-oriented formulation with shallow, bounded-width circuits and competitive clustering quality in simulation.

A Scalable Global Optimization Algorithm For Constrained Clustering

Constrained clustering leverages limited domain knowledge to improve clustering performance and interpretability, but incorporating pairwise must-link and cannot-link constraints is an NP-hard challenge, making global optimization intractable. Existing mixed-integer optimization methods are confined to small-scale datasets, limiting their utility. We propose Sample-Driven Constrained Group-Based Branch-and-Bound (SDC-GBB), a decomposable branch-and-bound (BB) framework that collapses must-linked samples into centroid-based pseudo-samples and prunes cannot-link through geometric rules, while preserving convergence and guaranteeing global optimality. By integrating grouped-sample Lagrangian decomposition and geometric elimination rules for efficient lower and upper bounds, the algorithm attains highly scalable pairwise k-Means constrained clustering via parallelism. Experimental results show that our approach handles datasets with 200,000 samples with cannot-link constraints and 1,500,000 samples with must-link constraints, which is 200 - 1500 times larger than the current state-of-the-art under comparable constraint settings, while reaching an optimality gap of less than 3%. In providing deterministic global guarantees, our method also avoids the search failures that off-the-shelf heuristics often encounter on large datasets.

SPOT: Scalable Policy Optimization with Trees for Markov Decision Processes

Interpretable reinforcement learning policies are essential for high-stakes decision-making, yet optimizing decision tree policies in Markov Decision Processes (MDPs) remains challenging. We propose SPOT, a novel method for computing decision tree policies, which formulates the optimization problem as a mixed-integer linear program (MILP). To enhance efficiency, we employ a reduced-space branch-and-bound approach that decouples the MDP dynamics from tree-structure constraints, enabling efficient parallel search. This significantly improves runtime and scalability compared to previous methods. Our approach ensures that each iteration yields the optimal decision tree. Experimental results on standard benchmarks demonstrate that SPOT achieves substantial speedup and scales to larger MDPs with a significantly higher number of states. The resulting decision tree policies are interpretable and compact, maintaining transparency without compromising performance. These results demonstrate that our approach simultaneously achieves interpretability and scalability, delivering high-quality policies an order of magnitude faster than existing approaches.

A GPU-Accelerated Moving-Horizon Algorithm for Training Deep Classification Trees on Large Datasets

Decision trees are essential yet NP-complete to train, prompting the widespread use of heuristic methods such as CART, which suffers from sub-optimal performance due to its greedy nature. Recently, breakthroughs in finding optimal decision trees have emerged; however, these methods still face significant computational costs and struggle with continuous features in large-scale datasets and deep trees. To address these limitations, we introduce a moving-horizon differential evolution algorithm for classification trees with continuous features (MH-DEOCT). Our approach consists of a discrete tree decoding method that eliminates duplicated searches between adjacent samples, a GPU-accelerated implementation that significantly reduces running time, and a moving-horizon strategy that iteratively trains shallow subtrees at each node to balance the vision and optimizer capability. Comprehensive studies on 68 UCI datasets demonstrate that our approach outperforms the heuristic method CART on training and testing accuracy by an average of 3.44% and 1.71%, respectively. Moreover, these numerical studies empirically demonstrate that MH-DEOCT achieves near-optimal performance (only 0.38% and 0.06% worse than the global optimal method on training and testing, respectively), while it offers remarkable scalability for deep trees (e.g., depth=8) and large-scale datasets (e.g., ten million samples).

Multilingual Lexical Simplification via Paraphrase Generation

Lexical simplification (LS) methods based on pretrained language models have made remarkable progress, generating potential substitutes for a complex word through analysis of its contextual surroundings. However, these methods require separate pretrained models for different languages and disregard the preservation of sentence meaning. In this paper, we propose a novel multilingual LS method via paraphrase generation, as paraphrases provide diversity in word selection while preserving the sentence's meaning. We regard paraphrasing as a zero-shot translation task within multilingual neural machine translation that supports hundreds of languages. After feeding the input sentence into the encoder of paraphrase modeling, we generate the substitutes based on a novel decoding strategy that concentrates solely on the lexical variations of the complex word. Experimental results demonstrate that our approach surpasses BERT-based methods and zero-shot GPT3-based method significantly on English, Spanish, and Portuguese.

A Global Optimization Algorithm for K-Center Clustering of One Billion Samples

This paper presents a practical global optimization algorithm for the K-center clustering problem, which aims to select K samples as the cluster centers to minimize the maximum within-cluster distance. This algorithm is based on a reduced-space branch and bound scheme and guarantees convergence to the global optimum in a finite number of steps by only branching on the regions of centers. To improve efficiency, we have designed a two-stage decomposable lower bound, the solution of which can be derived in a closed form. In addition, we also propose several acceleration techniques to narrow down the region of centers, including bounds tightening, sample reduction, and parallelization. Extensive studies on synthetic and real-world datasets have demonstrated that our algorithm can solve the K-center problems to global optimal within 4 hours for ten million samples in the serial mode and one billion samples in the parallel mode. Moreover, compared with the state-of-the-art heuristic methods, the global optimum obtained by our algorithm can averagely reduce the objective function by 25.8% on all the synthetic and real-world datasets.

Data ultrametricity and clusterability

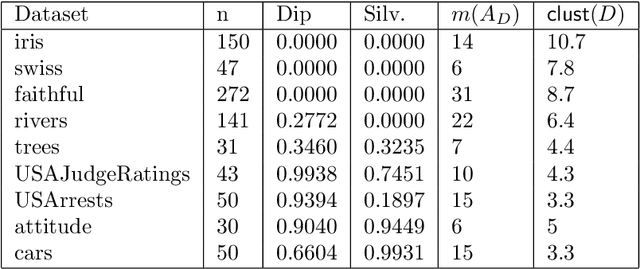
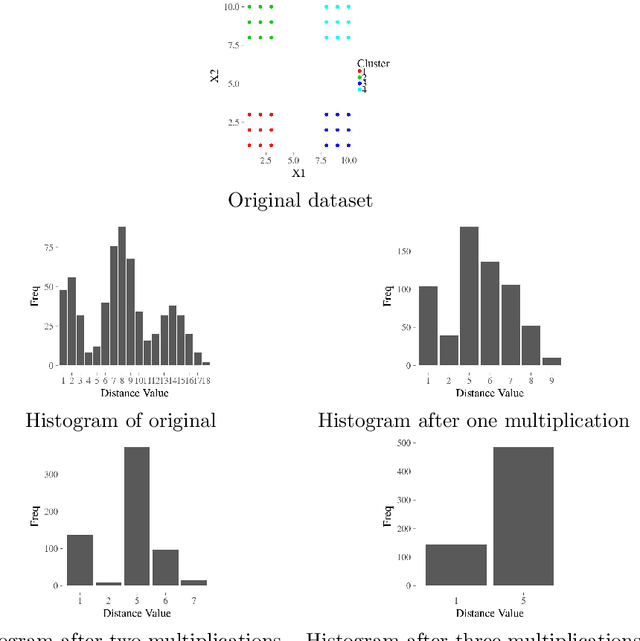
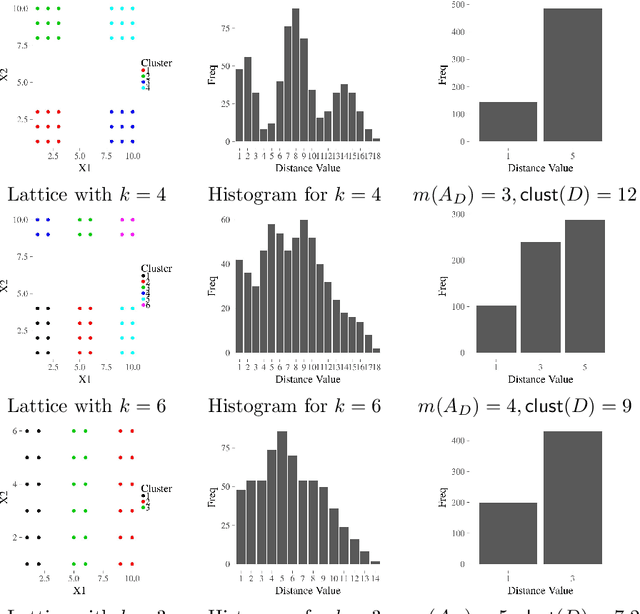
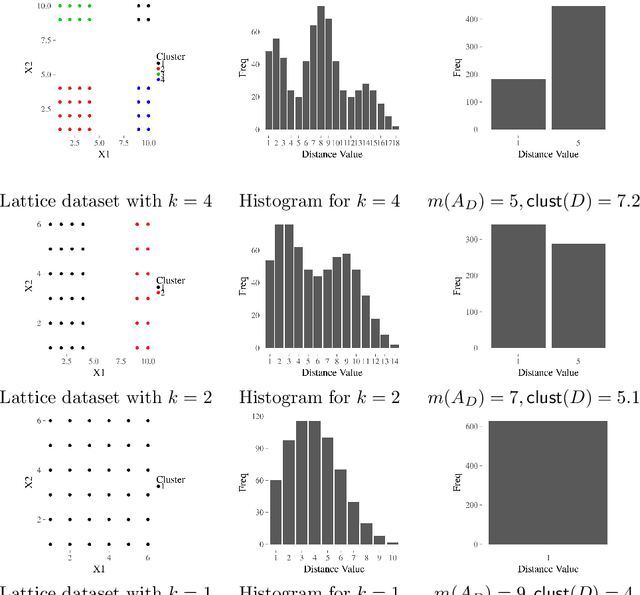
The increasing needs of clustering massive datasets and the high cost of running clustering algorithms poses difficult problems for users. In this context it is important to determine if a data set is clusterable, that is, it may be partitioned efficiently into well-differentiated groups containing similar objects. We approach data clusterability from an ultrametric-based perspective. A novel approach to determine the ultrametricity of a dataset is proposed via a special type of matrix product, which allows us to evaluate the clusterability of the dataset. Furthermore, we show that by applying our technique to a dissimilarity space will generate the sub-dominant ultrametric of the dissimilarity.