Object Discovery in Videos as Foreground Motion Clustering

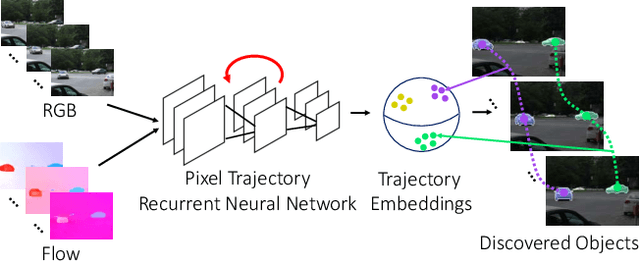
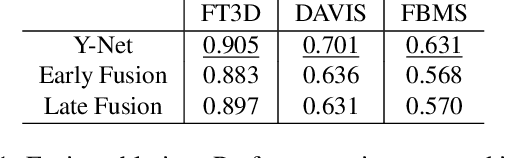
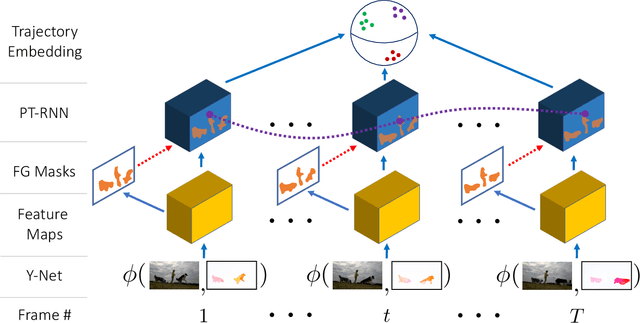
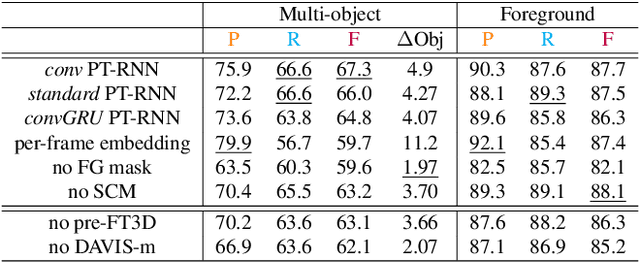
We consider the problem of providing dense segmentation masks for object discovery in videos. We formulate the object discovery problem as foreground motion clustering, where the goal is to cluster foreground pixels in videos into different objects. We introduce a novel pixel-trajectory recurrent neural network that learns feature embeddings of foreground pixel trajectories linked in time. By clustering the pixel trajectories using the learned feature embeddings, our method establishes correspondences between foreground object masks across video frames. To demonstrate the effectiveness of our framework for object discovery, we conduct experiments on commonly used datasets for motion segmentation, where we achieve state-of-the-art performance.

Coupled Recurrent Models for Polyphonic Music Composition

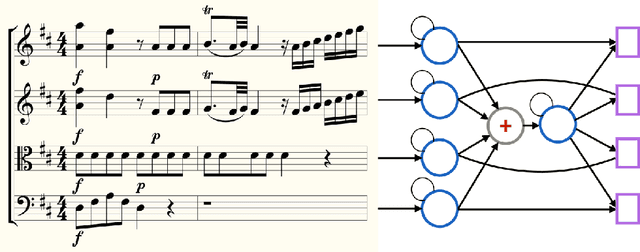
This work describes a novel recurrent model for music composition, which accounts for the rich statistical structure of polyphonic music. There are many ways to factor the probability distribution over musical scores; we consider the merits of various approaches and propose a new factorization that decomposes a score into a collection of concurrent, coupled time series: 'parts.' The model we propose borrows ideas from both convolutional neural models and recurrent neural models; we argue that these ideas are natural for capturing music's pitch invariances, temporal structure, and polyphony. We train generative models for homophonic and polyphonic composition on the KernScores dataset (Sapp, 2005) a collection of 2,300 musical scores comprised of around 2.8 million notes spanning time from the Renaissance to the early 20th century. While evaluation of generative models is known to be hard (Theis et al., 2016), we present careful quantitative results using a unit-adjusted cross entropy metric that is independent of how we factor the distribution over scores. We also present qualitative results using a blind discrimination test.

An Inexact Variable Metric Proximal Point Algorithm for Generic Quasi-Newton Acceleration

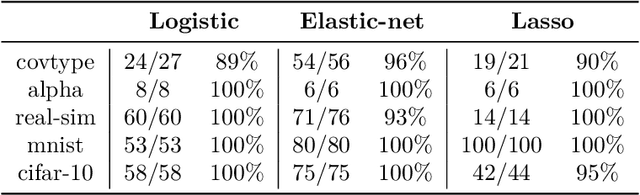
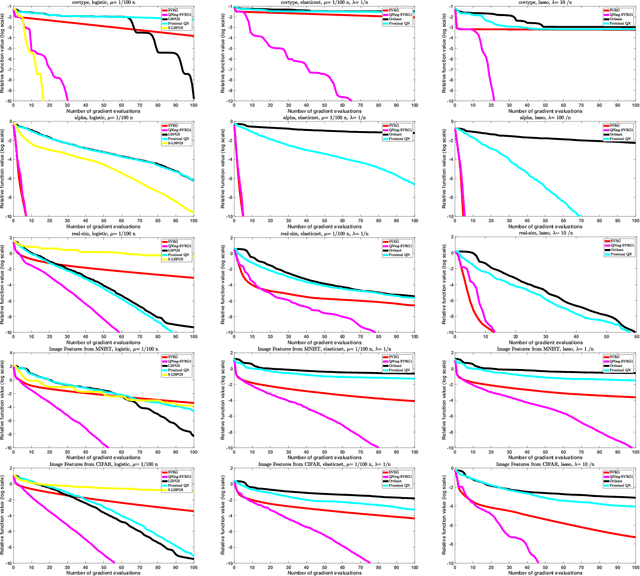
We propose an inexact variable-metric proximal point algorithm to accelerate gradient-based optimization algorithms. The proposed scheme, called QNing can be notably applied to incremental first-order methods such as the stochastic variance-reduced gradient descent algorithm (SVRG) and other randomized incremental optimization algorithms. QNing is also compatible with composite objectives, meaning that it has the ability to provide exactly sparse solutions when the objective involves a sparsity-inducing regularization. When combined with limited-memory BFGS rules, QNing is particularly effective to solve high-dimensional optimization problems, while enjoying a worst-case linear convergence rate for strongly convex problems. We present experimental results where QNing gives significant improvements over competing methods for training machine learning methods on large samples and in high dimensions.

Catalyst Acceleration for First-order Convex Optimization: from Theory to Practice

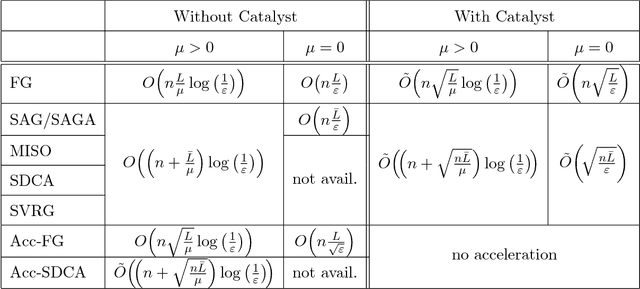
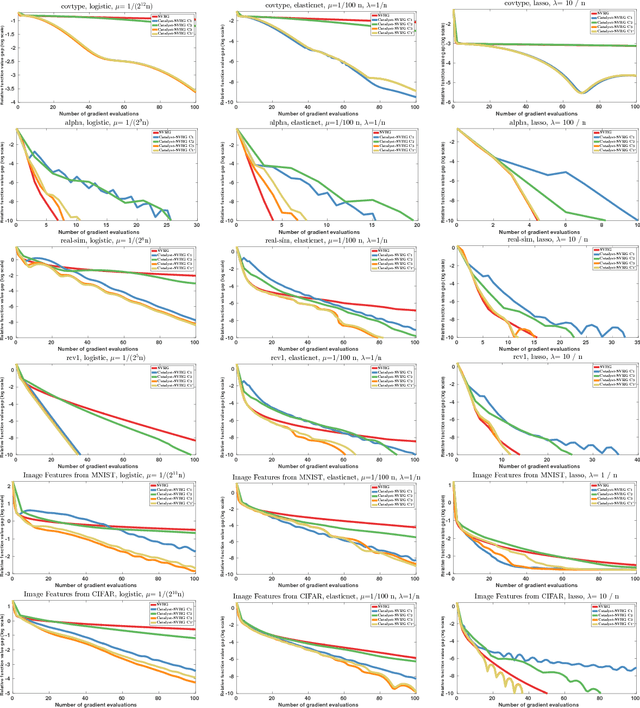
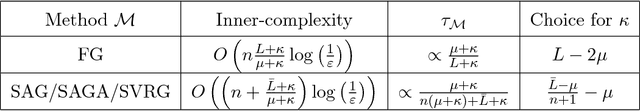
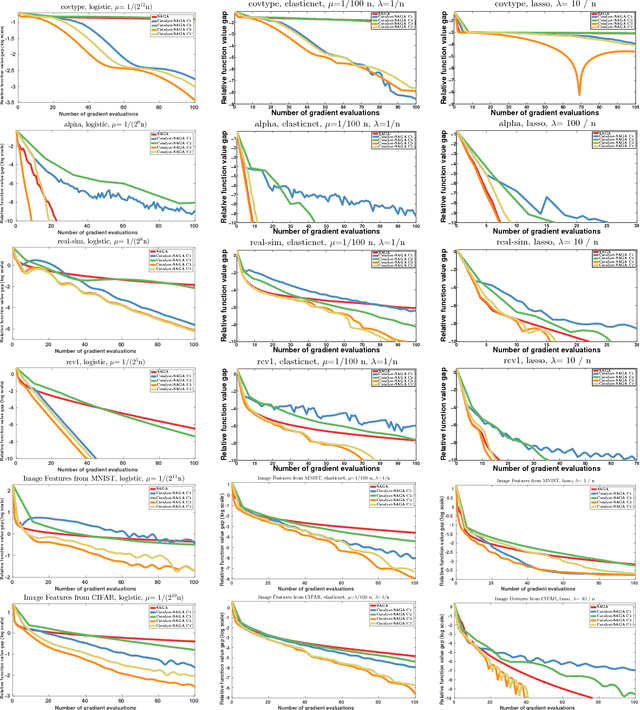
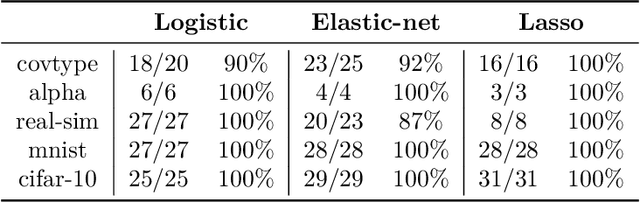
We introduce a generic scheme for accelerating gradient-based optimization methods in the sense of Nesterov. The approach, called Catalyst, builds upon the inexact accelerated proximal point algorithm for minimizing a convex objective function, and consists of approximately solving a sequence of well-chosen auxiliary problems, leading to faster convergence. One of the keys to achieve acceleration in theory and in practice is to solve these sub-problems with appropriate accuracy by using the right stopping criterion and the right warm-start strategy. We give practical guidelines to use Catalyst and present a comprehensive analysis of its global complexity. We show that Catalyst applies to a large class of algorithms, including gradient descent, block coordinate descent, incremental algorithms such as SAG, SAGA, SDCA, SVRG, MISO/Finito, and their proximal variants. For all of these methods, we establish faster rates using the Catalyst acceleration, for strongly convex and non-strongly convex objectives. We conclude with extensive experiments showing that acceleration is useful in practice, especially for ill-conditioned problems.

Efficient First-Order Algorithms for Adaptive Signal Denoising

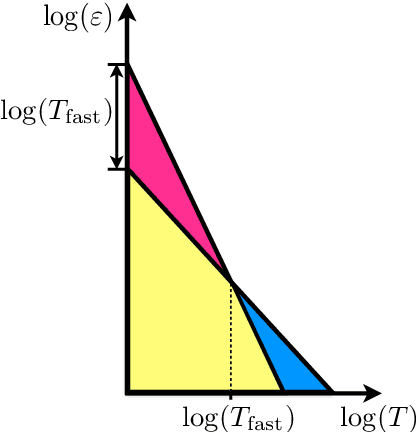
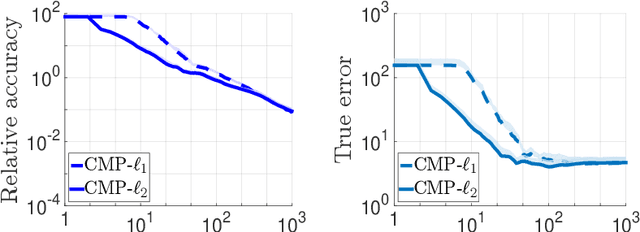
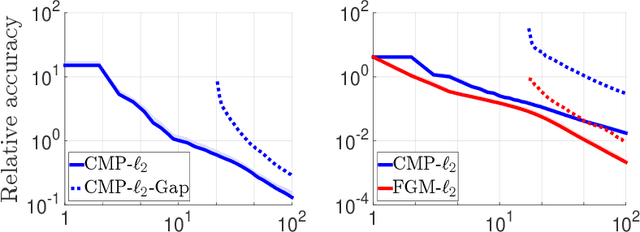
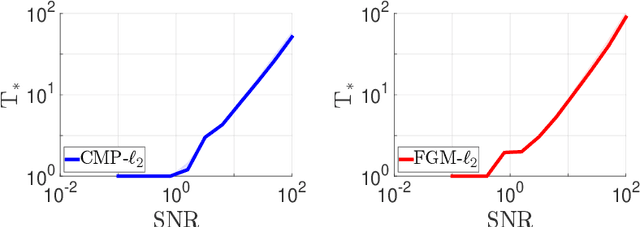
We consider the problem of discrete-time signal denoising, focusing on a specific family of non-linear convolution-type estimators. Each such estimator is associated with a time-invariant filter which is obtained adaptively, by solving a certain convex optimization problem. Adaptive convolution-type estimators were demonstrated to have favorable statistical properties. However, the question of their computational complexity remains largely unexplored, and in fact we are not aware of any publicly available implementation of these estimators. Our first contribution is an efficient implementation of these estimators via some known first-order proximal algorithms. Our second contribution is a computational complexity analysis of the proposed procedures, which takes into account their statistical nature and the related notion of statistical accuracy. The proposed procedures and their analysis are illustrated on a simulated data benchmark.

Adaptive Denoising of Signals with Shift-Invariant Structure

We study the problem of discrete-time signal denoising, following the line of research initiated by [Nem91] and further developed in [JN09, JN10, HJNO15, OHJN16]. Previous papers considered the following setup: the signal is assumed to admit a convolution-type linear oracle -- an unknown linear estimator in the form of the convolution of the observations with an unknown time-invariant filter with small $\ell_2$-norm. It was shown that such an oracle can be "mimicked" by an efficiently computable non-linear convolution-type estimator, in which the filter minimizes the Fourier-domain $\ell_\infty$-norm of the residual, regularized by the Fourier-domain $\ell_1$-norm of the filter. Following [OHJN16], here we study an alternative family of estimators, replacing the $\ell_\infty$-norm of the residual with the $\ell_2$-norm. Such estimators are found to have better statistical properties, in particular, we prove sharp oracle inequalities for their $\ell_2$-loss. Our guarantees require an extra assumption of approximate shift-invariance: the signal must be $\varkappa$-close, in $\ell_2$-metric, to some shift-invariant linear subspace with bounded dimension $s$. However, this subspace can be completely unknown, and the remainder terms in the oracle inequalities scale at most polynomially with $s$ and $\varkappa$. In conclusion, we show that the new assumption implies the previously considered one, providing explicit constructions of the convolution-type linear oracles with $\ell_2$-norm bounded in terms of parameters $s$ and $\varkappa$.

Rademacher Complexity Bounds for a Penalized Multiclass Semi-Supervised Algorithm

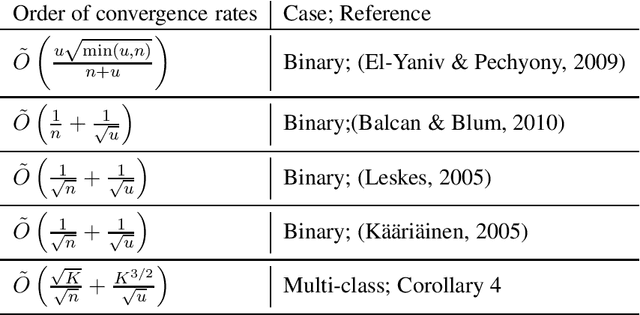
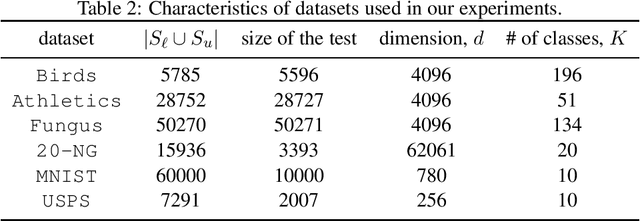
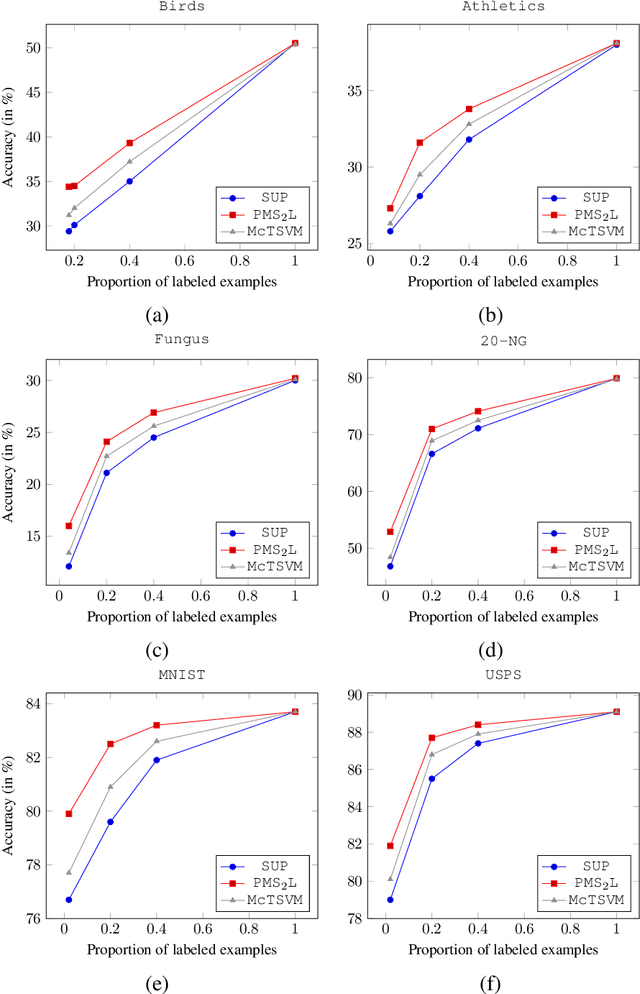
We propose Rademacher complexity bounds for multiclass classifiers trained with a two-step semi-supervised model. In the first step, the algorithm partitions the partially labeled data and then identifies dense clusters containing $\kappa$ predominant classes using the labeled training examples such that the proportion of their non-predominant classes is below a fixed threshold. In the second step, a classifier is trained by minimizing a margin empirical loss over the labeled training set and a penalization term measuring the disability of the learner to predict the $\kappa$ predominant classes of the identified clusters. The resulting data-dependent generalization error bound involves the margin distribution of the classifier, the stability of the clustering technique used in the first step and Rademacher complexity terms corresponding to partially labeled training data. Our theoretical result exhibit convergence rates extending those proposed in the literature for the binary case, and experimental results on different multiclass classification problems show empirical evidence that supports the theory.

Invariances and Data Augmentation for Supervised Music Transcription

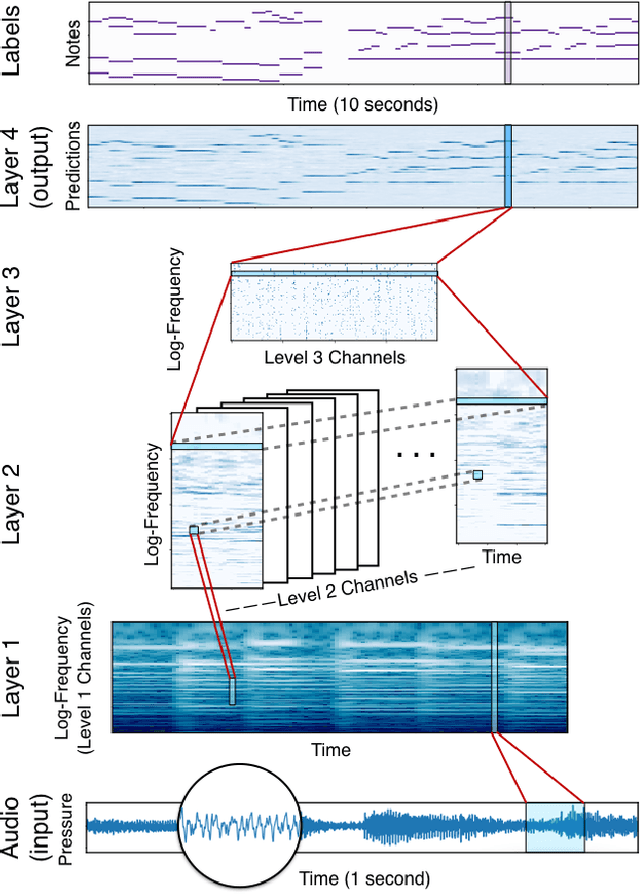
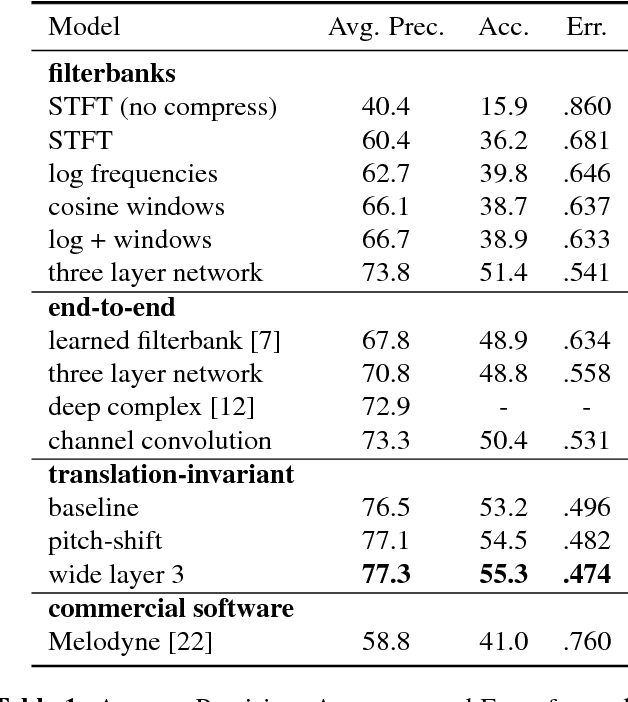
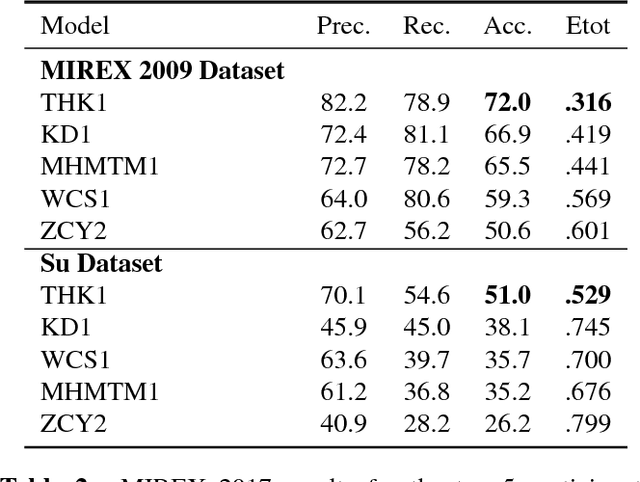
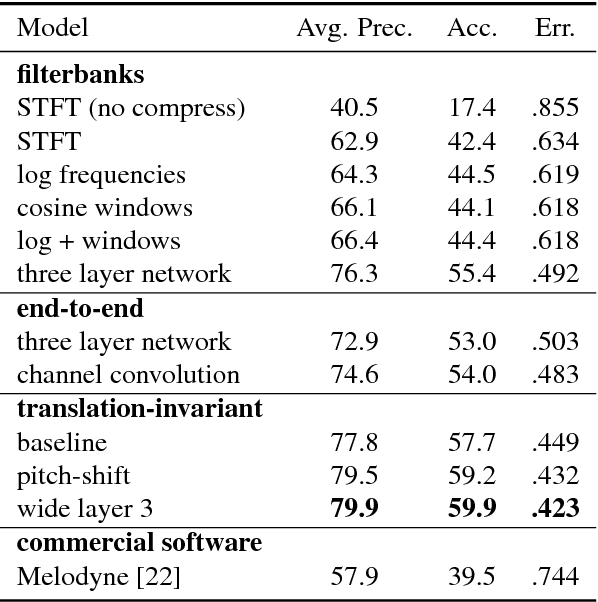
This paper explores a variety of models for frame-based music transcription, with an emphasis on the methods needed to reach state-of-the-art on human recordings. The translation-invariant network discussed in this paper, which combines a traditional filterbank with a convolutional neural network, was the top-performing model in the 2017 MIREX Multiple Fundamental Frequency Estimation evaluation. This class of models shares parameters in the log-frequency domain, which exploits the frequency invariance of music to reduce the number of model parameters and avoid overfitting to the training data. All models in this paper were trained with supervision by labeled data from the MusicNet dataset, augmented by random label-preserving pitch-shift transformations.

Catalyst Acceleration for Gradient-Based Non-Convex Optimization

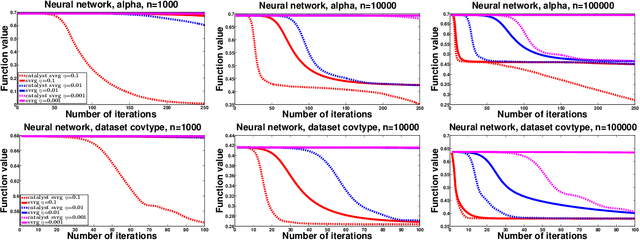
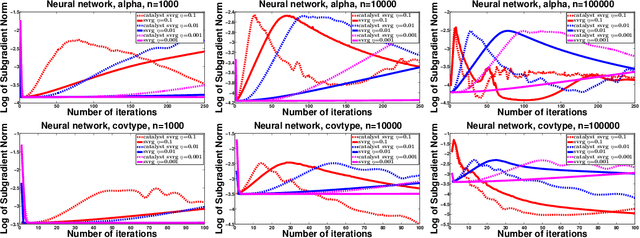
We introduce a generic scheme to solve nonconvex optimization problems using gradient-based algorithms originally designed for minimizing convex functions. When the objective is convex, the proposed approach enjoys the same properties as the Catalyst approach of Lin et al. [22]. When the objective is nonconvex, it achieves the best known convergence rate to stationary points for first-order methods. Specifically, the proposed algorithm does not require knowledge about the convexity of the objective; yet, it obtains an overall worst-case efficiency of $\tilde{O}(\varepsilon^{-2})$ and, if the function is convex, the complexity reduces to the near-optimal rate $\tilde{O}(\varepsilon^{-2/3})$. We conclude the paper by showing promising experimental results obtained by applying the proposed approach to SVRG and SAGA for sparse matrix factorization and for learning neural networks.

Learning Features of Music from Scratch

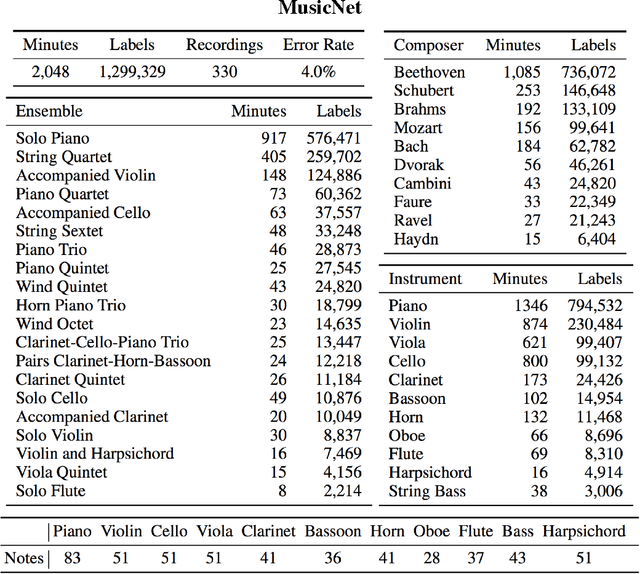
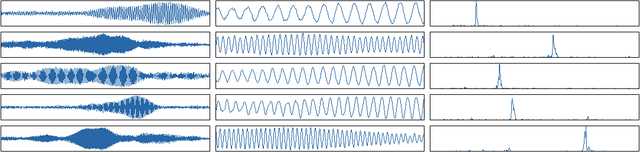
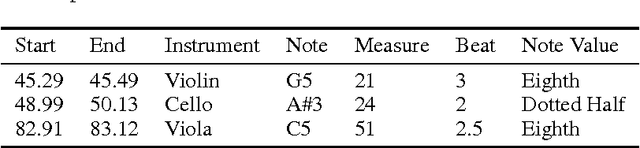
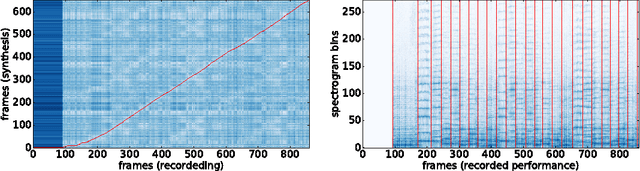
This paper introduces a new large-scale music dataset, MusicNet, to serve as a source of supervision and evaluation of machine learning methods for music research. MusicNet consists of hundreds of freely-licensed classical music recordings by 10 composers, written for 11 instruments, together with instrument/note annotations resulting in over 1 million temporal labels on 34 hours of chamber music performances under various studio and microphone conditions. The paper defines a multi-label classification task to predict notes in musical recordings, along with an evaluation protocol, and benchmarks several machine learning architectures for this task: i) learning from spectrogram features; ii) end-to-end learning with a neural net; iii) end-to-end learning with a convolutional neural net. These experiments show that end-to-end models trained for note prediction learn frequency selective filters as a low-level representation of audio.