Harmonic Decompositions of Convolutional Networks

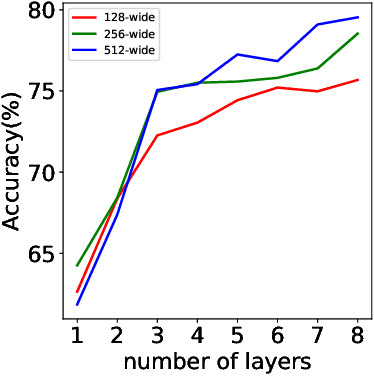
We consider convolutional networks from a reproducing kernel Hilbert space viewpoint. We establish harmonic decompositions of convolutional networks, that is expansions into sums of elementary functions of increasing order. The elementary functions are related to the spherical harmonics, a fundamental class of special functions on spheres. The harmonic decompositions allow us to characterize the integral operators associated with convolutional networks, and obtain as a result statistical bounds for convolutional networks.

Risk Bounds for Multi-layer Perceptrons through Spectra of Integral Operators

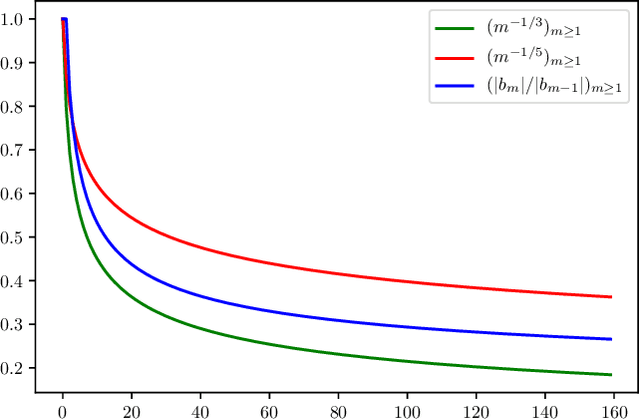
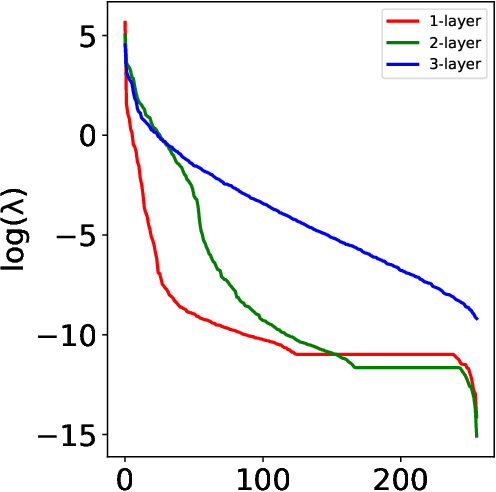
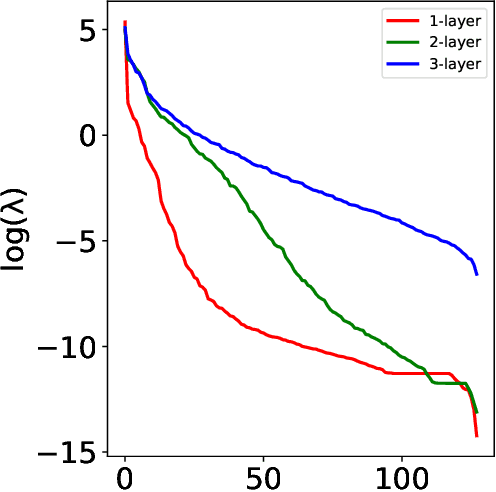
We characterize the behavior of integral operators associated with multi-layer perceptrons in two eigenvalue decay regimes. We obtain as a result sharper risk bounds for multi-layer perceptrons highlighting their behavior in high dimensions. Doing so, we also improve on previous results on integral operators related to power series kernels on spheres, with sharper eigenvalue decay estimates in a wider range of eigenvalue decay regimes.

Device Heterogeneity in Federated Learning: A Superquantile Approach

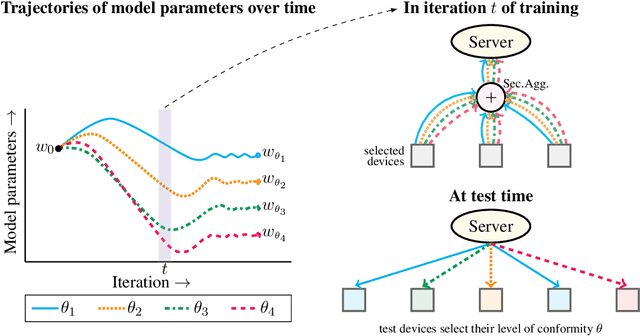
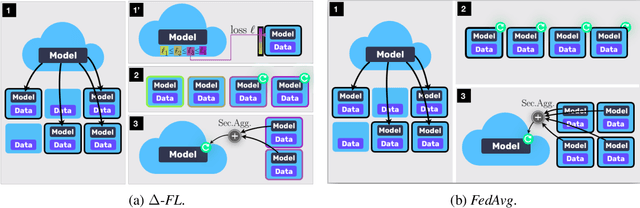
We propose a federated learning framework to handle heterogeneous client devices which do not conform to the population data distribution. The approach hinges upon a parameterized superquantile-based objective, where the parameter ranges over levels of conformity. We present an optimization algorithm and establish its convergence to a stationary point. We show how to practically implement it using secure aggregation by interleaving iterations of the usual federated averaging method with device filtering. We conclude with numerical experiments on neural networks as well as linear models on tasks from computer vision and natural language processing.

An Elementary Approach to Convergence Guarantees of Optimization Algorithms for Deep Networks

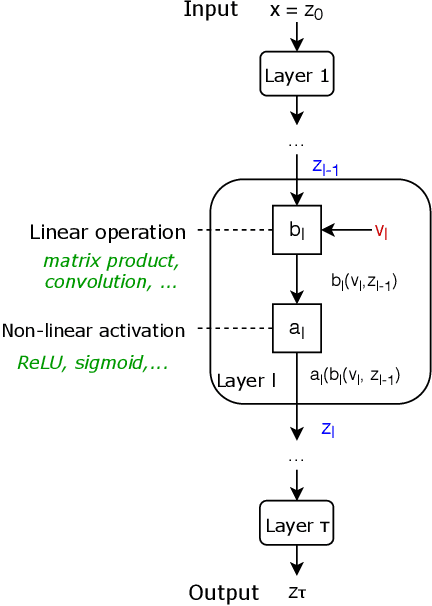
We present an approach to obtain convergence guarantees of optimization algorithms for deep networks based on elementary arguments and computations. The convergence analysis revolves around the analytical and computational structures of optimization oracles central to the implementation of deep networks in machine learning software. We provide a systematic way to compute estimates of the smoothness constants that govern the convergence behavior of first-order optimization algorithms used to train deep networks. A diverse set of example components and architectures arising in modern deep networks intersperse the exposition to illustrate the approach.

Robust Aggregation for Federated Learning

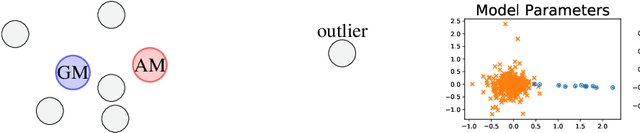
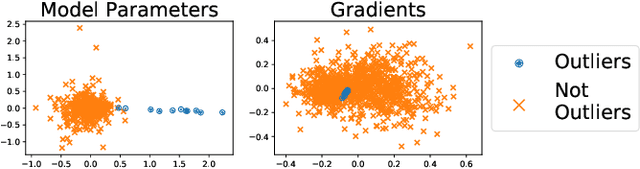
We present a robust aggregation approach to make federated learning robust to settings when a fraction of the devices may be sending corrupted updates to the server. The proposed approach relies on a robust secure aggregation oracle based on the geometric median, which returns a robust aggregate using a constant number of calls to a regular non-robust secure average oracle. The robust aggregation oracle is privacy-preserving, similar to the secure average oracle it builds upon. We provide experimental results of the proposed approach with linear models and deep networks for two tasks in computer vision and natural language processing. The robust aggregation approach is agnostic to the level of corruption; it outperforms the classical aggregation approach in terms of robustness when the level of corruption is high, while being competitive in the regime of low corruption.

End-to-end Learning, with or without Labels

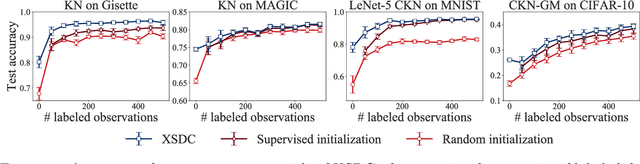
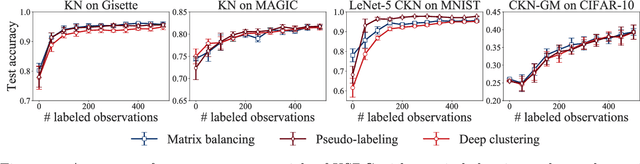
We present an approach for end-to-end learning that allows one to jointly learn a feature representation from unlabeled data (with or without labeled data) and predict labels for unlabeled data. The feature representation is assumed to be specified in a differentiable programming framework, that is, as a parameterized mapping amenable to automatic differentiation. The proposed approach can be used with any amount of labeled and unlabeled data, gracefully adjusting to the amount of supervision. We provide experimental results illustrating the effectiveness of the approach.

Advances and Open Problems in Federated Learning

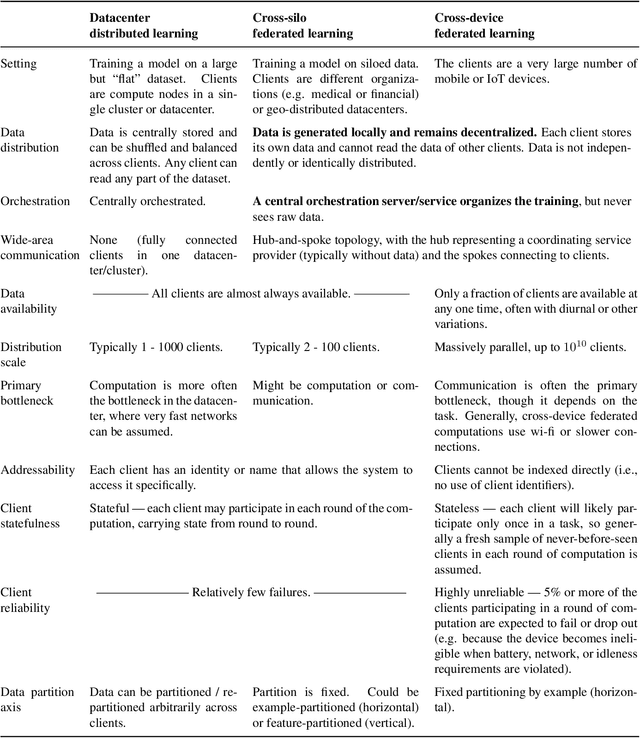
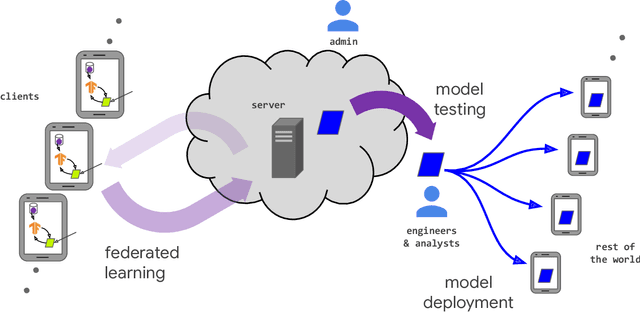
Federated learning (FL) is a machine learning setting where many clients (e.g. mobile devices or whole organizations) collaboratively train a model under the orchestration of a central server (e.g. service provider), while keeping the training data decentralized. FL embodies the principles of focused data collection and minimization, and can mitigate many of the systemic privacy risks and costs resulting from traditional, centralized machine learning and data science approaches. Motivated by the explosive growth in FL research, this paper discusses recent advances and presents an extensive collection of open problems and challenges.

A Statistical Investigation of Long Memory in Language and Music

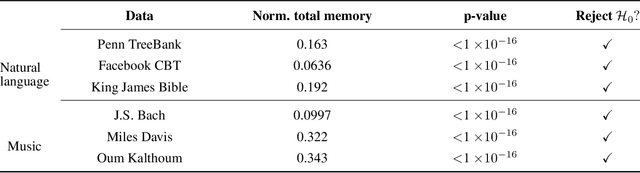
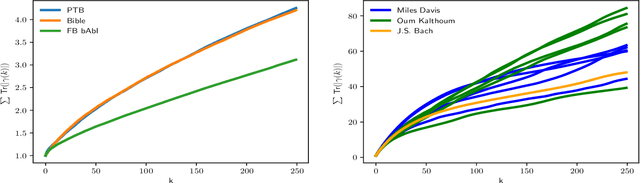
Representation and learning of long-range dependencies is a central challenge confronted in modern applications of machine learning to sequence data. Yet despite the prominence of this issue, the basic problem of measuring long-range dependence, either in a given data source or as represented in a trained deep model, remains largely limited to heuristic tools. We contribute a statistical framework for investigating long-range dependence in current applications of sequence modeling, drawing on the statistical theory of long memory stochastic processes. By analogy with their linear predecessors in the time series literature, we identify recurrent neural networks (RNNs) as nonlinear processes that simultaneously attempt to learn both a feature representation for and the long-range dependency structure of an input sequence. We derive testable implications concerning the relationship between long memory in real-world data and its learned representation in a deep network architecture, which are explored through a semiparametric framework adapted to the high-dimensional setting. We establish the validity of statistical inference for a simple estimator, which yields a decision rule for long memory in RNNs. Experiments illustrating this statistical framework confirm the presence of long memory in a diverse collection of natural language and music data, but show that a variety of RNN architectures fail to capture this property even after training to benchmark accuracy in a language model.

Kernel-based Translations of Convolutional Networks

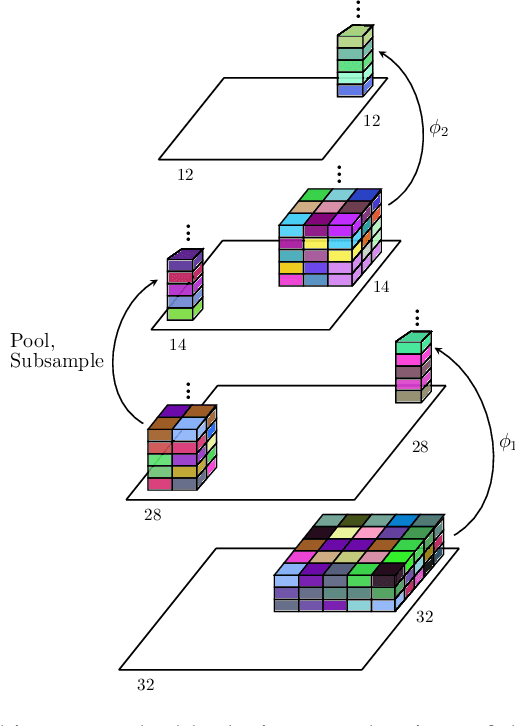
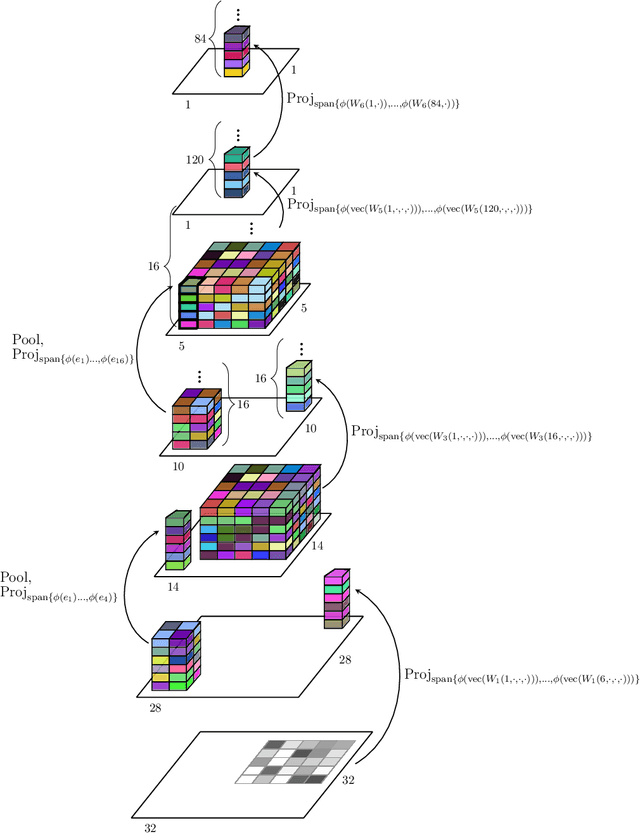
Convolutional Neural Networks, as most artificial neural networks, are commonly viewed as methods different in essence from kernel-based methods. We provide a systematic translation of Convolutional Neural Networks (ConvNets) into their kernel-based counterparts, Convolutional Kernel Networks (CKNs), and demonstrate that this perception is unfounded both formally and empirically. We show that, given a Convolutional Neural Network, we can design a corresponding Convolutional Kernel Network, easily trainable using a new stochastic gradient algorithm based on an accurate gradient computation, that performs on par with its Convolutional Neural Network counterpart. We present experimental results supporting our claims on landmark ConvNet architectures comparing each ConvNet to its CKN counterpart over several parameter settings.

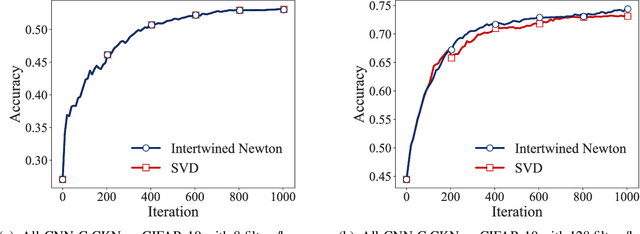
A Smoother Way to Train Structured Prediction Models

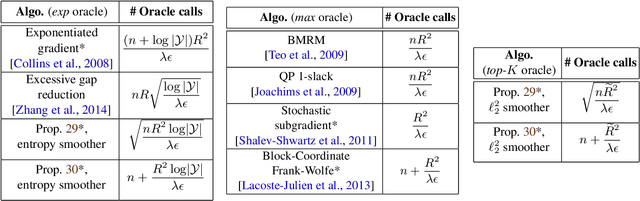
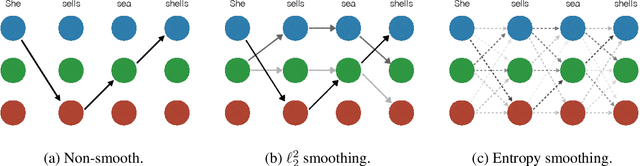
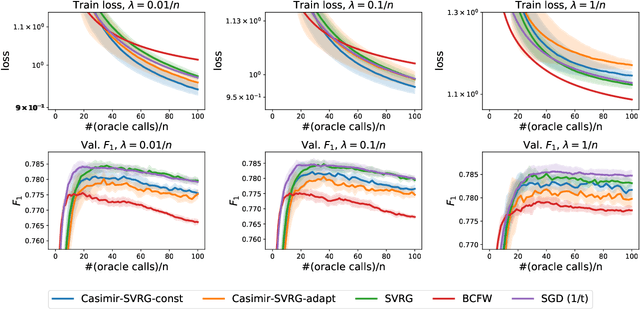
We present a framework to train a structured prediction model by performing smoothing on the inference algorithm it builds upon. Smoothing overcomes the non-smoothness inherent to the maximum margin structured prediction objective, and paves the way for the use of fast primal gradient-based optimization algorithms. We illustrate the proposed framework by developing a novel primal incremental optimization algorithm for the structural support vector machine. The proposed algorithm blends an extrapolation scheme for acceleration and an adaptive smoothing scheme and builds upon the stochastic variance-reduced gradient algorithm. We establish its worst-case global complexity bound and study several practical variants, including extensions to deep structured prediction. We present experimental results on two real-world problems, namely named entity recognition and visual object localization. The experimental results show that the proposed framework allows us to build upon efficient inference algorithms to develop large-scale optimization algorithms for structured prediction which can achieve competitive performance on the two real-world problems.