Rachel Cummings
Beyond Laplace and Gaussian: Exploring the Generalized Gaussian Mechanism for Private Machine Learning
Jun 14, 2025Abstract:Differential privacy (DP) is obtained by randomizing a data analysis algorithm, which necessarily introduces a tradeoff between its utility and privacy. Many DP mechanisms are built upon one of two underlying tools: Laplace and Gaussian additive noise mechanisms. We expand the search space of algorithms by investigating the Generalized Gaussian mechanism, which samples the additive noise term $x$ with probability proportional to $e^{-\frac{| x |}{\sigma}^{\beta} }$ for some $\beta \geq 1$. The Laplace and Gaussian mechanisms are special cases of GG for $\beta=1$ and $\beta=2$, respectively. In this work, we prove that all members of the GG family satisfy differential privacy, and provide an extension of an existing numerical accountant (the PRV accountant) for these mechanisms. We show that privacy accounting for the GG Mechanism and its variants is dimension independent, which substantially improves computational costs of privacy accounting. We apply the GG mechanism to two canonical tools for private machine learning, PATE and DP-SGD; we show empirically that $\beta$ has a weak relationship with test-accuracy, and that generally $\beta=2$ (Gaussian) is nearly optimal. This provides justification for the widespread adoption of the Gaussian mechanism in DP learning, and can be interpreted as a negative result, that optimizing over $\beta$ does not lead to meaningful improvements in performance.
An active learning framework for multi-group mean estimation
May 20, 2025Abstract:We study a fundamental learning problem over multiple groups with unknown data distributions, where an analyst would like to learn the mean of each group. Moreover, we want to ensure that this data is collected in a relatively fair manner such that the noise of the estimate of each group is reasonable. In particular, we focus on settings where data are collected dynamically, which is important in adaptive experimentation for online platforms or adaptive clinical trials for healthcare. In our model, we employ an active learning framework to sequentially collect samples with bandit feedback, observing a sample in each period from the chosen group. After observing a sample, the analyst updates their estimate of the mean and variance of that group and chooses the next group accordingly. The analyst's objective is to dynamically collect samples to minimize the collective noise of the estimators, measured by the norm of the vector of variances of the mean estimators. We propose an algorithm, Variance-UCB, that sequentially selects groups according to an upper confidence bound on the variance estimate. We provide a general theoretical framework for providing efficient bounds on learning from any underlying distribution where the variances can be estimated reasonably. This framework yields upper bounds on regret that improve significantly upon all existing bounds, as well as a collection of new results for different objectives and distributions than those previously studied.
ClusterSC: Advancing Synthetic Control with Donor Selection
Mar 27, 2025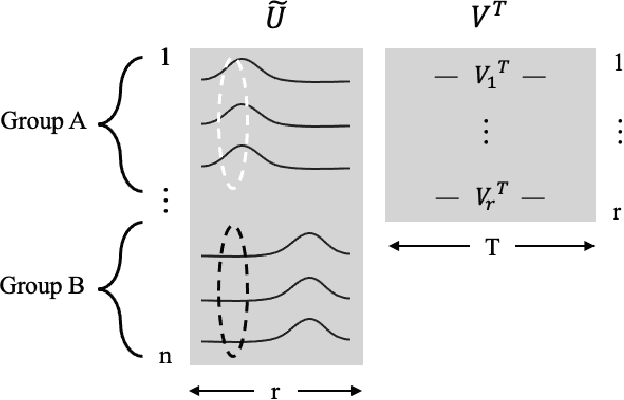
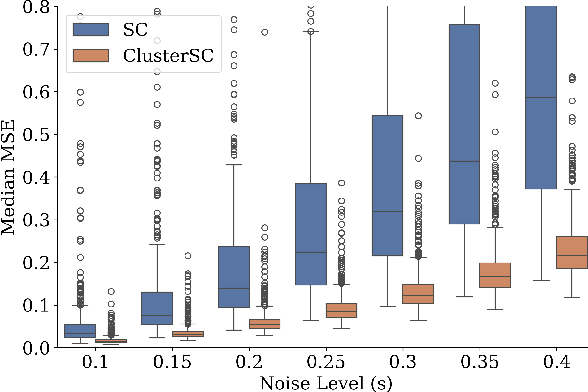
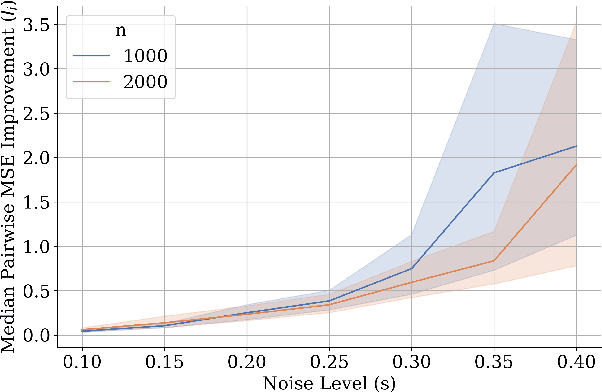
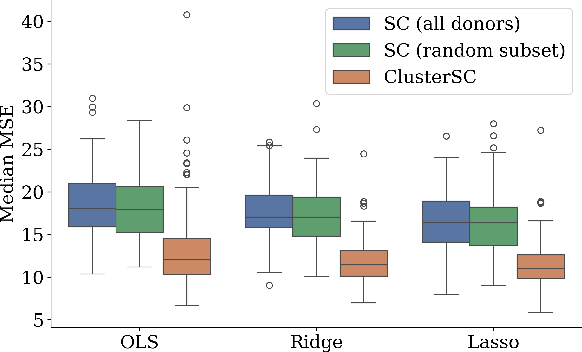
Abstract:In causal inference with observational studies, synthetic control (SC) has emerged as a prominent tool. SC has traditionally been applied to aggregate-level datasets, but more recent work has extended its use to individual-level data. As they contain a greater number of observed units, this shift introduces the curse of dimensionality to SC. To address this, we propose Cluster Synthetic Control (ClusterSC), based on the idea that groups of individuals may exist where behavior aligns internally but diverges between groups. ClusterSC incorporates a clustering step to select only the relevant donors for the target. We provide theoretical guarantees on the improvements induced by ClusterSC, supported by empirical demonstrations on synthetic and real-world datasets. The results indicate that ClusterSC consistently outperforms classical SC approaches.
Differential Privacy Under Class Imbalance: Methods and Empirical Insights
Nov 08, 2024



Abstract:Imbalanced learning occurs in classification settings where the distribution of class-labels is highly skewed in the training data, such as when predicting rare diseases or in fraud detection. This class imbalance presents a significant algorithmic challenge, which can be further exacerbated when privacy-preserving techniques such as differential privacy are applied to protect sensitive training data. Our work formalizes these challenges and provides a number of algorithmic solutions. We consider DP variants of pre-processing methods that privately augment the original dataset to reduce the class imbalance; these include oversampling, SMOTE, and private synthetic data generation. We also consider DP variants of in-processing techniques, which adjust the learning algorithm to account for the imbalance; these include model bagging, class-weighted empirical risk minimization and class-weighted deep learning. For each method, we either adapt an existing imbalanced learning technique to the private setting or demonstrate its incompatibility with differential privacy. Finally, we empirically evaluate these privacy-preserving imbalanced learning methods under various data and distributional settings. We find that private synthetic data methods perform well as a data pre-processing step, while class-weighted ERMs are an alternative in higher-dimensional settings where private synthetic data suffers from the curse of dimensionality.
Thompson Sampling Itself is Differentially Private
Jul 20, 2024



Abstract:In this work we first show that the classical Thompson sampling algorithm for multi-arm bandits is differentially private as-is, without any modification. We provide per-round privacy guarantees as a function of problem parameters and show composition over $T$ rounds; since the algorithm is unchanged, existing $O(\sqrt{NT\log N})$ regret bounds still hold and there is no loss in performance due to privacy. We then show that simple modifications -- such as pre-pulling all arms a fixed number of times, increasing the sampling variance -- can provide tighter privacy guarantees. We again provide privacy guarantees that now depend on the new parameters introduced in the modification, which allows the analyst to tune the privacy guarantee as desired. We also provide a novel regret analysis for this new algorithm, and show how the new parameters also impact expected regret. Finally, we empirically validate and illustrate our theoretical findings in two parameter regimes and demonstrate that tuning the new parameters substantially improve the privacy-regret tradeoff.
Mean Estimation with User-level Privacy under Data Heterogeneity
Jul 28, 2023Abstract:A key challenge in many modern data analysis tasks is that user data are heterogeneous. Different users may possess vastly different numbers of data points. More importantly, it cannot be assumed that all users sample from the same underlying distribution. This is true, for example in language data, where different speech styles result in data heterogeneity. In this work we propose a simple model of heterogeneous user data that allows user data to differ in both distribution and quantity of data, and provide a method for estimating the population-level mean while preserving user-level differential privacy. We demonstrate asymptotic optimality of our estimator and also prove general lower bounds on the error achievable in the setting we introduce.
Differentially Private Synthetic Control
Mar 24, 2023



Abstract:Synthetic control is a causal inference tool used to estimate the treatment effects of an intervention by creating synthetic counterfactual data. This approach combines measurements from other similar observations (i.e., donor pool ) to predict a counterfactual time series of interest (i.e., target unit) by analyzing the relationship between the target and the donor pool before the intervention. As synthetic control tools are increasingly applied to sensitive or proprietary data, formal privacy protections are often required. In this work, we provide the first algorithms for differentially private synthetic control with explicit error bounds. Our approach builds upon tools from non-private synthetic control and differentially private empirical risk minimization. We provide upper and lower bounds on the sensitivity of the synthetic control query and provide explicit error bounds on the accuracy of our private synthetic control algorithms. We show that our algorithms produce accurate predictions for the target unit, and that the cost of privacy is small. Finally, we empirically evaluate the performance of our algorithm, and show favorable performance in a variety of parameter regimes, as well as providing guidance to practitioners for hyperparameter tuning.
Robust Estimation under the Wasserstein Distance
Feb 02, 2023



Abstract:We study the problem of robust distribution estimation under the Wasserstein metric, a popular discrepancy measure between probability distributions rooted in optimal transport (OT) theory. We introduce a new outlier-robust Wasserstein distance $\mathsf{W}_p^\varepsilon$ which allows for $\varepsilon$ outlier mass to be removed from its input distributions, and show that minimum distance estimation under $\mathsf{W}_p^\varepsilon$ achieves minimax optimal robust estimation risk. Our analysis is rooted in several new results for partial OT, including an approximate triangle inequality, which may be of independent interest. To address computational tractability, we derive a dual formulation for $\mathsf{W}_p^\varepsilon$ that adds a simple penalty term to the classic Kantorovich dual objective. As such, $\mathsf{W}_p^\varepsilon$ can be implemented via an elementary modification to standard, duality-based OT solvers. Our results are extended to sliced OT, where distributions are projected onto low-dimensional subspaces, and applications to homogeneity and independence testing are explored. We illustrate the virtues of our framework via applications to generative modeling with contaminated datasets.
Private Sequential Hypothesis Testing for Statisticians: Privacy, Error Rates, and Sample Size
Apr 10, 2022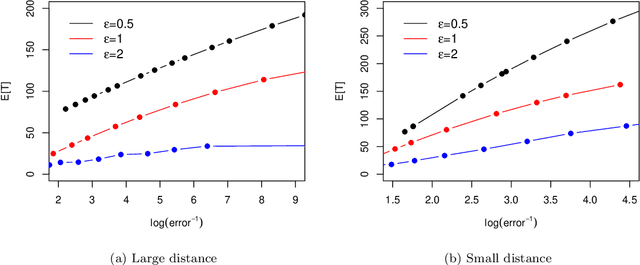
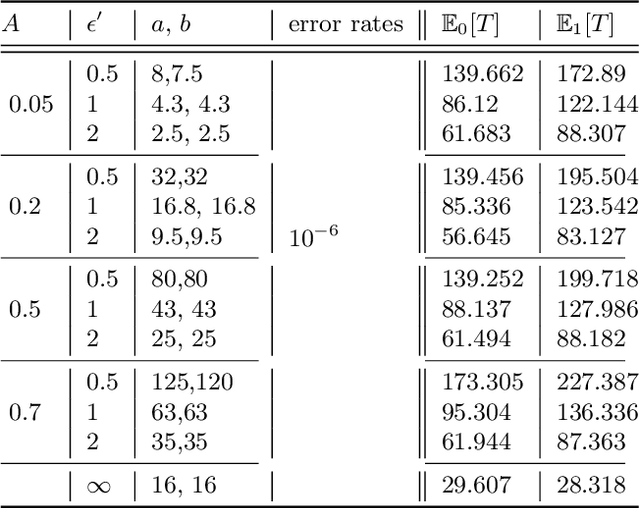
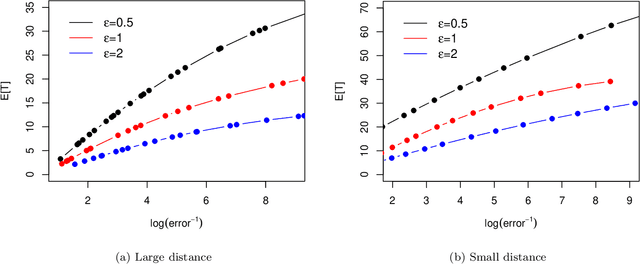
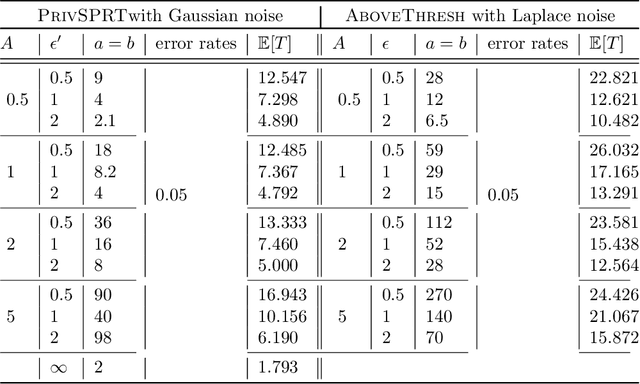
Abstract:The sequential hypothesis testing problem is a class of statistical analyses where the sample size is not fixed in advance. Instead, the decision-process takes in new observations sequentially to make real-time decisions for testing an alternative hypothesis against a null hypothesis until some stopping criterion is satisfied. In many common applications of sequential hypothesis testing, the data can be highly sensitive and may require privacy protection; for example, sequential hypothesis testing is used in clinical trials, where doctors sequentially collect data from patients and must determine when to stop recruiting patients and whether the treatment is effective. The field of differential privacy has been developed to offer data analysis tools with strong privacy guarantees, and has been commonly applied to machine learning and statistical tasks. In this work, we study the sequential hypothesis testing problem under a slight variant of differential privacy, known as Renyi differential privacy. We present a new private algorithm based on Wald's Sequential Probability Ratio Test (SPRT) that also gives strong theoretical privacy guarantees. We provide theoretical analysis on statistical performance measured by Type I and Type II error as well as the expected sample size. We also empirically validate our theoretical results on several synthetic databases, showing that our algorithms also perform well in practice. Unlike previous work in private hypothesis testing that focused only on the classical fixed sample setting, our results in the sequential setting allow a conclusion to be reached much earlier, and thus saving the cost of collecting additional samples.
Outlier-Robust Optimal Transport: Duality, Structure, and Statistical Analysis
Nov 05, 2021
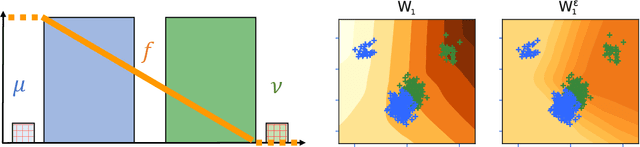

Abstract:The Wasserstein distance, rooted in optimal transport (OT) theory, is a popular discrepancy measure between probability distributions with various applications to statistics and machine learning. Despite their rich structure and demonstrated utility, Wasserstein distances are sensitive to outliers in the considered distributions, which hinders applicability in practice. Inspired by the Huber contamination model, we propose a new outlier-robust Wasserstein distance $\mathsf{W}_p^\varepsilon$ which allows for $\varepsilon$ outlier mass to be removed from each contaminated distribution. Our formulation amounts to a highly regular optimization problem that lends itself better for analysis compared to previously considered frameworks. Leveraging this, we conduct a thorough theoretical study of $\mathsf{W}_p^\varepsilon$, encompassing characterization of optimal perturbations, regularity, duality, and statistical estimation and robustness results. In particular, by decoupling the optimization variables, we arrive at a simple dual form for $\mathsf{W}_p^\varepsilon$ that can be implemented via an elementary modification to standard, duality-based OT solvers. We illustrate the benefits of our framework via applications to generative modeling with contaminated datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge