Modified Gauss-Newton Algorithms under Noise

Gauss-Newton methods and their stochastic version have been widely used in machine learning and signal processing. Their nonsmooth counterparts, modified Gauss-Newton or prox-linear algorithms, can lead to contrasting outcomes when compared to gradient descent in large-scale statistical settings. We explore the contrasting performance of these two classes of algorithms in theory on a stylized statistical example, and experimentally on learning problems including structured prediction. In theory, we delineate the regime where the quadratic convergence of the modified Gauss-Newton method is active under statistical noise. In the experiments, we underline the versatility of stochastic (sub)-gradient descent to minimize nonsmooth composite objectives.

Confidence Sets under Generalized Self-Concordance

This paper revisits a fundamental problem in statistical inference from a non-asymptotic theoretical viewpoint $\unicode{x2013}$ the construction of confidence sets. We establish a finite-sample bound for the estimator, characterizing its asymptotic behavior in a non-asymptotic fashion. An important feature of our bound is that its dimension dependency is captured by the effective dimension $\unicode{x2013}$ the trace of the limiting sandwich covariance $\unicode{x2013}$ which can be much smaller than the parameter dimension in some regimes. We then illustrate how the bound can be used to obtain a confidence set whose shape is adapted to the optimization landscape induced by the loss function. Unlike previous works that rely heavily on the strong convexity of the loss function, we only assume the Hessian is lower bounded at optimum and allow it to gradually becomes degenerate. This property is formalized by the notion of generalized self-concordance which originated from convex optimization. Moreover, we demonstrate how the effective dimension can be estimated from data and characterize its estimation accuracy. We apply our results to maximum likelihood estimation with generalized linear models, score matching with exponential families, and hypothesis testing with Rao's score test.

MAUVE Scores for Generative Models: Theory and Practice

Generative AI has matured to a point where large-scale models can generate text that seems indistinguishable from human-written text and remarkably photorealistic images. Automatically measuring how close the distribution of generated data is to the target real data distribution is a key step in diagnosing existing models and developing better models. We present MAUVE, a family of comparison measures between pairs of distributions such as those encountered in the generative modeling of text or images. These scores are statistical summaries of divergence frontiers capturing two types of errors in generative modeling. We explore four approaches to statistically estimate these scores: vector quantization, non-parametric estimation, classifier-based estimation, and parametric Gaussian approximations. We provide statistical bounds for the vector quantization approach. Empirically, we find that the proposed scores paired with a range of $f$-divergences and statistical estimation methods can quantify the gaps between the distributions of human-written text and those of modern neural language models by correlating with human judgments and identifying known properties of the generated texts. We conclude the paper by demonstrating its applications to other AI domains and discussing practical recommendations.

Stochastic Optimization for Spectral Risk Measures

Spectral risk objectives - also called $L$-risks - allow for learning systems to interpolate between optimizing average-case performance (as in empirical risk minimization) and worst-case performance on a task. We develop stochastic algorithms to optimize these quantities by characterizing their subdifferential and addressing challenges such as biasedness of subgradient estimates and non-smoothness of the objective. We show theoretically and experimentally that out-of-the-box approaches such as stochastic subgradient and dual averaging are hindered by bias and that our approach outperforms them.

Statistical and Computational Guarantees for Influence Diagnostics

Influence diagnostics such as influence functions and approximate maximum influence perturbations are popular in machine learning and in AI domain applications. Influence diagnostics are powerful statistical tools to identify influential datapoints or subsets of datapoints. We establish finite-sample statistical bounds, as well as computational complexity bounds, for influence functions and approximate maximum influence perturbations using efficient inverse-Hessian-vector product implementations. We illustrate our results with generalized linear models and large attention based models on synthetic and real data.

Stochastic optimization on matrices and a graphon McKean-Vlasov limit

We consider stochastic gradient descents on the space of large symmetric matrices of suitable functions that are invariant under permuting the rows and columns using the same permutation. We establish deterministic limits of these random curves as the dimensions of the matrices go to infinity while the entries remain bounded. Under a ``small noise'' assumption the limit is shown to be the gradient flow of functions on graphons whose existence was established in arXiv:2111.09459. We also consider limits of stochastic gradient descents with added properly scaled reflected Brownian noise. The limiting curve of graphons is characterized by a family of stochastic differential equations with reflections and can be thought of as an extension of the classical McKean-Vlasov limit for interacting diffusions. The proofs introduce a family of infinite-dimensional exchangeable arrays of reflected diffusions and a novel notion of propagation of chaos for large matrices of interacting diffusions.

Iterative Linear Quadratic Optimization for Nonlinear Control: Differentiable Programming Algorithmic Templates

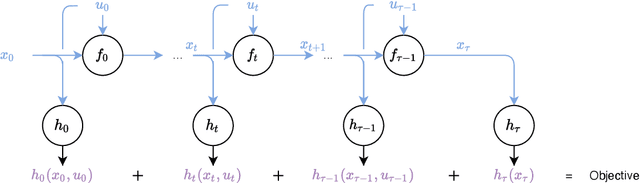
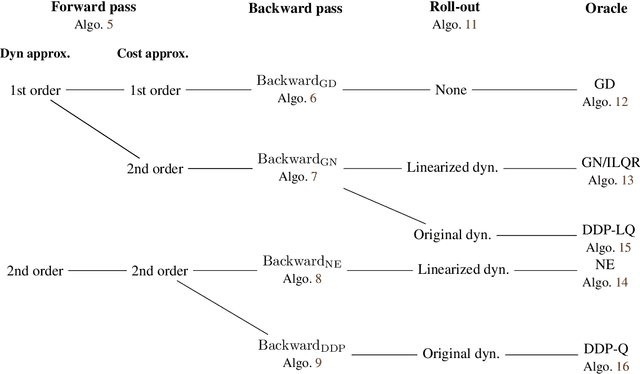
We present the implementation of nonlinear control algorithms based on linear and quadratic approximations of the objective from a functional viewpoint. We present a gradient descent, a Gauss-Newton method, a Newton method, differential dynamic programming approaches with linear quadratic or quadratic approximations, various line-search strategies, and regularized variants of these algorithms. We derive the computational complexities of all algorithms in a differentiable programming framework and present sufficient optimality conditions. We compare the algorithms on several benchmarks, such as autonomous car racing using a bicycle model of a car. The algorithms are coded in a differentiable programming language in a publicly available package.

Orthogonal Statistical Learning with Self-Concordant Loss

Orthogonal statistical learning and double machine learning have emerged as general frameworks for two-stage statistical prediction in the presence of a nuisance component. We establish non-asymptotic bounds on the excess risk of orthogonal statistical learning methods with a loss function satisfying a self-concordance property. Our bounds improve upon existing bounds by a dimension factor while lifting the assumption of strong convexity. We illustrate the results with examples from multiple treatment effect estimation and generalized partially linear modeling.

Triangular Flows for Generative Modeling: Statistical Consistency, Smoothness Classes, and Fast Rates

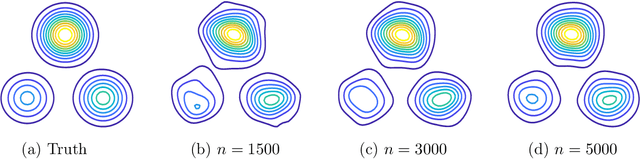
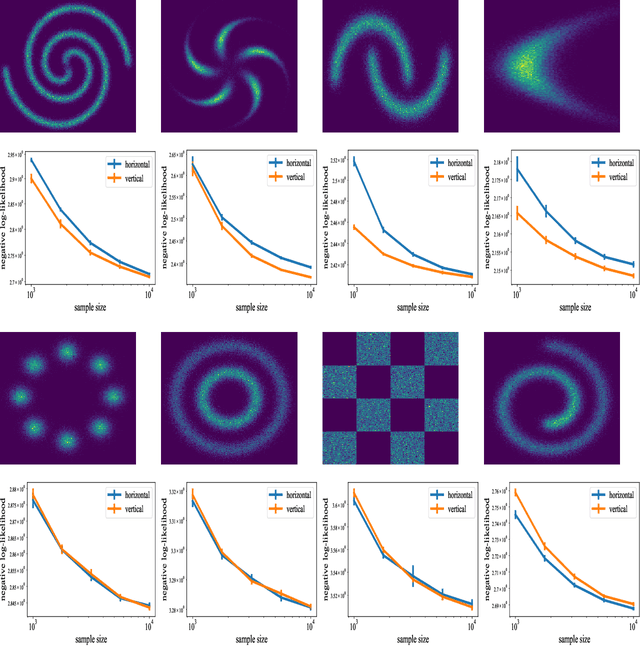
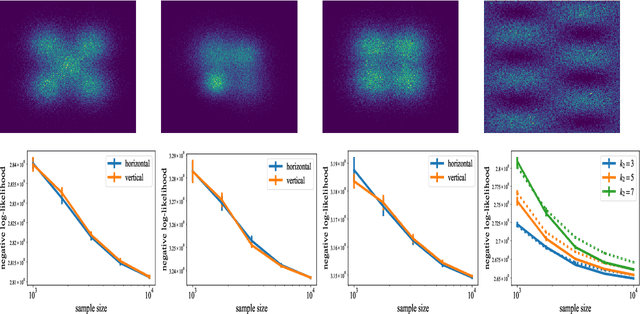
Triangular flows, also known as Kn\"{o}the-Rosenblatt measure couplings, comprise an important building block of normalizing flow models for generative modeling and density estimation, including popular autoregressive flow models such as real-valued non-volume preserving transformation models (Real NVP). We present statistical guarantees and sample complexity bounds for triangular flow statistical models. In particular, we establish the statistical consistency and the finite sample convergence rates of the Kullback-Leibler estimator of the Kn\"{o}the-Rosenblatt measure coupling using tools from empirical process theory. Our results highlight the anisotropic geometry of function classes at play in triangular flows, shed light on optimal coordinate ordering, and lead to statistical guarantees for Jacobian flows. We conduct numerical experiments on synthetic data to illustrate the practical implications of our theoretical findings.

Entropy Regularized Optimal Transport Independence Criterion

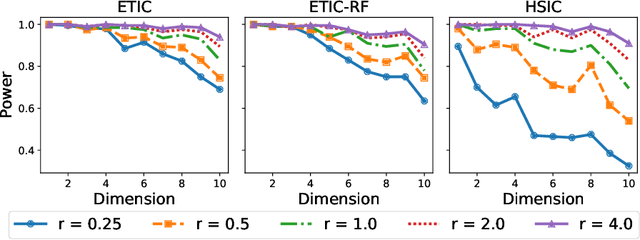
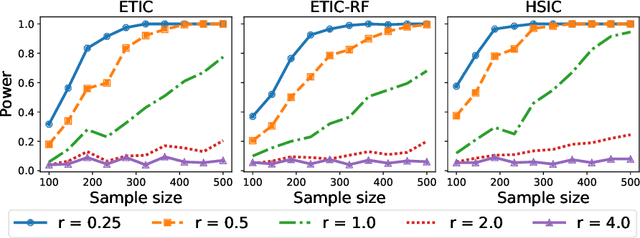
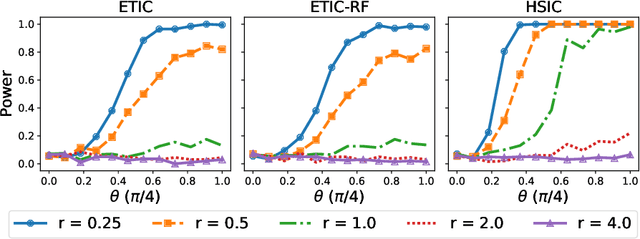
Optimal transport (OT) and its entropy regularized offspring have recently gained a lot of attention in both machine learning and AI domains. In particular, optimal transport has been used to develop probability metrics between probability distributions. We introduce in this paper an independence criterion based on entropy regularized optimal transport. Our criterion can be used to test for independence between two samples. We establish non-asymptotic bounds for our test statistic, and study its statistical behavior under both the null and alternative hypothesis. Our theoretical results involve tools from U-process theory and optimal transport theory. We present experimental results on existing benchmarks, illustrating the interest of the proposed criterion.