Just Least Squares: Binary Compressive Sampling with Low Generative Intrinsic Dimension

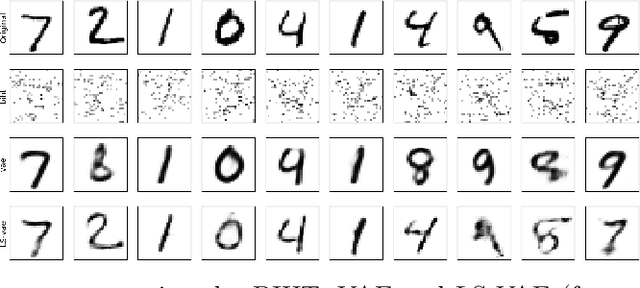
In this paper, we consider recovering $n$ dimensional signals from $m$ binary measurements corrupted by noises and sign flips under the assumption that the target signals have low generative intrinsic dimension, i.e., the target signals can be approximately generated via an $L$-Lipschitz generator $G: \mathbb{R}^k\rightarrow\mathbb{R}^{n}, k\ll n$. Although the binary measurements model is highly nonlinear, we propose a least square decoder and prove that, up to a constant $c$, with high probability, the least square decoder achieves a sharp estimation error $\mathcal{O} (\sqrt{\frac{k\log (Ln)}{m}})$ as long as $m\geq \mathcal{O}( k\log (Ln))$. Extensive numerical simulations and comparisons with state-of-the-art methods demonstrated the least square decoder is robust to noise and sign flips, as indicated by our theory. By constructing a ReLU network with properly chosen depth and width, we verify the (approximately) deep generative prior, which is of independent interest.

A Data-Driven Line Search Rule for Support Recovery in High-dimensional Data Analysis

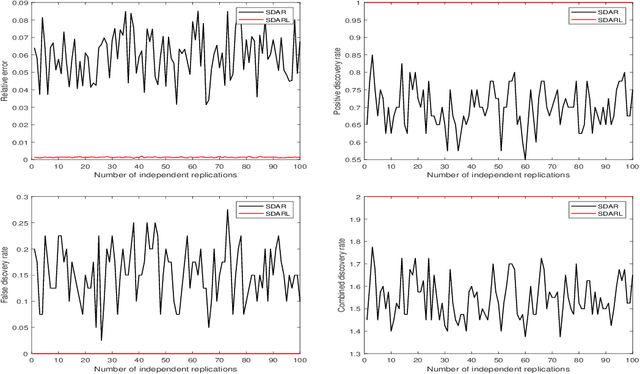
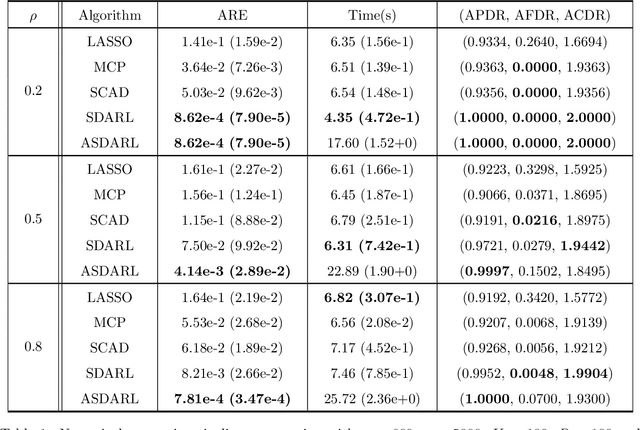
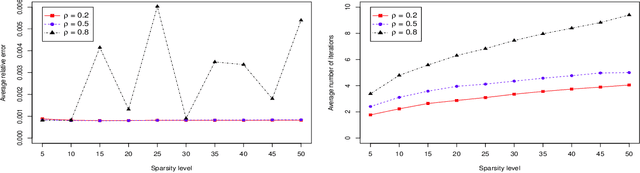
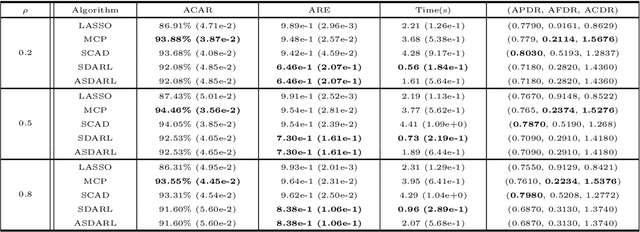
In this work, we consider the algorithm to the (nonlinear) regression problems with $\ell_0$ penalty. The existing algorithms for $\ell_0$ based optimization problem are often carried out with a fixed step size, and the selection of an appropriate step size depends on the restricted strong convexity and smoothness for the loss function, hence it is difficult to compute in practical calculation. In sprite of the ideas of support detection and root finding \cite{HJK2020}, we proposes a novel and efficient data-driven line search rule to adaptively determine the appropriate step size. We prove the $\ell_2$ error bound to the proposed algorithm without much restrictions for the cost functional. A large number of numerical comparisons with state-of-the-art algorithms in linear and logistic regression problems show the stability, effectiveness and superiority of the proposed algorithms.

Non-Asymptotic Error Bounds for Bidirectional GANs

We derive nearly sharp bounds for the bidirectional GAN (BiGAN) estimation error under the Dudley distance between the latent joint distribution and the data joint distribution with appropriately specified architecture of the neural networks used in the model. To the best of our knowledge, this is the first theoretical guarantee for the bidirectional GAN learning approach. An appealing feature of our results is that they do not assume the reference and the data distributions to have the same dimensions or these distributions to have bounded support. These assumptions are commonly assumed in the existing convergence analysis of the unidirectional GANs but may not be satisfied in practice. Our results are also applicable to the Wasserstein bidirectional GAN if the target distribution is assumed to have a bounded support. To prove these results, we construct neural network functions that push forward an empirical distribution to another arbitrary empirical distribution on a possibly different-dimensional space. We also develop a novel decomposition of the integral probability metric for the error analysis of bidirectional GANs. These basic theoretical results are of independent interest and can be applied to other related learning problems.

Relative Entropy Gradient Sampler for Unnormalized Distributions

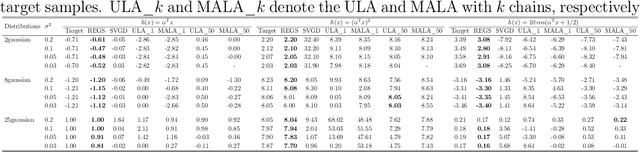
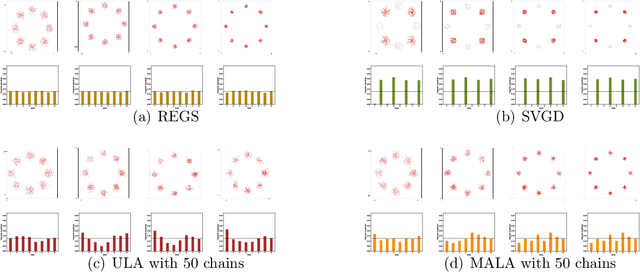
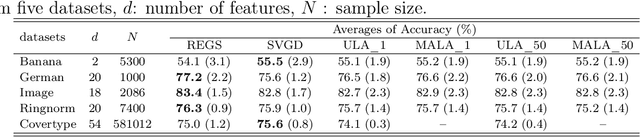
We propose a relative entropy gradient sampler (REGS) for sampling from unnormalized distributions. REGS is a particle method that seeks a sequence of simple nonlinear transforms iteratively pushing the initial samples from a reference distribution into the samples from an unnormalized target distribution. To determine the nonlinear transforms at each iteration, we consider the Wasserstein gradient flow of relative entropy. This gradient flow determines a path of probability distributions that interpolates the reference distribution and the target distribution. It is characterized by an ODE system with velocity fields depending on the density ratios of the density of evolving particles and the unnormalized target density. To sample with REGS, we need to estimate the density ratios and simulate the ODE system with particle evolution. We propose a novel nonparametric approach to estimating the logarithmic density ratio using neural networks. Extensive simulation studies on challenging multimodal 1D and 2D mixture distributions and Bayesian logistic regression on real datasets demonstrate that the REGS outperforms the state-of-the-art sampling methods included in the comparison.

Coordinate Descent for MCP/SCAD Penalized Least Squares Converges Linearly

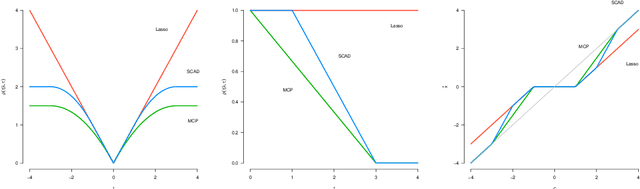
Recovering sparse signals from observed data is an important topic in signal/imaging processing, statistics and machine learning. Nonconvex penalized least squares have been attracted a lot of attentions since they enjoy nice statistical properties. Computationally, coordinate descent (CD) is a workhorse for minimizing the nonconvex penalized least squares criterion due to its simplicity and scalability. In this work, we prove the linear convergence rate to CD for solving MCP/SCAD penalized least squares problems.

Convergence Analysis of Schr{ö}dinger-F{ö}llmer Sampler without Convexity

Schr\"{o}dinger-F\"{o}llmer sampler (SFS) is a novel and efficient approach for sampling from possibly unnormalized distributions without ergodicity. SFS is based on the Euler-Maruyama discretization of Schr\"{o}dinger-F\"{o}llmer diffusion process $$\mathrm{d} X_{t}=-\nabla U\left(X_t, t\right) \mathrm{d} t+\mathrm{d} B_{t}, \quad t \in[0,1],\quad X_0=0$$ on the unit interval, which transports the degenerate distribution at time zero to the target distribution at time one. In \cite{sfs21}, the consistency of SFS is established under a restricted assumption that %the drift term $b(x,t)$ the potential $U(x,t)$ is uniformly (on $t$) strongly %concave convex (on $x$). In this paper we provide a nonasymptotic error bound of SFS in Wasserstein distance under some smooth and bounded conditions on the density ratio of the target distribution over the standard normal distribution, but without requiring the strongly convexity of the potential.

Deep Generative Learning via Schrödinger Bridge

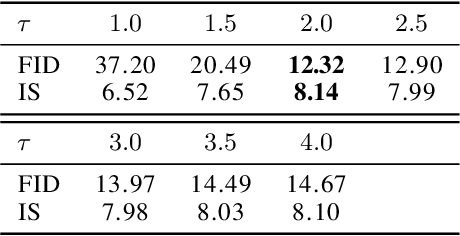
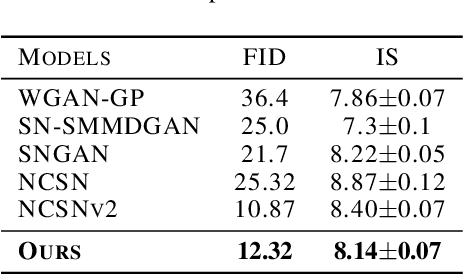
We propose to learn a generative model via entropy interpolation with a Schr\"{o}dinger Bridge. The generative learning task can be formulated as interpolating between a reference distribution and a target distribution based on the Kullback-Leibler divergence. At the population level, this entropy interpolation is characterized via an SDE on $[0,1]$ with a time-varying drift term. At the sample level, we derive our Schr\"{o}dinger Bridge algorithm by plugging the drift term estimated by a deep score estimator and a deep density ratio estimator into the Euler-Maruyama method. Under some mild smoothness assumptions of the target distribution, we prove the consistency of both the score estimator and the density ratio estimator, and then establish the consistency of the proposed Schr\"{o}dinger Bridge approach. Our theoretical results guarantee that the distribution learned by our approach converges to the target distribution. Experimental results on multimodal synthetic data and benchmark data support our theoretical findings and indicate that the generative model via Schr\"{o}dinger Bridge is comparable with state-of-the-art GANs, suggesting a new formulation of generative learning. We demonstrate its usefulness in image interpolation and image inpainting.

An error analysis of generative adversarial networks for learning distributions

This paper studies how well generative adversarial networks (GANs) learn probability distributions from finite samples. Our main results establish the convergence rates of GANs under a collection of integral probability metrics defined through H\"older classes, including the Wasserstein distance as a special case. We also show that GANs are able to adaptively learn data distributions with low-dimensional structures or have H\"older densities, when the network architectures are chosen properly. In particular, for distributions concentrated around a low-dimensional set, we show that the learning rates of GANs do not depend on the high ambient dimension, but on the lower intrinsic dimension. Our analysis is based on a new oracle inequality decomposing the estimation error into the generator and discriminator approximation error and the statistical error, which may be of independent interest.

Non-asymptotic Excess Risk Bounds for Classification with Deep Convolutional Neural Networks

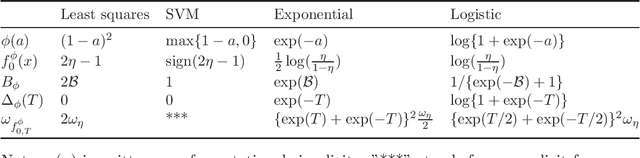
In this paper, we consider the problem of binary classification with a class of general deep convolutional neural networks, which includes fully-connected neural networks and fully convolutional neural networks as special cases. We establish non-asymptotic excess risk bounds for a class of convex surrogate losses and target functions with different modulus of continuity. An important feature of our results is that we clearly define the prefactors of the risk bounds in terms of the input data dimension and other model parameters and show that they depend polynomially on the dimensionality in some important models. We also show that the classification methods with CNNs can circumvent the curse of dimensionality if the input data is supported on an approximate low-dimensional manifold. To establish these results, we derive an upper bound for the covering number for the class of general convolutional neural networks with a bias term in each convolutional layer, and derive new results on the approximation power of CNNs for any uniformly-continuous target functions. These results provide further insights into the complexity and the approximation power of general convolutional neural networks, which are of independent interest and may have other applications. Finally, we apply our general results to analyze the non-asymptotic excess risk bounds for four widely used methods with different loss functions using CNNs, including the least squares, the logistic, the exponential and the SVM hinge losses.

Deep Neural Networks with ReLU-Sine-Exponential Activations Break Curse of Dimensionality on Hölder Class

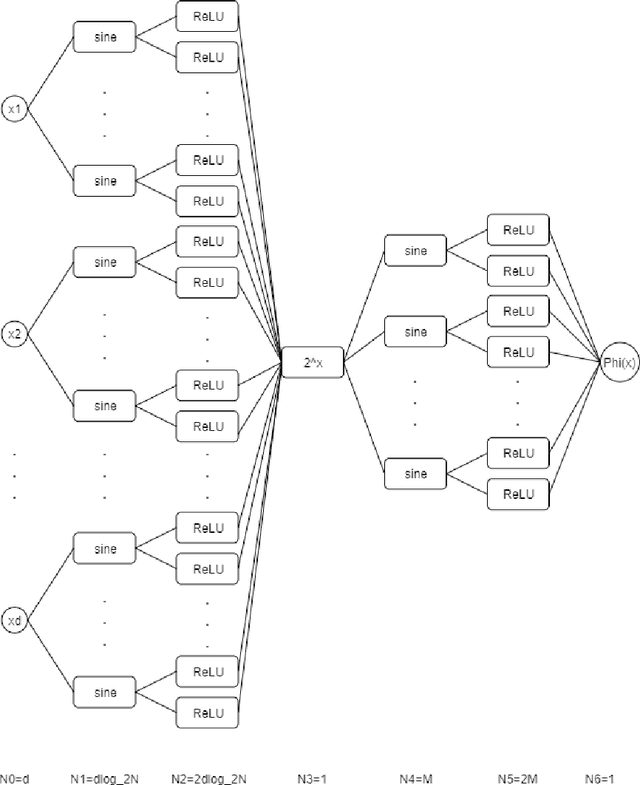
In this paper, we construct neural networks with ReLU, sine and $2^x$ as activation functions. For general continuous $f$ defined on $[0,1]^d$ with continuity modulus $\omega_f(\cdot)$, we construct ReLU-sine-$2^x$ networks that enjoy an approximation rate $\mathcal{O}(\omega_f(\sqrt{d})\cdot2^{-M}+\omega_{f}\left(\frac{\sqrt{d}}{N}\right))$, where $M,N\in \mathbb{N}^{+}$ denote the hyperparameters related to widths of the networks. As a consequence, we can construct ReLU-sine-$2^x$ network with the depth $5$ and width $\max\left\{\left\lceil2d^{3/2}\left(\frac{3\mu}{\epsilon}\right)^{1/{\alpha}}\right\rceil,2\left\lceil\log_2\frac{3\mu d^{\alpha/2}}{2\epsilon}\right\rceil+2\right\}$ that approximates $f\in \mathcal{H}_{\mu}^{\alpha}([0,1]^d)$ within a given tolerance $\epsilon >0$ measured in $L^p$ norm $p\in[1,\infty)$, where $\mathcal{H}_{\mu}^{\alpha}([0,1]^d)$ denotes the H\"older continuous function class defined on $[0,1]^d$ with order $\alpha \in (0,1]$ and constant $\mu > 0$. Therefore, the ReLU-sine-$2^x$ networks overcome the curse of dimensionality on $\mathcal{H}_{\mu}^{\alpha}([0,1]^d)$. In addition to its supper expressive power, functions implemented by ReLU-sine-$2^x$ networks are (generalized) differentiable, enabling us to apply SGD to train.