Bayesian differential programming for robust systems identification under uncertainty

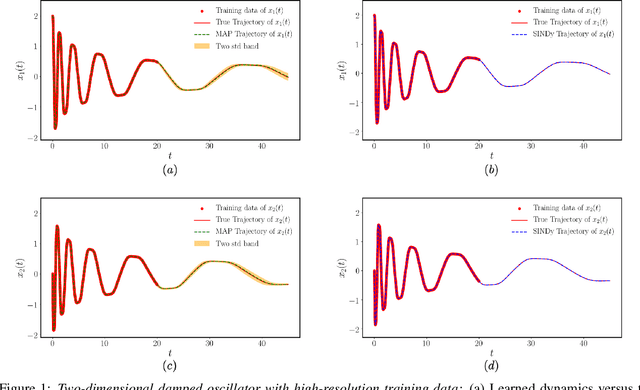
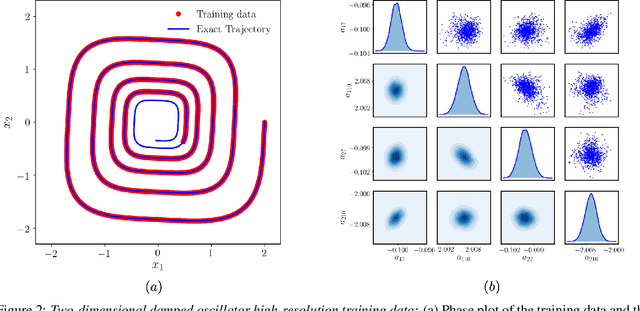
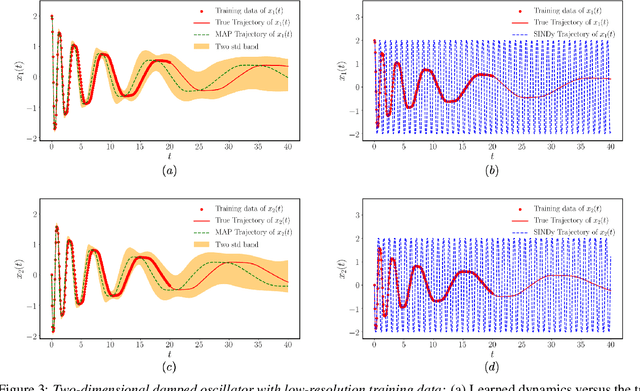
This paper presents a machine learning framework for Bayesian systems identification from noisy, sparse and irregular observations of nonlinear dynamical systems. The proposed method takes advantage of recent developments in differentiable programming to propagate gradient information through ordinary differential equation solvers and perform Bayesian inference with respect to unknown model parameters using Hamiltonian Monte Carlo. This allows us to efficiently infer posterior distributions over plausible models with quantified uncertainty, while the use of sparsity-promoting priors enables the discovery of interpretable and parsimonious representations for the underlying latent dynamics. A series of numerical studies is presented to demonstrate the effectiveness of the proposed methods including nonlinear oscillators, predator-prey systems, chaotic dynamics and systems biology. Taken all together, our findings put forth a novel, flexible and robust workflow for data-driven model discovery under uncertainty.

Spatial Pyramid Based Graph Reasoning for Semantic Segmentation

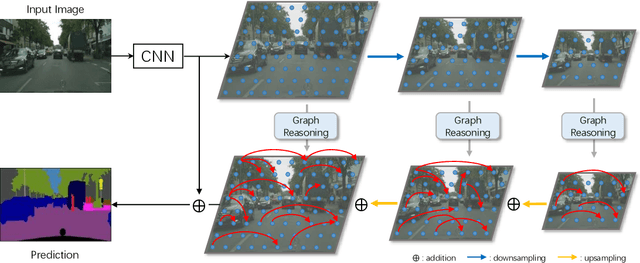
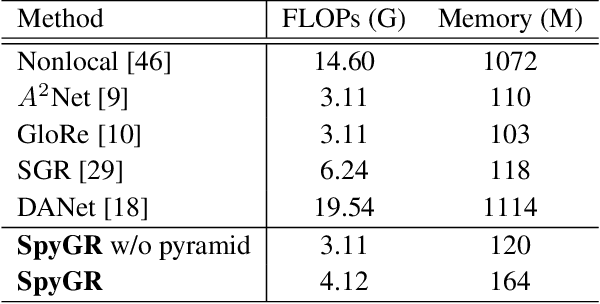
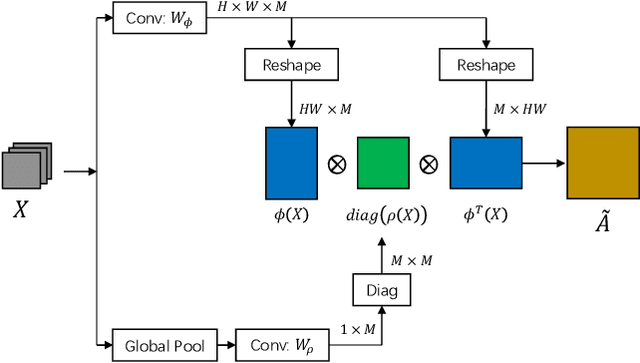
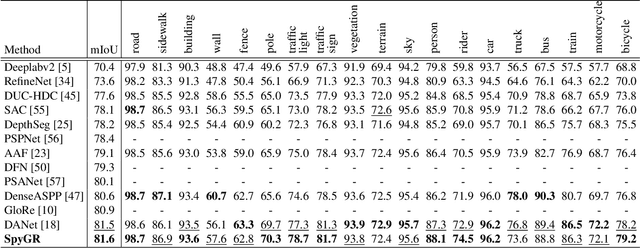
The convolution operation suffers from a limited receptive filed, while global modeling is fundamental to dense prediction tasks, such as semantic segmentation. In this paper, we apply graph convolution into the semantic segmentation task and propose an improved Laplacian. The graph reasoning is directly performed in the original feature space organized as a spatial pyramid. Different from existing methods, our Laplacian is data-dependent and we introduce an attention diagonal matrix to learn a better distance metric. It gets rid of projecting and re-projecting processes, which makes our proposed method a light-weight module that can be easily plugged into current computer vision architectures. More importantly, performing graph reasoning directly in the feature space retains spatial relationships and makes spatial pyramid possible to explore multiple long-range contextual patterns from different scales. Experiments on Cityscapes, COCO Stuff, PASCAL Context and PASCAL VOC demonstrate the effectiveness of our proposed methods on semantic segmentation. We achieve comparable performance with advantages in computational and memory overhead.

Variable-Bitrate Neural Compression via Bayesian Arithmetic Coding

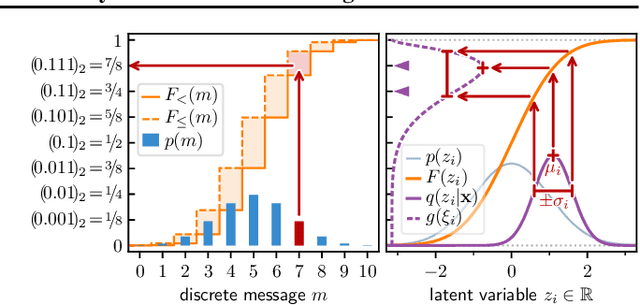
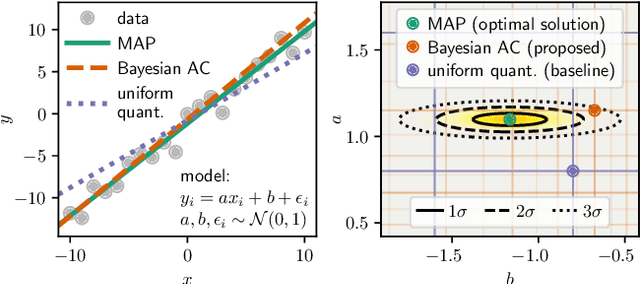
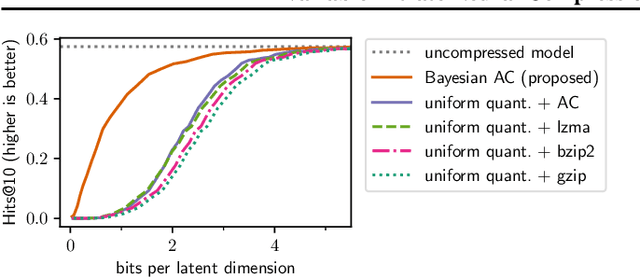
Deep Bayesian latent variable models have enabled new approaches to both model and data compression. Here, we propose a new algorithm for compressing latent representations in deep probabilistic models, such as variational autoencoders, in post-processing. The approach thus separates model design and training from the compression task. Our algorithm generalizes arithmetic coding to the continuous domain, using adaptive discretization accuracy that exploits estimates of posterior uncertainty. A consequence of the "plug and play" nature of our approach is that various rate-distortion trade-offs can be achieved with a single trained model, eliminating the need to train multiple models for different bit rates. Our experimental results demonstrate the importance of taking into account posterior uncertainties, and show that image compression with the proposed algorithm outperforms JPEG over a wide range of bit rates using only a single machine learning model. Further experiments on Bayesian neural word embeddings demonstrate the versatility of the proposed method.

Lifted Hybrid Variational Inference

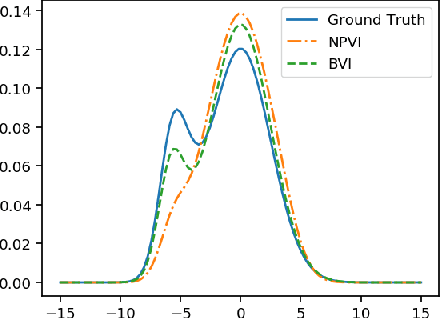
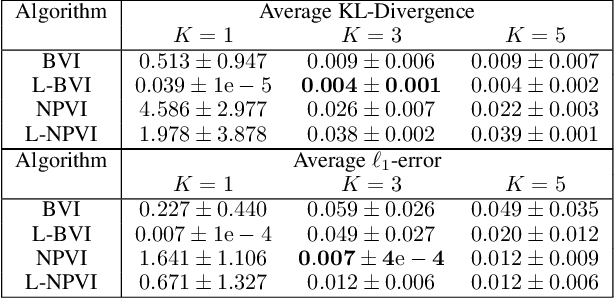
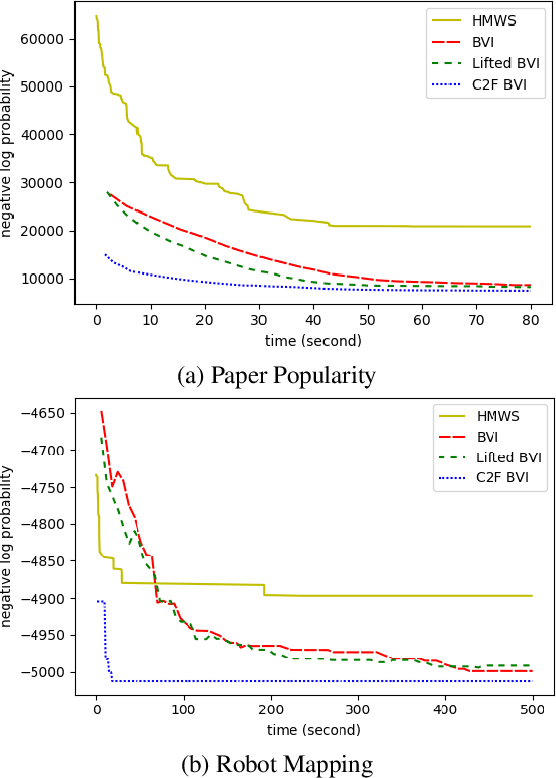
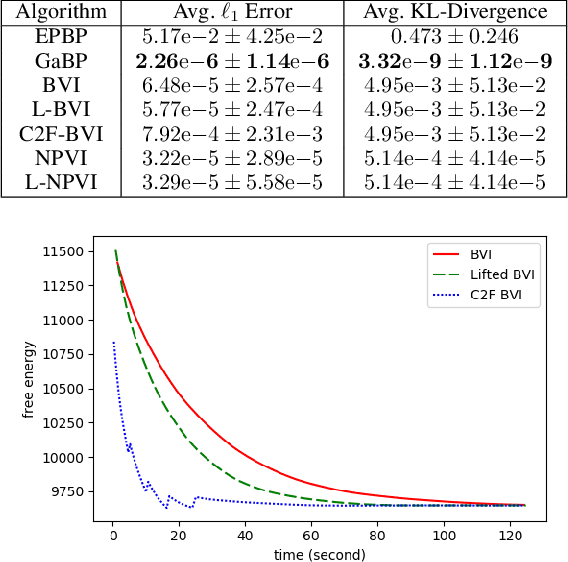
A variety of lifted inference algorithms, which exploit model symmetry to reduce computational cost, have been proposed to render inference tractable in probabilistic relational models. Most existing lifted inference algorithms operate only over discrete domains or continuous domains with restricted potential functions, e.g., Gaussian. We investigate two approximate lifted variational approaches that are applicable to hybrid domains and expressive enough to capture multi-modality. We demonstrate that the proposed variational methods are both scalable and can take advantage of approximate model symmetries, even in the presence of a large amount of continuous evidence. We demonstrate that our approach compares favorably against existing message-passing based approaches in a variety of settings. Finally, we present a sufficient condition for the Bethe approximation to yield a non-trivial estimate over the marginal polytope.

Dynamical System Inspired Adaptive Time Stepping Controller for Residual Network Families

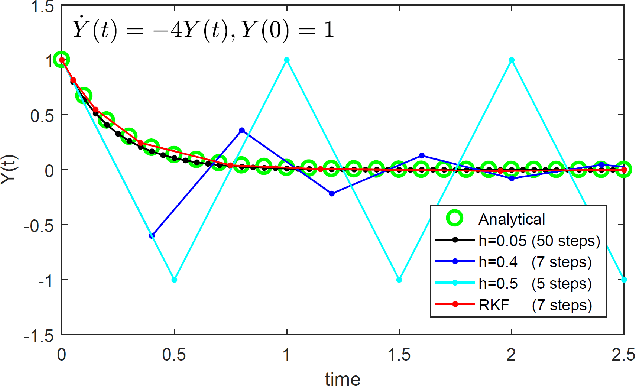
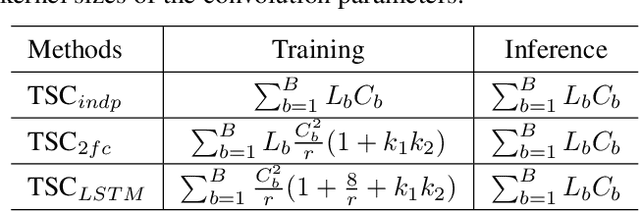
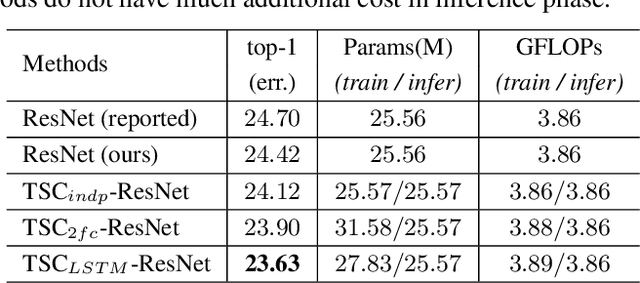
The correspondence between residual networks and dynamical systems motivates researchers to unravel the physics of ResNets with well-developed tools in numeral methods of ODE systems. The Runge-Kutta-Fehlberg method is an adaptive time stepping that renders a good trade-off between the stability and efficiency. Can we also have an adaptive time stepping for ResNets to ensure both stability and performance? In this study, we analyze the effects of time stepping on the Euler method and ResNets. We establish a stability condition for ResNets with step sizes and weight parameters, and point out the effects of step sizes on the stability and performance. Inspired by our analyses, we develop an adaptive time stepping controller that is dependent on the parameters of the current step, and aware of previous steps. The controller is jointly optimized with the network training so that variable step sizes and evolution time can be adaptively adjusted. We conduct experiments on ImageNet and CIFAR to demonstrate the effectiveness. It is shown that our proposed method is able to improve both stability and accuracy without introducing additional overhead in inference phase.

SOGNet: Scene Overlap Graph Network for Panoptic Segmentation

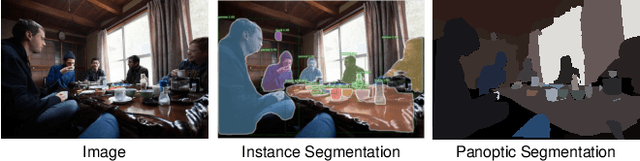
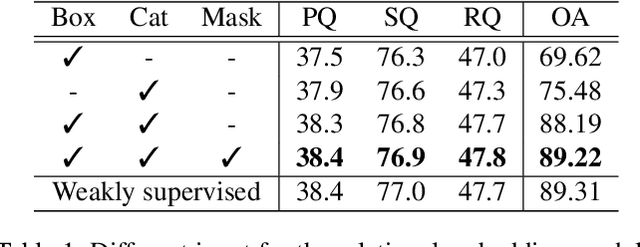
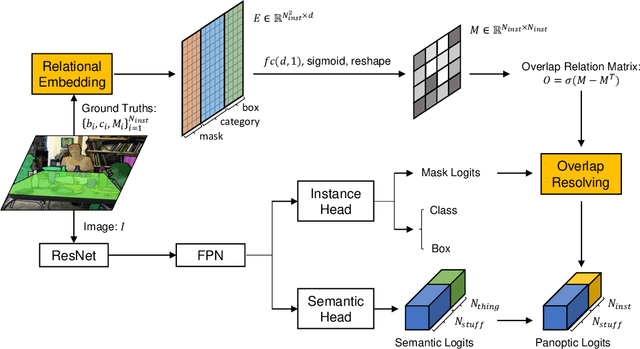
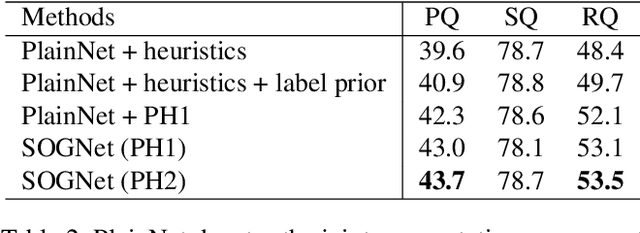
The panoptic segmentation task requires a unified result from semantic and instance segmentation outputs that may contain overlaps. However, current studies widely ignore modeling overlaps. In this study, we aim to model overlap relations among instances and resolve them for panoptic segmentation. Inspired by scene graph representation, we formulate the overlapping problem as a simplified case, named scene overlap graph. We leverage each object's category, geometry and appearance features to perform relational embedding, and output a relation matrix that encodes overlap relations. In order to overcome the lack of supervision, we introduce a differentiable module to resolve the overlap between any pair of instances. The mask logits after removing overlaps are fed into per-pixel instance \verb|id| classification, which leverages the panoptic supervision to assist in the modeling of overlap relations. Besides, we generate an approximate ground truth of overlap relations as the weak supervision, to quantify the accuracy of overlap relations predicted by our method. Experiments on COCO and Cityscapes demonstrate that our method is able to accurately predict overlap relations, and outperform the state-of-the-art performance for panoptic segmentation. Our method also won the Innovation Award in COCO 2019 challenge.

Expectation-Maximization Attention Networks for Semantic Segmentation

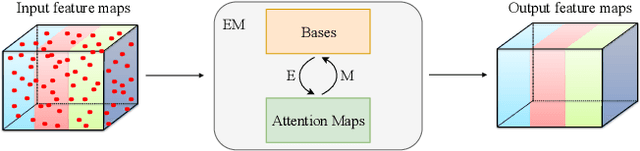
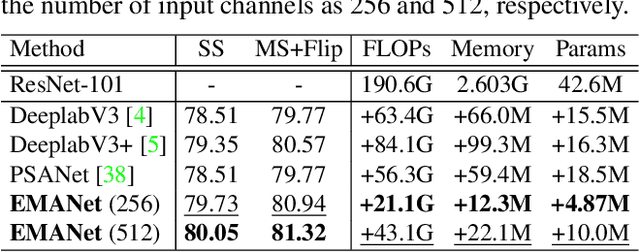
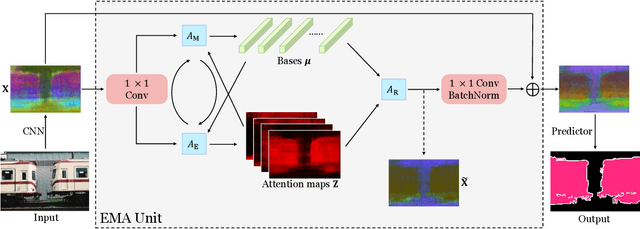
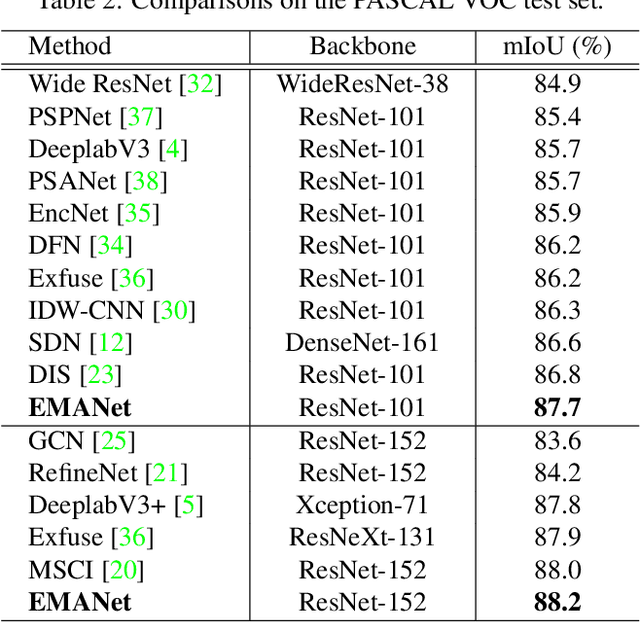
Self-attention mechanism has been widely used for various tasks. It is designed to compute the representation of each position by a weighted sum of the features at all positions. Thus, it can capture long-range relations for computer vision tasks. However, it is computationally consuming. Since the attention maps are computed w.r.t all other positions. In this paper, we formulate the attention mechanism into an expectation-maximization manner and iteratively estimate a much more compact set of bases upon which the attention maps are computed. By a weighted summation upon these bases, the resulting representation is low-rank and deprecates noisy information from the input. The proposed Expectation-Maximization Attention (EMA) module is robust to the variance of input and is also friendly in memory and computation. Moreover, we set up the bases maintenance and normalization methods to stabilize its training procedure. We conduct extensive experiments on popular semantic segmentation benchmarks including PASCAL VOC, PASCAL Context and COCO Stuff, on which we set new records.

Machine learning in cardiovascular flows modeling: Predicting pulse wave propagation from non-invasive clinical measurements using physics-informed deep learning

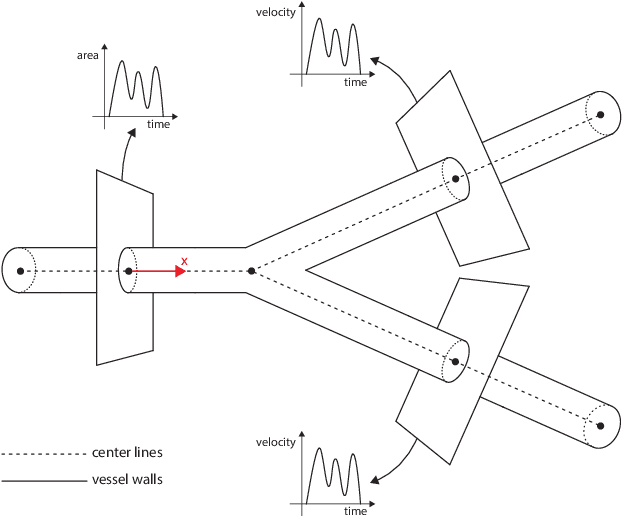
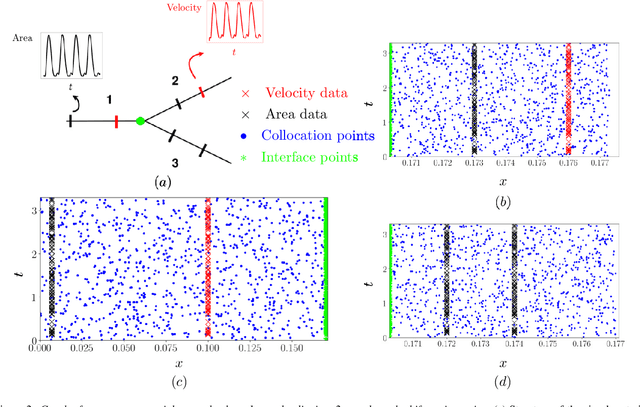
Advances in computational science offer a principled pipeline for predictive modeling of cardiovascular flows and aspire to provide a valuable tool for monitoring, diagnostics and surgical planning. Such models can be nowadays deployed on large patient-specific topologies of systemic arterial networks and return detailed predictions on flow patterns, wall shear stresses, and pulse wave propagation. However, their success heavily relies on tedious pre-processing and calibration procedures that typically induce a significant computational cost, thus hampering their clinical applicability. In this work we put forth a machine learning framework that enables the seamless synthesis of non-invasive in-vivo measurement techniques and computational flow dynamics models derived from first physical principles. We illustrate this new paradigm by showing how one-dimensional models of pulsatile flow can be used to constrain the output of deep neural networks such that their predictions satisfy the conservation of mass and momentum principles. Once trained on noisy and scattered clinical data of flow and wall displacement, these networks can return physically consistent predictions for velocity, pressure and wall displacement pulse wave propagation, all without the need to employ conventional simulators. A simple post-processing of these outputs can also provide a cheap and effective way for estimating Windkessel model parameters that are required for the calibration of traditional computational models. The effectiveness of the proposed techniques is demonstrated through a series of prototype benchmarks, as well as a realistic clinical case involving in-vivo measurements near the aorta/carotid bifurcation of a healthy human subject.

Conditional deep surrogate models for stochastic, high-dimensional, and multi-fidelity systems

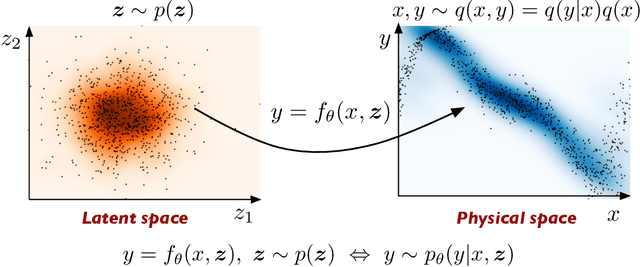
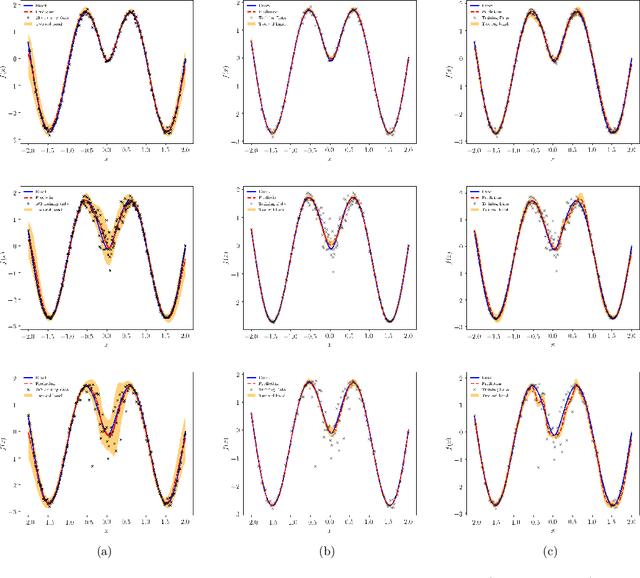
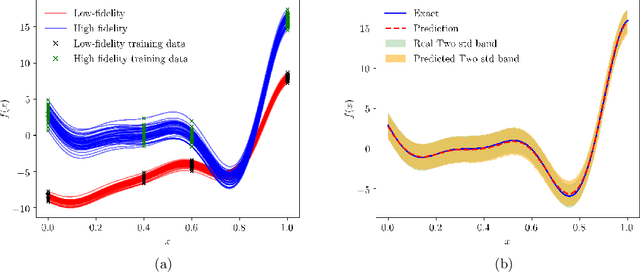
We present a probabilistic deep learning methodology that enables the construction of predictive data-driven surrogates for stochastic systems. Leveraging recent advances in variational inference with implicit distributions, we put forth a statistical inference framework that enables the end-to-end training of surrogate models on paired input-output observations that may be stochastic in nature, originate from different information sources of variable fidelity, or be corrupted by complex noise processes. The resulting surrogates can accommodate high-dimensional inputs and outputs and are able to return predictions with quantified uncertainty. The effectiveness our approach is demonstrated through a series of canonical studies, including the regression of noisy data, multi-fidelity modeling of stochastic processes, and uncertainty propagation in high-dimensional dynamical systems.

Physics-informed deep generative models

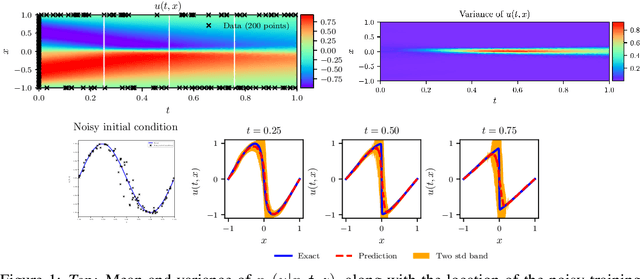
We consider the application of deep generative models in propagating uncertainty through complex physical systems. Specifically, we put forth an implicit variational inference formulation that constrains the generative model output to satisfy given physical laws expressed by partial differential equations. Such physics-informed constraints provide a regularization mechanism for effectively training deep probabilistic models for modeling physical systems in which the cost of data acquisition is high and training data-sets are typically small. This provides a scalable framework for characterizing uncertainty in the outputs of physical systems due to randomness in their inputs or noise in their observations. We demonstrate the effectiveness of our approach through a canonical example in transport dynamics.