TURF: A Two-factor, Universal, Robust, Fast Distribution Learning Algorithm

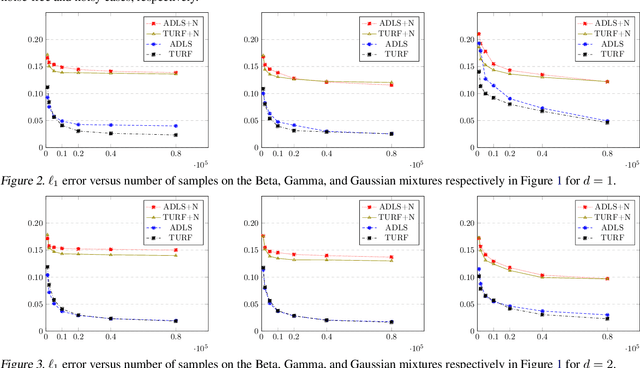
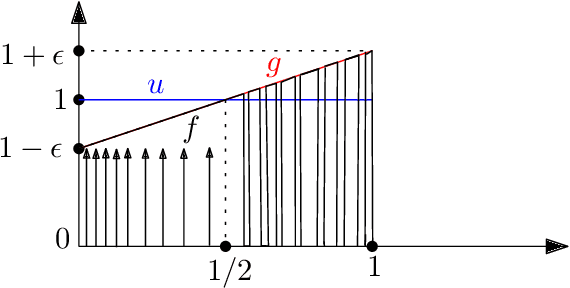
Approximating distributions from their samples is a canonical statistical-learning problem. One of its most powerful and successful modalities approximates every distribution to an $\ell_1$ distance essentially at most a constant times larger than its closest $t$-piece degree-$d$ polynomial, where $t\ge1$ and $d\ge0$. Letting $c_{t,d}$ denote the smallest such factor, clearly $c_{1,0}=1$, and it can be shown that $c_{t,d}\ge 2$ for all other $t$ and $d$. Yet current computationally efficient algorithms show only $c_{t,1}\le 2.25$ and the bound rises quickly to $c_{t,d}\le 3$ for $d\ge 9$. We derive a near-linear-time and essentially sample-optimal estimator that establishes $c_{t,d}=2$ for all $(t,d)\ne(1,0)$. Additionally, for many practical distributions, the lowest approximation distance is achieved by polynomials with vastly varying number of pieces. We provide a method that estimates this number near-optimally, hence helps approach the best possible approximation. Experiments combining the two techniques confirm improved performance over existing methodologies.

Unsupervised Embedding of Hierarchical Structure in Euclidean Space

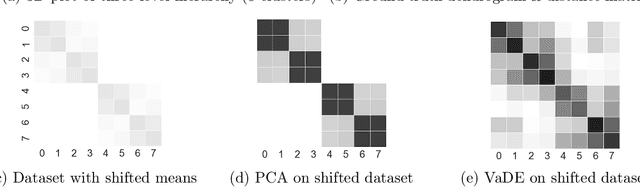
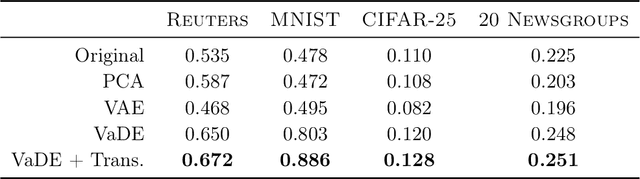
Deep embedding methods have influenced many areas of unsupervised learning. However, the best methods for learning hierarchical structure use non-Euclidean representations, whereas Euclidean geometry underlies the theory behind many hierarchical clustering algorithms. To bridge the gap between these two areas, we consider learning a non-linear embedding of data into Euclidean space as a way to improve the hierarchical clustering produced by agglomerative algorithms. To learn the embedding, we revisit using a variational autoencoder with a Gaussian mixture prior, and we show that rescaling the latent space embedding and then applying Ward's linkage-based algorithm leads to improved results for both dendrogram purity and the Moseley-Wang cost function. Finally, we complement our empirical results with a theoretical explanation of the success of this approach. We study a synthetic model of the embedded vectors and prove that Ward's method exactly recovers the planted hierarchical clustering with high probability.

Profile Entropy: A Fundamental Measure for the Learnability and Compressibility of Discrete Distributions

The profile of a sample is the multiset of its symbol frequencies. We show that for samples of discrete distributions, profile entropy is a fundamental measure unifying the concepts of estimation, inference, and compression. Specifically, profile entropy a) determines the speed of estimating the distribution relative to the best natural estimator; b) characterizes the rate of inferring all symmetric properties compared with the best estimator over any label-invariant distribution collection; c) serves as the limit of profile compression, for which we derive optimal near-linear-time block and sequential algorithms. To further our understanding of profile entropy, we investigate its attributes, provide algorithms for approximating its value, and determine its magnitude for numerous structural distribution families.

SURF: A Simple, Universal, Robust, Fast Distribution Learning Algorithm

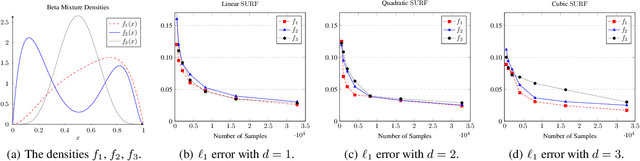
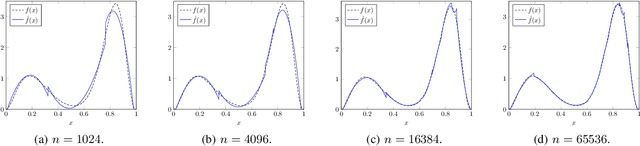
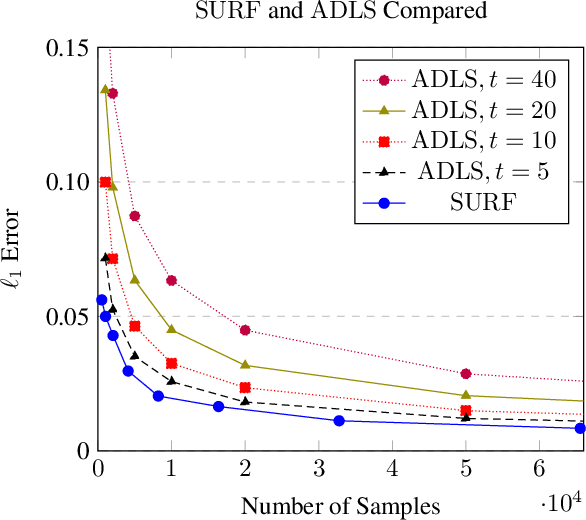
Sample- and computationally-efficient distribution estimation is a fundamental tenet in statistics and machine learning. We present $\mathrm{SURF}$, an algorithm for approximating distributions by piecewise polynomials. $\mathrm{SURF}$ is simple, replacing existing general-purpose optimization techniques by straight-forward approximation of each potential polynomial piece by a simple empirical-probability interpolation, and using plain divide-and-conquer to merge the pieces. It is universal, as well-known low-degree polynomial-approximation results imply that it accurately approximates a large class of common distributions. $\mathrm{SURF}$ is robust to distribution mis-specification as for any degree $d\le 8$, it estimates any distribution to an $\ell_1$ distance $ <3 $ times that of the nearest degree-$d$ piecewise polynomial, improving known factor upper bounds of 3 for single polynomials and 15 for polynomials with arbitrarily many pieces. It is fast, using optimal sample complexity, and running in near sample-linear time. In experiments, $\mathrm{SURF}$ significantly outperforms state-of-the art algorithms.

Unified Sample-Optimal Property Estimation in Near-Linear Time

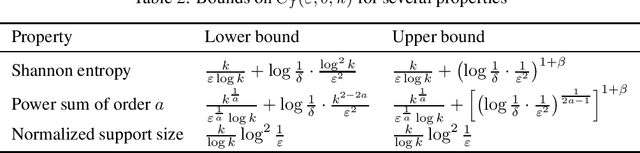
We consider the fundamental learning problem of estimating properties of distributions over large domains. Using a novel piecewise-polynomial approximation technique, we derive the first unified methodology for constructing sample- and time-efficient estimators for all sufficiently smooth, symmetric and non-symmetric, additive properties. This technique yields near-linear-time computable estimators whose approximation values are asymptotically optimal and highly-concentrated, resulting in the first: 1) estimators achieving the $\mathcal{O}(k/(\varepsilon^2\log k))$ min-max $\varepsilon$-error sample complexity for all $k$-symbol Lipschitz properties; 2) unified near-optimal differentially private estimators for a variety of properties; 3) unified estimator achieving optimal bias and near-optimal variance for five important properties; 4) near-optimal sample-complexity estimators for several important symmetric properties over both domain sizes and confidence levels. In addition, we establish a McDiarmid's inequality under Poisson sampling, which is of independent interest.

The Broad Optimality of Profile Maximum Likelihood

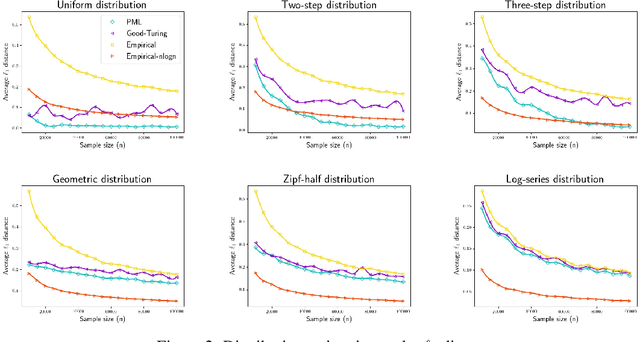
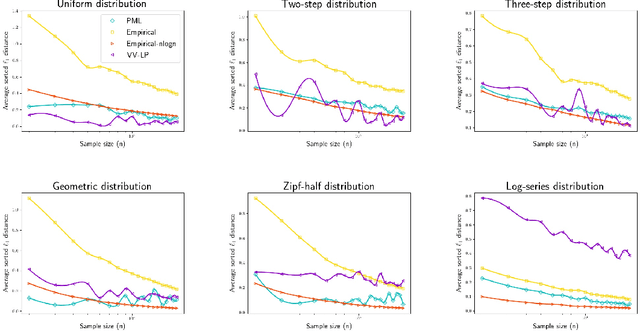
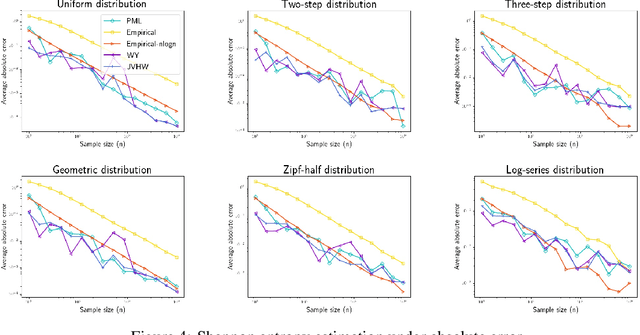
We study three fundamental statistical-learning problems: distribution estimation, property estimation, and property testing. We establish the profile maximum likelihood (PML) estimator as the first unified sample-optimal approach to a wide range of learning tasks. In particular, for every alphabet size $k$ and desired accuracy $\varepsilon$: $\textbf{Distribution estimation}$ Under $\ell_1$ distance, PML yields optimal $\Theta(k/(\varepsilon^2\log k))$ sample complexity for sorted-distribution estimation, and a PML-based estimator empirically outperforms the Good-Turing estimator on the actual distribution; $\textbf{Additive property estimation}$ For a broad class of additive properties, the PML plug-in estimator uses just four times the sample size required by the best estimator to achieve roughly twice its error, with exponentially higher confidence; $\boldsymbol{\alpha}\textbf{-R\'enyi entropy estimation}$ For integer $\alpha>1$, the PML plug-in estimator has optimal $k^{1-1/\alpha}$ sample complexity; for non-integer $\alpha>3/4$, the PML plug-in estimator has sample complexity lower than the state of the art; $\textbf{Identity testing}$ In testing whether an unknown distribution is equal to or at least $\varepsilon$ far from a given distribution in $\ell_1$ distance, a PML-based tester achieves the optimal sample complexity up to logarithmic factors of $k$. Most of these results also hold for a near-linear-time computable variant of PML. Stronger results hold for a different and novel variant called truncated PML (TPML).

Data Amplification: A Unified and Competitive Approach to Property Estimation

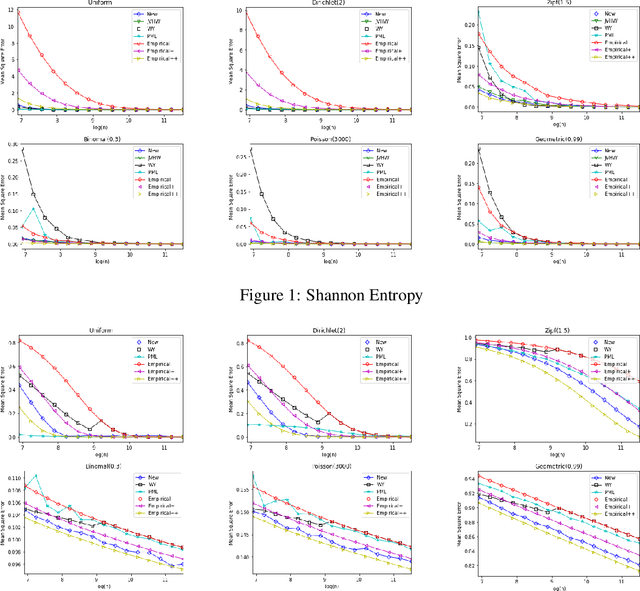
Estimating properties of discrete distributions is a fundamental problem in statistical learning. We design the first unified, linear-time, competitive, property estimator that for a wide class of properties and for all underlying distributions uses just $2n$ samples to achieve the performance attained by the empirical estimator with $n\sqrt{\log n}$ samples. This provides off-the-shelf, distribution-independent, "amplification" of the amount of data available relative to common-practice estimators. We illustrate the estimator's practical advantages by comparing it to existing estimators for a wide variety of properties and distributions. In most cases, its performance with $n$ samples is even as good as that of the empirical estimator with $n\log n$ samples, and for essentially all properties, its performance is comparable to that of the best existing estimator designed specifically for that property.

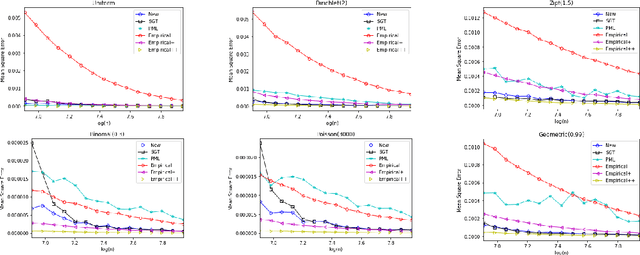
Data Amplification: Instance-Optimal Property Estimation

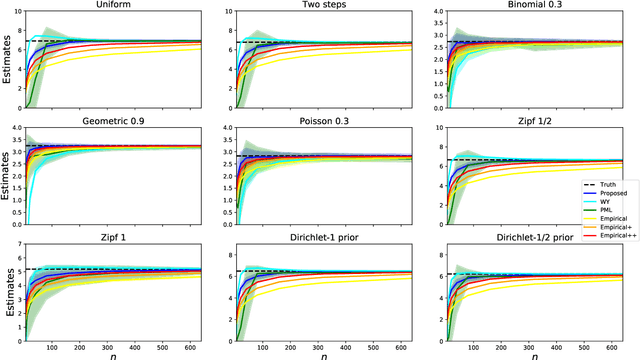
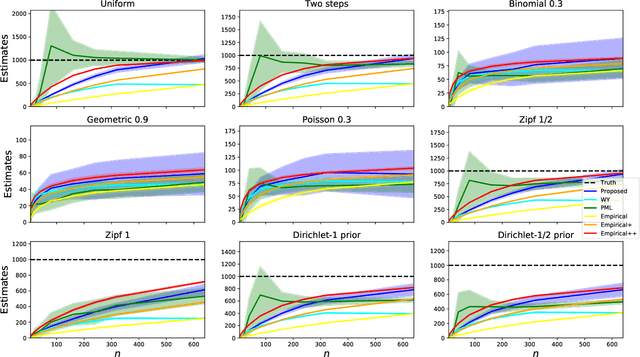
The best-known and most commonly used distribution-property estimation technique uses a plug-in estimator, with empirical frequency replacing the underlying distribution. We present novel linear-time-computable estimators that significantly "amplify" the effective amount of data available. For a large variety of distribution properties including four of the most popular ones and for every underlying distribution, they achieve the accuracy that the empirical-frequency plug-in estimators would attain using a logarithmic-factor more samples. Specifically, for Shannon entropy and a very broad class of properties including $\ell_1$-distance, the new estimators use $n$ samples to achieve the accuracy attained by the empirical estimators with $n\log n$ samples. For support-size and coverage, the new estimators use $n$ samples to achieve the performance of empirical frequency with sample size $n$ times the logarithm of the property value. Significantly strengthening the traditional min-max formulation, these results hold not only for the worst distributions, but for each and every underlying distribution. Furthermore, the logarithmic amplification factors are optimal. Experiments on a wide variety of distributions show that the new estimators outperform the previous state-of-the-art estimators designed for each specific property.

On Learning Markov Chains

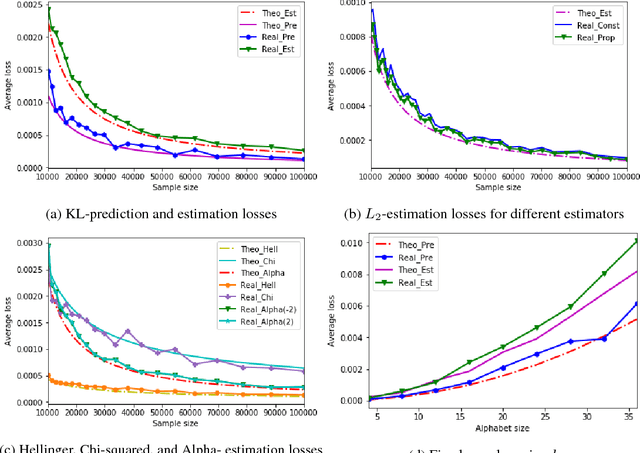
The problem of estimating an unknown discrete distribution from its samples is a fundamental tenet of statistical learning. Over the past decade, it attracted significant research effort and has been solved for a variety of divergence measures. Surprisingly, an equally important problem, estimating an unknown Markov chain from its samples, is still far from understood. We consider two problems related to the min-max risk (expected loss) of estimating an unknown $k$-state Markov chain from its $n$ sequential samples: predicting the conditional distribution of the next sample with respect to the KL-divergence, and estimating the transition matrix with respect to a natural loss induced by KL or a more general $f$-divergence measure. For the first measure, we determine the min-max prediction risk to within a linear factor in the alphabet size, showing it is $\Omega(k\log\log n\ / n)$ and $\mathcal{O}(k^2\log\log n\ / n)$. For the second, if the transition probabilities can be arbitrarily small, then only trivial uniform risk upper bounds can be derived. We therefore consider transition probabilities that are bounded away from zero, and resolve the problem for essentially all sufficiently smooth $f$-divergences, including KL-, $L_2$-, Chi-squared, Hellinger, and Alpha-divergences.