Unified Sample-Optimal Property Estimation in Near-Linear Time
Paper and Code
Nov 08, 2019
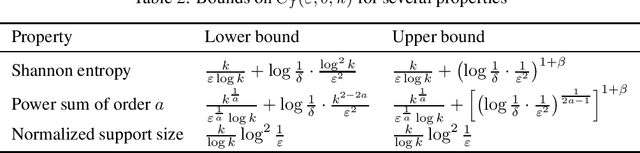
We consider the fundamental learning problem of estimating properties of distributions over large domains. Using a novel piecewise-polynomial approximation technique, we derive the first unified methodology for constructing sample- and time-efficient estimators for all sufficiently smooth, symmetric and non-symmetric, additive properties. This technique yields near-linear-time computable estimators whose approximation values are asymptotically optimal and highly-concentrated, resulting in the first: 1) estimators achieving the $\mathcal{O}(k/(\varepsilon^2\log k))$ min-max $\varepsilon$-error sample complexity for all $k$-symbol Lipschitz properties; 2) unified near-optimal differentially private estimators for a variety of properties; 3) unified estimator achieving optimal bias and near-optimal variance for five important properties; 4) near-optimal sample-complexity estimators for several important symmetric properties over both domain sizes and confidence levels. In addition, we establish a McDiarmid's inequality under Poisson sampling, which is of independent interest.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge