TURF: A Two-factor, Universal, Robust, Fast Distribution Learning Algorithm

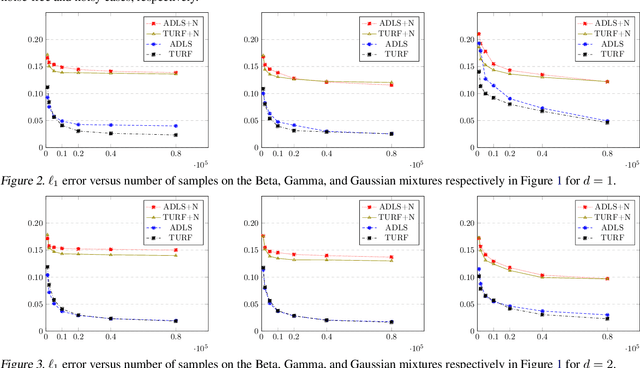
Approximating distributions from their samples is a canonical statistical-learning problem. One of its most powerful and successful modalities approximates every distribution to an $\ell_1$ distance essentially at most a constant times larger than its closest $t$-piece degree-$d$ polynomial, where $t\ge1$ and $d\ge0$. Letting $c_{t,d}$ denote the smallest such factor, clearly $c_{1,0}=1$, and it can be shown that $c_{t,d}\ge 2$ for all other $t$ and $d$. Yet current computationally efficient algorithms show only $c_{t,1}\le 2.25$ and the bound rises quickly to $c_{t,d}\le 3$ for $d\ge 9$. We derive a near-linear-time and essentially sample-optimal estimator that establishes $c_{t,d}=2$ for all $(t,d)\ne(1,0)$. Additionally, for many practical distributions, the lowest approximation distance is achieved by polynomials with vastly varying number of pieces. We provide a method that estimates this number near-optimally, hence helps approach the best possible approximation. Experiments combining the two techniques confirm improved performance over existing methodologies.

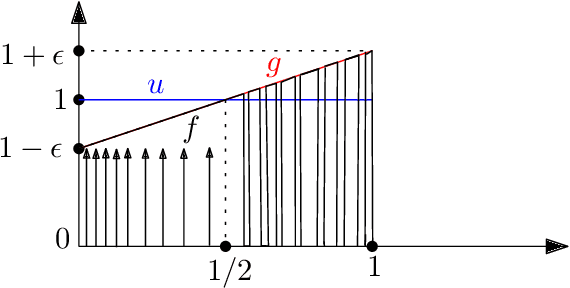
Robust estimation algorithms don't need to know the corruption level

Real data are rarely pure. Hence the past half-century has seen great interest in robust estimation algorithms that perform well even when part of the data is corrupt. However, their vast majority approach optimal accuracy only when given a tight upper bound on the fraction of corrupt data. Such bounds are not available in practice, resulting in weak guarantees and often poor performance. This brief note abstracts the complex and pervasive robustness problem into a simple geometric puzzle. It then applies the puzzle's solution to derive a universal meta technique that converts any robust estimation algorithm requiring a tight corruption-level upper bound to achieve its optimal accuracy into one achieving essentially the same accuracy without using any upper bounds.

SURF: A Simple, Universal, Robust, Fast Distribution Learning Algorithm

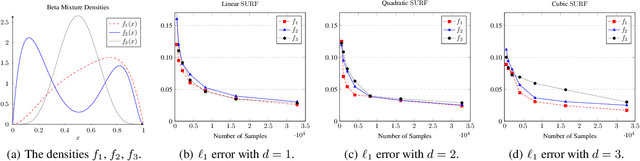
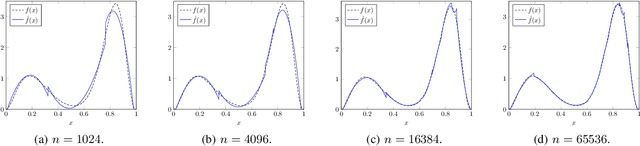
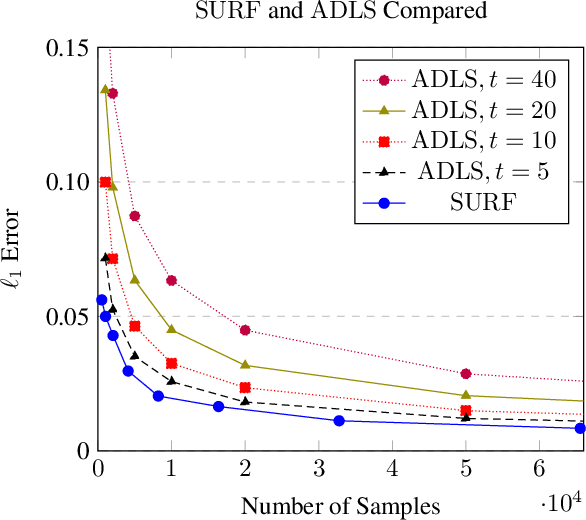
Sample- and computationally-efficient distribution estimation is a fundamental tenet in statistics and machine learning. We present $\mathrm{SURF}$, an algorithm for approximating distributions by piecewise polynomials. $\mathrm{SURF}$ is simple, replacing existing general-purpose optimization techniques by straight-forward approximation of each potential polynomial piece by a simple empirical-probability interpolation, and using plain divide-and-conquer to merge the pieces. It is universal, as well-known low-degree polynomial-approximation results imply that it accurately approximates a large class of common distributions. $\mathrm{SURF}$ is robust to distribution mis-specification as for any degree $d\le 8$, it estimates any distribution to an $\ell_1$ distance $ <3 $ times that of the nearest degree-$d$ piecewise polynomial, improving known factor upper bounds of 3 for single polynomials and 15 for polynomials with arbitrarily many pieces. It is fast, using optimal sample complexity, and running in near sample-linear time. In experiments, $\mathrm{SURF}$ significantly outperforms state-of-the art algorithms.