SURF: A Simple, Universal, Robust, Fast Distribution Learning Algorithm
Paper and Code
Feb 22, 2020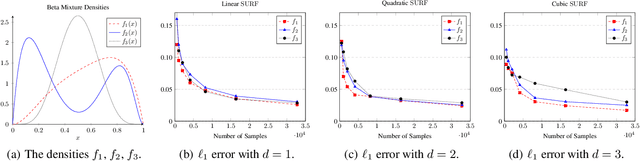
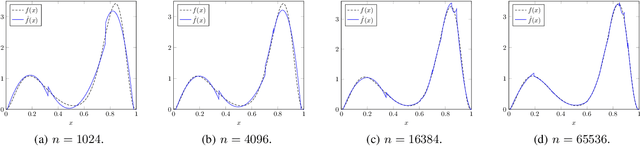
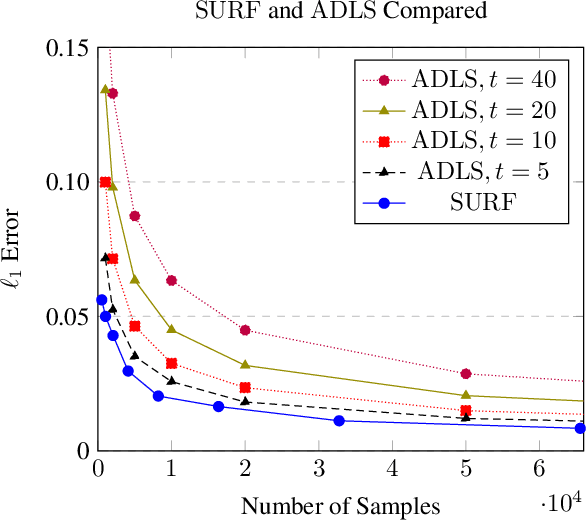

Sample- and computationally-efficient distribution estimation is a fundamental tenet in statistics and machine learning. We present $\mathrm{SURF}$, an algorithm for approximating distributions by piecewise polynomials. $\mathrm{SURF}$ is simple, replacing existing general-purpose optimization techniques by straight-forward approximation of each potential polynomial piece by a simple empirical-probability interpolation, and using plain divide-and-conquer to merge the pieces. It is universal, as well-known low-degree polynomial-approximation results imply that it accurately approximates a large class of common distributions. $\mathrm{SURF}$ is robust to distribution mis-specification as for any degree $d\le 8$, it estimates any distribution to an $\ell_1$ distance $ <3 $ times that of the nearest degree-$d$ piecewise polynomial, improving known factor upper bounds of 3 for single polynomials and 15 for polynomials with arbitrarily many pieces. It is fast, using optimal sample complexity, and running in near sample-linear time. In experiments, $\mathrm{SURF}$ significantly outperforms state-of-the art algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge