On the Emergence of Linear Analogies in Word Embeddings

Models such as Word2Vec and GloVe construct word embeddings based on the co-occurrence probability $P(i,j)$ of words $i$ and $j$ in text corpora. The resulting vectors $W_i$ not only group semantically similar words but also exhibit a striking linear analogy structure -- for example, $W_{\text{king}} - W_{\text{man}} + W_{\text{woman}} \approx W_{\text{queen}}$ -- whose theoretical origin remains unclear. Previous observations indicate that this analogy structure: (i) already emerges in the top eigenvectors of the matrix $M(i,j) = P(i,j)/P(i)P(j)$, (ii) strengthens and then saturates as more eigenvectors of $M (i, j)$, which controls the dimension of the embeddings, are included, (iii) is enhanced when using $\log M(i,j)$ rather than $M(i,j)$, and (iv) persists even when all word pairs involved in a specific analogy relation (e.g., king-queen, man-woman) are removed from the corpus. To explain these phenomena, we introduce a theoretical generative model in which words are defined by binary semantic attributes, and co-occurrence probabilities are derived from attribute-based interactions. This model analytically reproduces the emergence of linear analogy structure and naturally accounts for properties (i)-(iv). It can be viewed as giving fine-grained resolution into the role of each additional embedding dimension. It is robust to various forms of noise and agrees well with co-occurrence statistics measured on Wikipedia and the analogy benchmark introduced by Mikolov et al.

Quantum Many-Body Physics Calculations with Large Language Models

Large language models (LLMs) have demonstrated an unprecedented ability to perform complex tasks in multiple domains, including mathematical and scientific reasoning. We demonstrate that with carefully designed prompts, LLMs can accurately carry out key calculations in research papers in theoretical physics. We focus on a broadly used approximation method in quantum physics: the Hartree-Fock method, requiring an analytic multi-step calculation deriving approximate Hamiltonian and corresponding self-consistency equations. To carry out the calculations using LLMs, we design multi-step prompt templates that break down the analytic calculation into standardized steps with placeholders for problem-specific information. We evaluate GPT-4's performance in executing the calculation for 15 research papers from the past decade, demonstrating that, with correction of intermediate steps, it can correctly derive the final Hartree-Fock Hamiltonian in 13 cases and makes minor errors in 2 cases. Aggregating across all research papers, we find an average score of 87.5 (out of 100) on the execution of individual calculation steps. Overall, the requisite skill for doing these calculations is at the graduate level in quantum condensed matter theory. We further use LLMs to mitigate the two primary bottlenecks in this evaluation process: (i) extracting information from papers to fill in templates and (ii) automatic scoring of the calculation steps, demonstrating good results in both cases. The strong performance is the first step for developing algorithms that automatically explore theoretical hypotheses at an unprecedented scale.

Les Houches Lectures on Deep Learning at Large & Infinite Width

These lectures, presented at the 2022 Les Houches Summer School on Statistical Physics and Machine Learning, focus on the infinite-width limit and large-width regime of deep neural networks. Topics covered include various statistical and dynamical properties of these networks. In particular, the lecturers discuss properties of random deep neural networks; connections between trained deep neural networks, linear models, kernels, and Gaussian processes that arise in the infinite-width limit; and perturbative and non-perturbative treatments of large but finite-width networks, at initialization and after training.

Beyond the Imitation Game: Quantifying and extrapolating the capabilities of language models

Language models demonstrate both quantitative improvement and new qualitative capabilities with increasing scale. Despite their potentially transformative impact, these new capabilities are as yet poorly characterized. In order to inform future research, prepare for disruptive new model capabilities, and ameliorate socially harmful effects, it is vital that we understand the present and near-future capabilities and limitations of language models. To address this challenge, we introduce the Beyond the Imitation Game benchmark (BIG-bench). BIG-bench currently consists of 204 tasks, contributed by 442 authors across 132 institutions. Task topics are diverse, drawing problems from linguistics, childhood development, math, common-sense reasoning, biology, physics, social bias, software development, and beyond. BIG-bench focuses on tasks that are believed to be beyond the capabilities of current language models. We evaluate the behavior of OpenAI's GPT models, Google-internal dense transformer architectures, and Switch-style sparse transformers on BIG-bench, across model sizes spanning millions to hundreds of billions of parameters. In addition, a team of human expert raters performed all tasks in order to provide a strong baseline. Findings include: model performance and calibration both improve with scale, but are poor in absolute terms (and when compared with rater performance); performance is remarkably similar across model classes, though with benefits from sparsity; tasks that improve gradually and predictably commonly involve a large knowledge or memorization component, whereas tasks that exhibit "breakthrough" behavior at a critical scale often involve multiple steps or components, or brittle metrics; social bias typically increases with scale in settings with ambiguous context, but this can be improved with prompting.

The Evolution of Out-of-Distribution Robustness Throughout Fine-Tuning

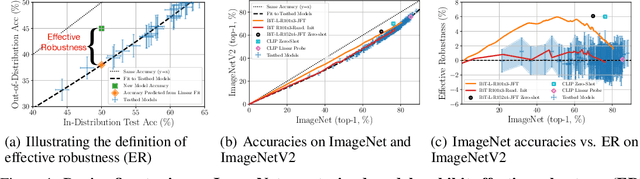
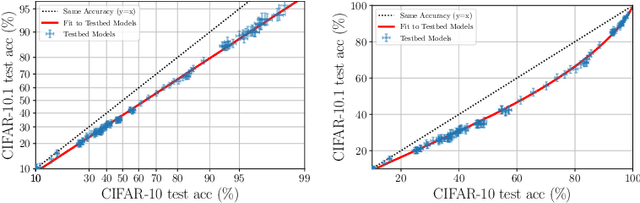
Although machine learning models typically experience a drop in performance on out-of-distribution data, accuracies on in- versus out-of-distribution data are widely observed to follow a single linear trend when evaluated across a testbed of models. Models that are more accurate on the out-of-distribution data relative to this baseline exhibit "effective robustness" and are exceedingly rare. Identifying such models, and understanding their properties, is key to improving out-of-distribution performance. We conduct a thorough empirical investigation of effective robustness during fine-tuning and surprisingly find that models pre-trained on larger datasets exhibit effective robustness during training that vanishes at convergence. We study how properties of the data influence effective robustness, and we show that it increases with the larger size, more diversity, and higher example difficulty of the dataset. We also find that models that display effective robustness are able to correctly classify 10% of the examples that no other current testbed model gets correct. Finally, we discuss several strategies for scaling effective robustness to the high-accuracy regime to improve the out-of-distribution accuracy of state-of-the-art models.

Explaining Neural Scaling Laws

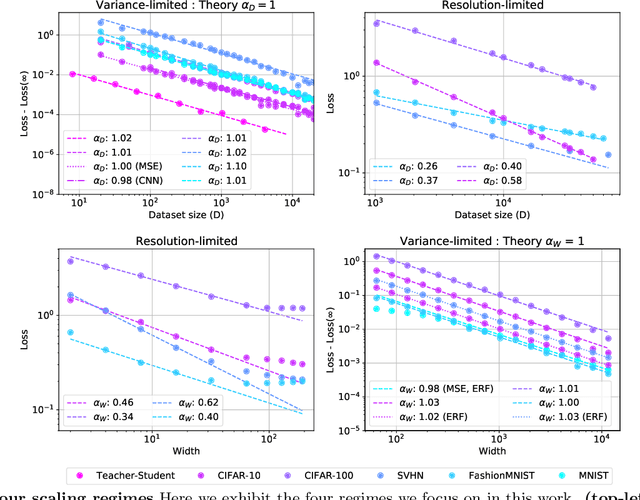
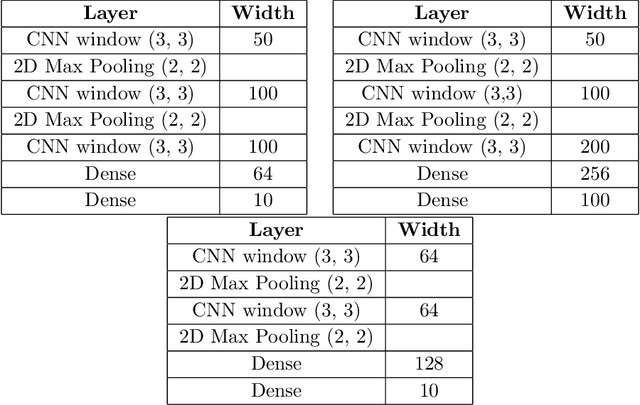
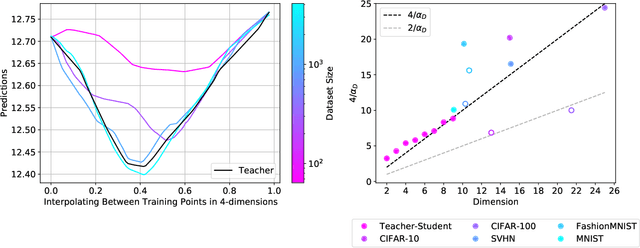
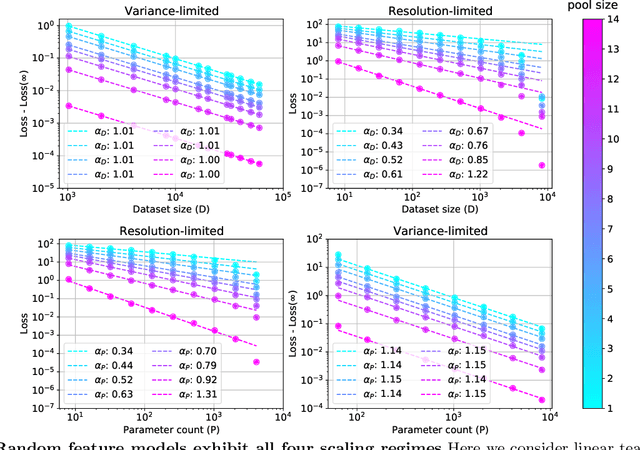
The test loss of well-trained neural networks often follows precise power-law scaling relations with either the size of the training dataset or the number of parameters in the network. We propose a theory that explains and connects these scaling laws. We identify variance-limited and resolution-limited scaling behavior for both dataset and model size, for a total of four scaling regimes. The variance-limited scaling follows simply from the existence of a well-behaved infinite data or infinite width limit, while the resolution-limited regime can be explained by positing that models are effectively resolving a smooth data manifold. In the large width limit, this can be equivalently obtained from the spectrum of certain kernels, and we present evidence that large width and large dataset resolution-limited scaling exponents are related by a duality. We exhibit all four scaling regimes in the controlled setting of large random feature and pretrained models and test the predictions empirically on a range of standard architectures and datasets. We also observe several empirical relationships between datasets and scaling exponents: super-classing image tasks does not change exponents, while changing input distribution (via changing datasets or adding noise) has a strong effect. We further explore the effect of architecture aspect ratio on scaling exponents.

Exact posterior distributions of wide Bayesian neural networks

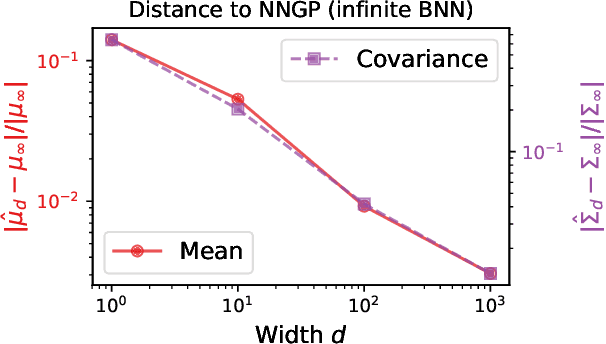
Recent work has shown that the prior over functions induced by a deep Bayesian neural network (BNN) behaves as a Gaussian process (GP) as the width of all layers becomes large. However, many BNN applications are concerned with the BNN function space posterior. While some empirical evidence of the posterior convergence was provided in the original works of Neal (1996) and Matthews et al. (2018), it is limited to small datasets or architectures due to the notorious difficulty of obtaining and verifying exactness of BNN posterior approximations. We provide the missing theoretical proof that the exact BNN posterior converges (weakly) to the one induced by the GP limit of the prior. For empirical validation, we show how to generate exact samples from a finite BNN on a small dataset via rejection sampling.

Infinite attention: NNGP and NTK for deep attention networks

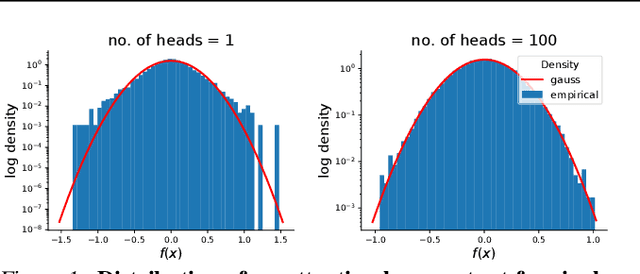
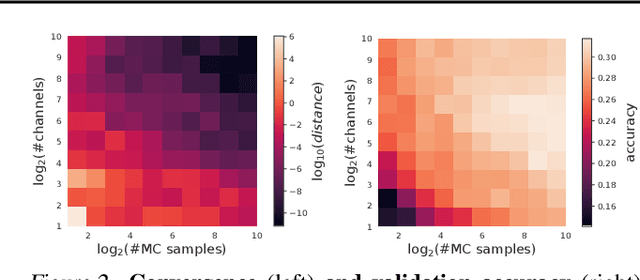
There is a growing amount of literature on the relationship between wide neural networks (NNs) and Gaussian processes (GPs), identifying an equivalence between the two for a variety of NN architectures. This equivalence enables, for instance, accurate approximation of the behaviour of wide Bayesian NNs without MCMC or variational approximations, or characterisation of the distribution of randomly initialised wide NNs optimised by gradient descent without ever running an optimiser. We provide a rigorous extension of these results to NNs involving attention layers, showing that unlike single-head attention, which induces non-Gaussian behaviour, multi-head attention architectures behave as GPs as the number of heads tends to infinity. We further discuss the effects of positional encodings and layer normalisation, and propose modifications of the attention mechanism which lead to improved results for both finite and infinitely wide NNs. We evaluate attention kernels empirically, leading to a moderate improvement upon the previous state-of-the-art on CIFAR-10 for GPs without trainable kernels and advanced data preprocessing. Finally, we introduce new features to the Neural Tangents library (Novak et al., 2020) allowing applications of NNGP/NTK models, with and without attention, to variable-length sequences, with an example on the IMDb reviews dataset.

The large learning rate phase of deep learning: the catapult mechanism

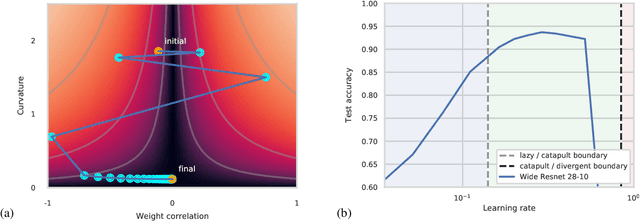
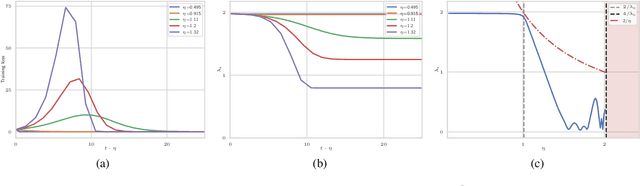
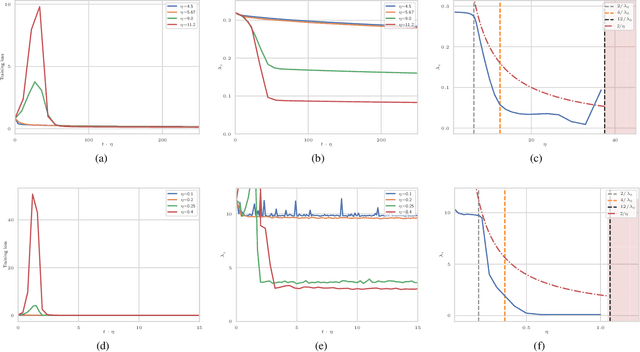
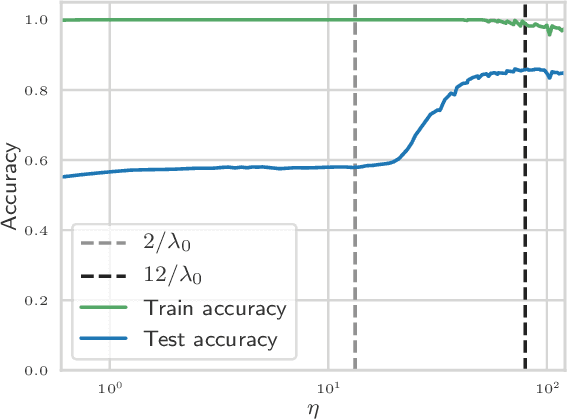
The choice of initial learning rate can have a profound effect on the performance of deep networks. We present a class of neural networks with solvable training dynamics, and confirm their predictions empirically in practical deep learning settings. The networks exhibit sharply distinct behaviors at small and large learning rates. The two regimes are separated by a phase transition. In the small learning rate phase, training can be understood using the existing theory of infinitely wide neural networks. At large learning rates the model captures qualitatively distinct phenomena, including the convergence of gradient descent dynamics to flatter minima. One key prediction of our model is a narrow range of large, stable learning rates. We find good agreement between our model's predictions and training dynamics in realistic deep learning settings. Furthermore, we find that the optimal performance in such settings is often found in the large learning rate phase. We believe our results shed light on characteristics of models trained at different learning rates. In particular, they fill a gap between existing wide neural network theory, and the nonlinear, large learning rate, training dynamics relevant to practice.

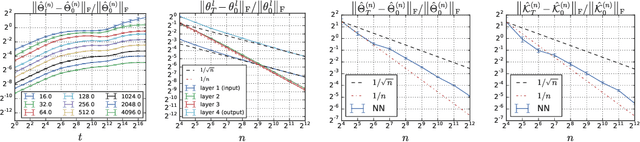
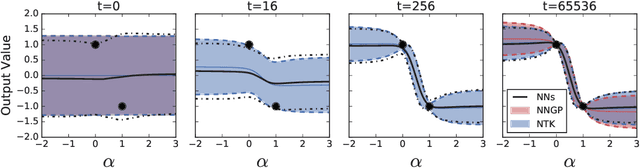
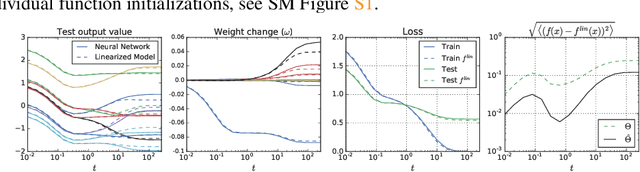
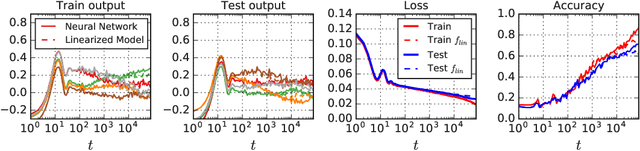
Wide Neural Networks of Any Depth Evolve as Linear Models Under Gradient Descent

A longstanding goal in deep learning research has been to precisely characterize training and generalization. However, the often complex loss landscapes of neural networks have made a theory of learning dynamics elusive. In this work, we show that for wide neural networks the learning dynamics simplify considerably and that, in the infinite width limit, they are governed by a linear model obtained from the first-order Taylor expansion of the network around its initial parameters. Furthermore, mirroring the correspondence between wide Bayesian neural networks and Gaussian processes, gradient-based training of wide neural networks with a squared loss produces test set predictions drawn from a Gaussian process with a particular compositional kernel. While these theoretical results are only exact in the infinite width limit, we nevertheless find excellent empirical agreement between the predictions of the original network and those of the linearized version even for finite practically-sized networks. This agreement is robust across different architectures, optimization methods, and loss functions.