Guided Flows for Generative Modeling and Decision Making

Classifier-free guidance is a key component for enhancing the performance of conditional generative models across diverse tasks. While it has previously demonstrated remarkable improvements for the sample quality, it has only been exclusively employed for diffusion models. In this paper, we integrate classifier-free guidance into Flow Matching (FM) models, an alternative simulation-free approach that trains Continuous Normalizing Flows (CNFs) based on regressing vector fields. We explore the usage of \emph{Guided Flows} for a variety of downstream applications. We show that Guided Flows significantly improves the sample quality in conditional image generation and zero-shot text-to-speech synthesis, boasting state-of-the-art performance. Notably, we are the first to apply flow models for plan generation in the offline reinforcement learning setting, showcasing a 10x speedup in computation compared to diffusion models while maintaining comparable performance.

Bespoke Solvers for Generative Flow Models

Diffusion or flow-based models are powerful generative paradigms that are notoriously hard to sample as samples are defined as solutions to high-dimensional Ordinary or Stochastic Differential Equations (ODEs/SDEs) which require a large Number of Function Evaluations (NFE) to approximate well. Existing methods to alleviate the costly sampling process include model distillation and designing dedicated ODE solvers. However, distillation is costly to train and sometimes can deteriorate quality, while dedicated solvers still require relatively large NFE to produce high quality samples. In this paper we introduce "Bespoke solvers", a novel framework for constructing custom ODE solvers tailored to the ODE of a given pre-trained flow model. Our approach optimizes an order consistent and parameter-efficient solver (e.g., with 80 learnable parameters), is trained for roughly 1% of the GPU time required for training the pre-trained model, and significantly improves approximation and generation quality compared to dedicated solvers. For example, a Bespoke solver for a CIFAR10 model produces samples with Fr\'echet Inception Distance (FID) of 2.73 with 10 NFE, and gets to 1% of the Ground Truth (GT) FID (2.59) for this model with only 20 NFE. On the more challenging ImageNet-64$\times$64, Bespoke samples at 2.2 FID with 10 NFE, and gets within 2% of GT FID (1.71) with 20 NFE.

Generalized Schrödinger Bridge Matching

Modern distribution matching algorithms for training diffusion or flow models directly prescribe the time evolution of the marginal distributions between two boundary distributions. In this work, we consider a generalized distribution matching setup, where these marginals are only implicitly described as a solution to some task-specific objective function. The problem setup, known as the Generalized Schr\"odinger Bridge (GSB), appears prevalently in many scientific areas both within and without machine learning. We propose Generalized Schr\"odinger Bridge Matching (GSBM), a new matching algorithm inspired by recent advances, generalizing them beyond kinetic energy minimization and to account for task-specific state costs. We show that such a generalization can be cast as solving conditional stochastic optimal control, for which efficient variational approximations can be used, and further debiased with the aid of path integral theory. Compared to prior methods for solving GSB problems, our GSBM algorithm always preserves a feasible transport map between the boundary distributions throughout training, thereby enabling stable convergence and significantly improved scalability. We empirically validate our claims on an extensive suite of experimental setups, including crowd navigation, opinion depolarization, LiDAR manifolds, and image domain transfer. Our work brings new algorithmic opportunities for training diffusion models enhanced with task-specific optimality structures.

On Kinetic Optimal Probability Paths for Generative Models

Recent successful generative models are trained by fitting a neural network to an a-priori defined tractable probability density path taking noise to training examples. In this paper we investigate the space of Gaussian probability paths, which includes diffusion paths as an instance, and look for an optimal member in some useful sense. In particular, minimizing the Kinetic Energy (KE) of a path is known to make particles' trajectories simple, hence easier to sample, and empirically improve performance in terms of likelihood of unseen data and sample generation quality. We investigate Kinetic Optimal (KO) Gaussian paths and offer the following observations: (i) We show the KE takes a simplified form on the space of Gaussian paths, where the data is incorporated only through a single, one dimensional scalar function, called the \emph{data separation function}. (ii) We characterize the KO solutions with a one dimensional ODE. (iii) We approximate data-dependent KO paths by approximating the data separation function and minimizing the KE. (iv) We prove that the data separation function converges to $1$ in the general case of arbitrary normalized dataset consisting of $n$ samples in $d$ dimension as $n/\sqrt{d}\rightarrow 0$. A consequence of this result is that the Conditional Optimal Transport (Cond-OT) path becomes \emph{kinetic optimal} as $n/\sqrt{d}\rightarrow 0$. We further support this theory with empirical experiments on ImageNet.

Multisample Flow Matching: Straightening Flows with Minibatch Couplings

Simulation-free methods for training continuous-time generative models construct probability paths that go between noise distributions and individual data samples. Recent works, such as Flow Matching, derived paths that are optimal for each data sample. However, these algorithms rely on independent data and noise samples, and do not exploit underlying structure in the data distribution for constructing probability paths. We propose Multisample Flow Matching, a more general framework that uses non-trivial couplings between data and noise samples while satisfying the correct marginal constraints. At very small overhead costs, this generalization allows us to (i) reduce gradient variance during training, (ii) obtain straighter flows for the learned vector field, which allows us to generate high-quality samples using fewer function evaluations, and (iii) obtain transport maps with lower cost in high dimensions, which has applications beyond generative modeling. Importantly, we do so in a completely simulation-free manner with a simple minimization objective. We show that our proposed methods improve sample consistency on downsampled ImageNet data sets, and lead to better low-cost sample generation.

VisCo Grids: Surface Reconstruction with Viscosity and Coarea Grids

Surface reconstruction has been seeing a lot of progress lately by utilizing Implicit Neural Representations (INRs). Despite their success, INRs often introduce hard to control inductive bias (i.e., the solution surface can exhibit unexplainable behaviours), have costly inference, and are slow to train. The goal of this work is to show that replacing neural networks with simple grid functions, along with two novel geometric priors achieve comparable results to INRs, with instant inference, and improved training times. To that end we introduce VisCo Grids: a grid-based surface reconstruction method incorporating Viscosity and Coarea priors. Intuitively, the Viscosity prior replaces the smoothness inductive bias of INRs, while the Coarea favors a minimal area solution. Experimenting with VisCo Grids on a standard reconstruction baseline provided comparable results to the best performing INRs on this dataset.

Equivariant Polynomials for Graph Neural Networks

Graph Neural Networks (GNN) are inherently limited in their expressive power. Recent seminal works (Xu et al., 2019; Morris et al., 2019b) introduced the Weisfeiler-Lehman (WL) hierarchy as a measure of expressive power. Although this hierarchy has propelled significant advances in GNN analysis and architecture developments, it suffers from several significant limitations. These include a complex definition that lacks direct guidance for model improvement and a WL hierarchy that is too coarse to study current GNNs. This paper introduces an alternative expressive power hierarchy based on the ability of GNNs to calculate equivariant polynomials of a certain degree. As a first step, we provide a full characterization of all equivariant graph polynomials by introducing a concrete basis, significantly generalizing previous results. Each basis element corresponds to a specific multi-graph, and its computation over some graph data input corresponds to a tensor contraction problem. Second, we propose algorithmic tools for evaluating the expressiveness of GNNs using tensor contraction sequences, and calculate the expressive power of popular GNNs. Finally, we enhance the expressivity of common GNN architectures by adding polynomial features or additional operations / aggregations inspired by our theory. These enhanced GNNs demonstrate state-of-the-art results in experiments across multiple graph learning benchmarks.

MultiDiffusion: Fusing Diffusion Paths for Controlled Image Generation

Recent advances in text-to-image generation with diffusion models present transformative capabilities in image quality. However, user controllability of the generated image, and fast adaptation to new tasks still remains an open challenge, currently mostly addressed by costly and long re-training and fine-tuning or ad-hoc adaptations to specific image generation tasks. In this work, we present MultiDiffusion, a unified framework that enables versatile and controllable image generation, using a pre-trained text-to-image diffusion model, without any further training or finetuning. At the center of our approach is a new generation process, based on an optimization task that binds together multiple diffusion generation processes with a shared set of parameters or constraints. We show that MultiDiffusion can be readily applied to generate high quality and diverse images that adhere to user-provided controls, such as desired aspect ratio (e.g., panorama), and spatial guiding signals, ranging from tight segmentation masks to bounding boxes. Project webpage: https://multidiffusion.github.io

Riemannian Flow Matching on General Geometries

We propose Riemannian Flow Matching (RFM), a simple yet powerful framework for training continuous normalizing flows on manifolds. Existing methods for generative modeling on manifolds either require expensive simulation, inherently cannot scale to high dimensions, or use approximations to limiting quantities that result in biased objectives. Riemannian Flow Matching bypasses these inconveniences and exhibits multiple benefits over prior approaches: It is completely simulation-free on simple geometries, it does not require divergence computation, and its target vector field is computed in closed form even on general geometries. The key ingredient behind RFM is the construction of a simple kernel function for defining per-sample vector fields, which subsumes existing Euclidean cases. Extending to general geometries, we rely on the use of spectral decompositions to efficiently compute kernel functions. Our method achieves state-of-the-art performance on real-world non-Euclidean datasets, and we showcase, for the first time, tractable training on general geometries, including on triangular meshes and maze-like manifolds with boundaries.

Flow Matching for Generative Modeling

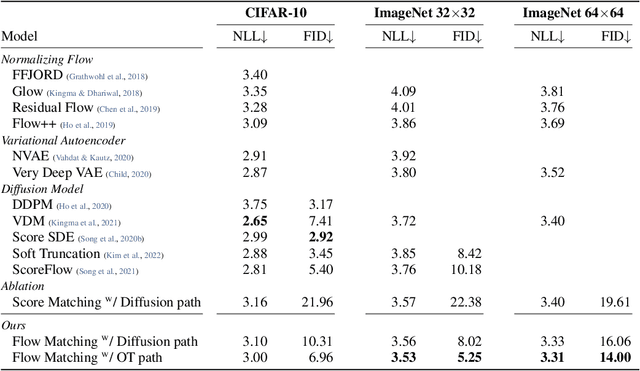
We introduce a new paradigm for generative modeling built on Continuous Normalizing Flows (CNFs), allowing us to train CNFs at unprecedented scale. Specifically, we present the notion of Flow Matching (FM), a simulation-free approach for training CNFs based on regressing vector fields of fixed conditional probability paths. Flow Matching is compatible with a general family of Gaussian probability paths for transforming between noise and data samples -- which subsumes existing diffusion paths as specific instances. Interestingly, we find that employing FM with diffusion paths results in a more robust and stable alternative for training diffusion models. Furthermore, Flow Matching opens the door to training CNFs with other, non-diffusion probability paths. An instance of particular interest is using Optimal Transport (OT) displacement interpolation to define the conditional probability paths. These paths are more efficient than diffusion paths, provide faster training and sampling, and result in better generalization. Training CNFs using Flow Matching on ImageNet leads to state-of-the-art performance in terms of both likelihood and sample quality, and allows fast and reliable sample generation using off-the-shelf numerical ODE solvers.