Weisfeiler and Leman Go Gambling: Why Expressive Lottery Tickets Win

The lottery ticket hypothesis (LTH) is well-studied for convolutional neural networks but has been validated only empirically for graph neural networks (GNNs), for which theoretical findings are largely lacking. In this paper, we identify the expressivity of sparse subnetworks, i.e. their ability to distinguish non-isomorphic graphs, as crucial for finding winning tickets that preserve the predictive performance. We establish conditions under which the expressivity of a sparsely initialized GNN matches that of the full network, particularly when compared to the Weisfeiler-Leman test, and in that context put forward and prove a Strong Expressive Lottery Ticket Hypothesis. We subsequently show that an increased expressivity in the initialization potentially accelerates model convergence and improves generalization. Our findings establish novel theoretical foundations for both LTH and GNN research, highlighting the importance of maintaining expressivity in sparsely initialized GNNs. We illustrate our results using examples from drug discovery.

Efficient Mixed Precision Quantization in Graph Neural Networks

Graph Neural Networks (GNNs) have become essential for handling large-scale graph applications. However, the computational demands of GNNs necessitate the development of efficient methods to accelerate inference. Mixed precision quantization emerges as a promising solution to enhance the efficiency of GNN architectures without compromising prediction performance. Compared to conventional deep learning architectures, GNN layers contain a wider set of components that can be quantized, including message passing functions, aggregation functions, update functions, the inputs, learnable parameters, and outputs of these functions. In this paper, we introduce a theorem for efficient quantized message passing to aggregate integer messages. It guarantees numerical equality of the aggregated messages using integer values with respect to those obtained with full (FP32) precision. Based on this theorem, we introduce the Mixed Precision Quantization for GNN (MixQ-GNN) framework, which flexibly selects effective integer bit-widths for all components within GNN layers. Our approach systematically navigates the wide set of possible bit-width combinations, addressing the challenge of optimizing efficiency while aiming at maintaining comparable prediction performance. MixQ-GNN integrates with existing GNN quantization methods, utilizing their graph structure advantages to achieve higher prediction performance. On average, MixQ-GNN achieved reductions in bit operations of 5.5x for node classification and 5.1x for graph classification compared to architectures represented in FP32 precision.

On the Relationship Between Robustness and Expressivity of Graph Neural Networks

We investigate the vulnerability of Graph Neural Networks (GNNs) to bit-flip attacks (BFAs) by introducing an analytical framework to study the influence of architectural features, graph properties, and their interaction. The expressivity of GNNs refers to their ability to distinguish non-isomorphic graphs and depends on the encoding of node neighborhoods. We examine the vulnerability of neural multiset functions commonly used for this purpose and establish formal criteria to characterize a GNN's susceptibility to losing expressivity due to BFAs. This enables an analysis of the impact of homophily, graph structural variety, feature encoding, and activation functions on GNN robustness. We derive theoretical bounds for the number of bit flips required to degrade GNN expressivity on a dataset, identifying ReLU-activated GNNs operating on highly homophilous graphs with low-dimensional or one-hot encoded features as particularly susceptible. Empirical results using ten real-world datasets confirm the statistical significance of our key theoretical insights and offer actionable results to mitigate BFA risks in expressivity-critical applications.

Preventing Representational Rank Collapse in MPNNs by Splitting the Computational Graph

The ability of message-passing neural networks (MPNNs) to fit complex functions over graphs is limited each iteration of message-passing over a simple makes representations more similar, a phenomenon known as rank collapse, and over-smoothing as a special case. Most approaches to mitigate over-smoothing extend common message-passing schemes, e.g., the graph convolutional network, by utilizing residual connections, gating mechanisms, normalization, or regularization techniques. Our work contrarily proposes to directly tackle the cause of this issue by modifying the message-passing scheme and exchanging different types of messages using multi-relational graphs. We identify the necessary and sufficient condition to ensure linearly independent node representations. As one instantion, we show that operating on multiple directed acyclic graphs always satisfies our condition and propose to obtain these by defining a strict partial ordering of the nodes. We conduct comprehensive experiments that confirm the benefits of operating on multi-relational graphs to achieve more informative node representations.

Non-Redundant Graph Neural Networks with Improved Expressiveness

Message passing graph neural networks iteratively compute node embeddings by aggregating messages from all neighbors. This procedure can be viewed as a neural variant of the Weisfeiler-Leman method, which limits their expressive power. Moreover, oversmoothing and oversquashing restrict the number of layers these networks can effectively utilize. The repeated exchange and encoding of identical information in message passing amplifies oversquashing. We propose a novel aggregation scheme based on neighborhood trees, which allows for controlling the redundancy by pruning branches of the unfolding trees underlying standard message passing. We prove that reducing redundancy improves expressivity and experimentally show that it alleviates oversquashing. We investigate the interaction between redundancy in message passing and redundancy in computation and propose a compact representation of neighborhood trees, from which we compute node and graph embeddings via a neural tree canonization technique. Our method is provably more expressive than the Weisfeiler-Leman method, less susceptible to oversquashing than message passing neural networks, and provides high classification accuracy on widely-used benchmark datasets.

Gradual Weisfeiler-Leman: Slow and Steady Wins the Race

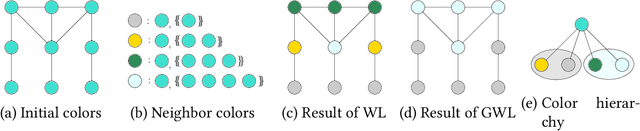
The classical Weisfeiler-Leman algorithm aka color refinement is fundamental for graph learning and central for successful graph kernels and graph neural networks. Originally developed for graph isomorphism testing, the algorithm iteratively refines vertex colors. On many datasets, the stable coloring is reached after a few iterations and the optimal number of iterations for machine learning tasks is typically even lower. This suggests that the colors diverge too fast, defining a similarity that is too coarse. We generalize the concept of color refinement and propose a framework for gradual neighborhood refinement, which allows a slower convergence to the stable coloring and thus provides a more fine-grained refinement hierarchy and vertex similarity. We assign new colors by clustering vertex neighborhoods, replacing the original injective color assignment function. Our approach is used to derive new variants of existing graph kernels and to approximate the graph edit distance via optimal assignments regarding vertex similarity. We show that in both tasks, our method outperforms the original color refinement with only moderate increase in running time advancing the state of the art.

A Temporal Graphlet Kernel for Classifying Dissemination in Evolving Networks

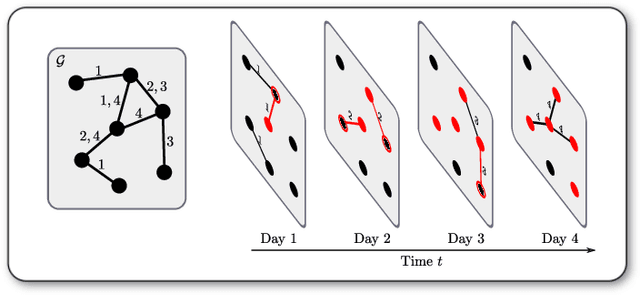
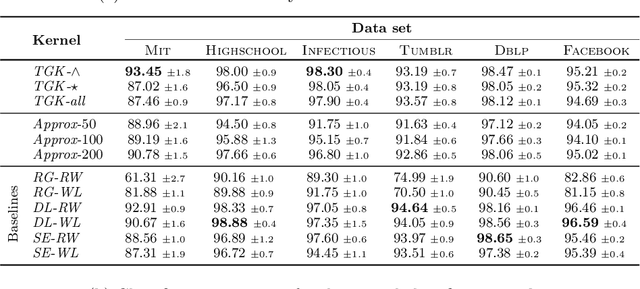
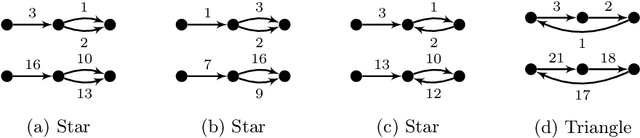
We introduce the \emph{temporal graphlet kernel} for classifying dissemination processes in labeled temporal graphs. Such dissemination processes can be spreading (fake) news, infectious diseases, or computer viruses in dynamic networks. The networks are modeled as labeled temporal graphs, in which the edges exist at specific points in time, and node labels change over time. The classification problem asks to discriminate dissemination processes of different origins or parameters, e.g., infectious diseases with different infection probabilities. Our new kernel represents labeled temporal graphs in the feature space of temporal graphlets, i.e., small subgraphs distinguished by their structure, time-dependent node labels, and chronological order of edges. We introduce variants of our kernel based on classes of graphlets that are efficiently countable. For the case of temporal wedges, we propose a highly efficient approximative kernel with low error in expectation. We show that our kernels are faster to compute and provide better accuracy than state-of-the-art methods.

Weisfeiler and Leman Go Walking: Random Walk Kernels Revisited

Random walk kernels have been introduced in seminal work on graph learning and were later largely superseded by kernels based on the Weisfeiler-Leman test for graph isomorphism. We give a unified view on both classes of graph kernels. We study walk-based node refinement methods and formally relate them to several widely-used techniques, including Morgan's algorithm for molecule canonization and the Weisfeiler-Leman test. We define corresponding walk-based kernels on nodes that allow fine-grained parameterized neighborhood comparison, reach Weisfeiler-Leman expressiveness, and are computed using the kernel trick. From this we show that classical random walk kernels with only minor modifications regarding definition and computation are as expressive as the widely-used Weisfeiler-Leman subtree kernel but support non-strict neighborhood comparison. We verify experimentally that walk-based kernels reach or even surpass the accuracy of Weisfeiler-Leman kernels in real-world classification tasks.

Temporal Walk Centrality: Ranking Nodes in Evolving Networks

We propose the Temporal Walk Centrality, which quantifies the importance of a node by measuring its ability to obtain and distribute information in a temporal network. In contrast to the widely-used betweenness centrality, we assume that information does not necessarily spread on shortest paths but on temporal random walks that satisfy the time constraints of the network. We show that temporal walk centrality can identify nodes playing central roles in dissemination processes that might not be detected by related betweenness concepts and other common static and temporal centrality measures. We propose exact and approximation algorithms with different running times depending on the properties of the temporal network and parameters of our new centrality measure. A technical contribution is a general approach to lift existing algebraic methods for counting walks in static networks to temporal networks. Our experiments on real-world temporal networks show the efficiency and accuracy of our algorithms. Finally, we demonstrate that the rankings by temporal walk centrality often differ significantly from those of other state-of-the-art temporal centralities.

Weisfeiler and Leman go Machine Learning: The Story so far

In recent years, algorithms and neural architectures based on the Weisfeiler-Leman algorithm, a well-known heuristic for the graph isomorphism problem, emerged as a powerful tool for machine learning with graphs and relational data. Here, we give a comprehensive overview of the algorithm's use in a machine learning setting, focusing on the supervised regime. We discuss the theoretical background, show how to use it for supervised graph- and node representation learning, discuss recent extensions, and outline the algorithm's connection to (permutation-)equivariant neural architectures. Moreover, we give an overview of current applications and future directions to stimulate further research.