A Bayesian approach to learning mixtures of nonparametric components

Mixture models are widely used in modeling heterogeneous data populations. A standard approach of mixture modeling is to assume that the mixture component takes a parametric kernel form, while the flexibility of the model can be obtained by using a large or possibly unbounded number of such parametric kernels. In many applications, making parametric assumptions on the latent subpopulation distributions may be unrealistic, which motivates the need for nonparametric modeling of the mixture components themselves. In this paper we study finite mixtures with nonparametric mixture components, using a Bayesian nonparametric modeling approach. In particular, it is assumed that the data population is generated according to a finite mixture of latent component distributions, where each component is endowed with a Bayesian nonparametric prior such as the Dirichlet process mixture. We present conditions under which the individual mixture component's distributions can be identified, and establish posterior contraction behavior for the data population's density, as well as densities of the latent mixture components. We develop an efficient MCMC algorithm for posterior inference and demonstrate via simulation studies and real-world data illustrations that it is possible to efficiently learn complex distributions for the latent subpopulations. In theory, the posterior contraction rate of the component densities is nearly polynomial, which is a significant improvement over the logarithm convergence rate of estimating mixing measures via deconvolution.

Dendrogram of mixing measures: Hierarchical clustering and model selection for finite mixture models

We present a new way to summarize and select mixture models via the hierarchical clustering tree (dendrogram) constructed from an overfitted latent mixing measure. Our proposed method bridges agglomerative hierarchical clustering and mixture modeling. The dendrogram's construction is derived from the theory of convergence of the mixing measures, and as a result, we can both consistently select the true number of mixing components and obtain the pointwise optimal convergence rate for parameter estimation from the tree, even when the model parameters are only weakly identifiable. In theory, it explicates the choice of the optimal number of clusters in hierarchical clustering. In practice, the dendrogram reveals more information on the hierarchy of subpopulations compared to traditional ways of summarizing mixture models. Several simulation studies are carried out to support our theory. We also illustrate the methodology with an application to single-cell RNA sequence analysis.

Strong identifiability and parameter learning in regression with heterogeneous response

Mixtures of regression are a powerful class of models for regression learning with respect to a highly uncertain and heterogeneous response variable of interest. In addition to being a rich predictive model for the response given some covariates, the parameters in this model class provide useful information about the heterogeneity in the data population, which is represented by the conditional distributions for the response given the covariates associated with a number of distinct but latent subpopulations. In this paper, we investigate conditions of strong identifiability, rates of convergence for conditional density and parameter estimation, and the Bayesian posterior contraction behavior arising in finite mixture of regression models, under exact-fitted and over-fitted settings and when the number of components is unknown. This theory is applicable to common choices of link functions and families of conditional distributions employed by practitioners. We provide simulation studies and data illustrations, which shed some light on the parameter learning behavior found in several popular regression mixture models reported in the literature.

Beyond Black Box Densities: Parameter Learning for the Deviated Components

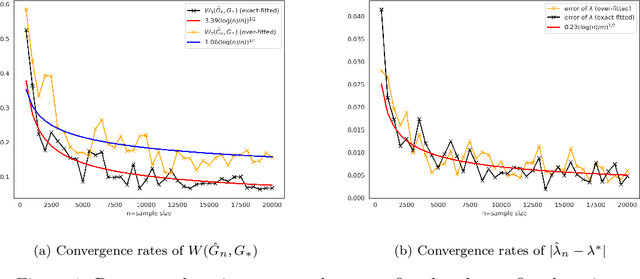
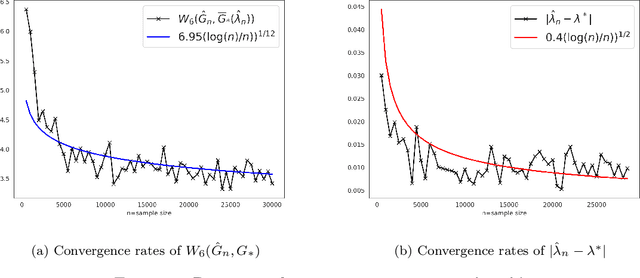
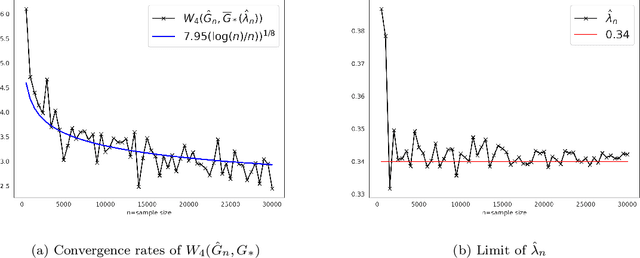
As we collect additional samples from a data population for which a known density function estimate may have been previously obtained by a black box method, the increased complexity of the data set may result in the true density being deviated from the known estimate by a mixture distribution. To model this phenomenon, we consider the \emph{deviating mixture model} $(1-\lambda^{*})h_0 + \lambda^{*} (\sum_{i = 1}^{k} p_{i}^{*} f(x|\theta_{i}^{*}))$, where $h_0$ is a known density function, while the deviated proportion $\lambda^{*}$ and latent mixing measure $G_{*} = \sum_{i = 1}^{k} p_{i}^{*} \delta_{\theta_i^{*}}$ associated with the mixture distribution are unknown. Via a novel notion of distinguishability between the known density $h_{0}$ and the deviated mixture distribution, we establish rates of convergence for the maximum likelihood estimates of $\lambda^{*}$ and $G^{*}$ under Wasserstein metric. Simulation studies are carried out to illustrate the theory.

Scalable nonparametric Bayesian learning for heterogeneous and dynamic velocity fields

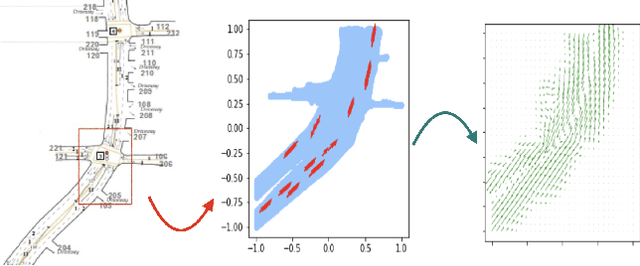
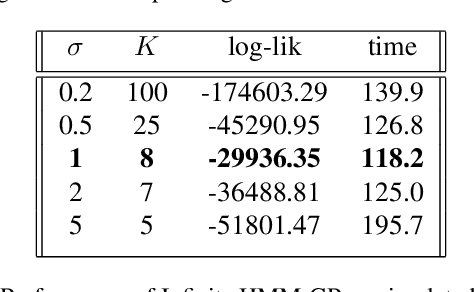
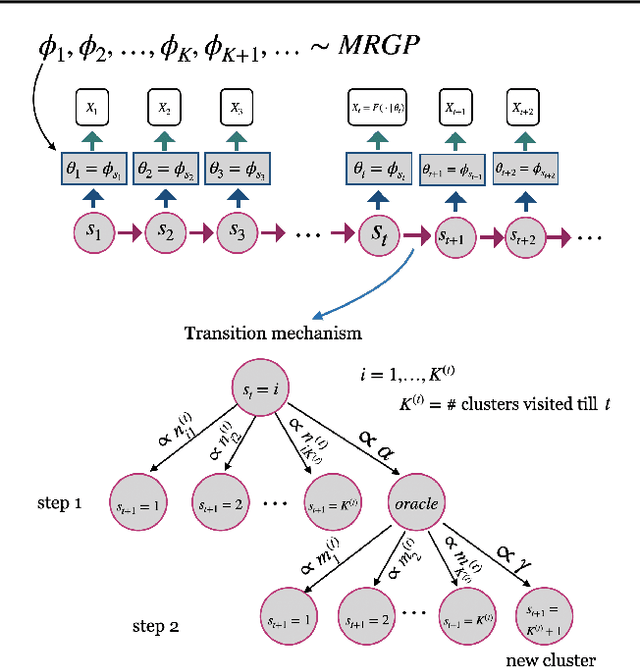
Analysis of heterogeneous patterns in complex spatio-temporal data finds usage across various domains in applied science and engineering, including training autonomous vehicles to navigate in complex traffic scenarios. Motivated by applications arising in the transportation domain, in this paper we develop a model for learning heterogeneous and dynamic patterns of velocity field data. We draw from basic nonparameric Bayesian modeling elements such as hierarchical Dirichlet process and infinite hidden Markov model, while the smoothness of each homogeneous velocity field element is captured with a Gaussian process prior. Of particular focus is a scalable approximate inference method for the proposed model; this is achieved by employing sequential MAP estimates from the infinite HMM model and an efficient sequential GP posterior computation technique, which is shown to work effectively on simulated data sets. Finally, we demonstrate the effectiveness of our techniques to the NGSIM dataset of complex multi-vehicle interactions.

Functional Optimal Transport: Mapping Estimation and Domain Adaptation for Functional data

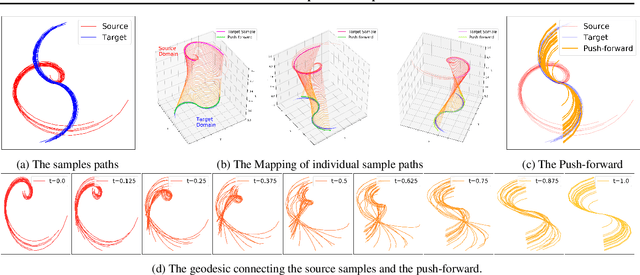
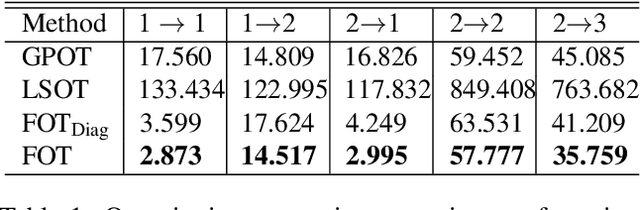
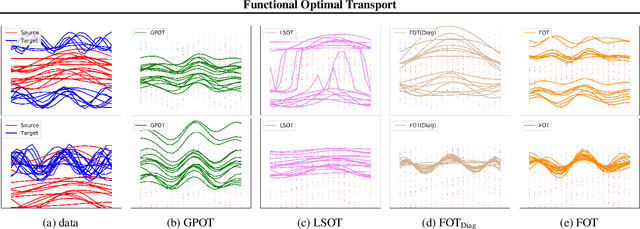
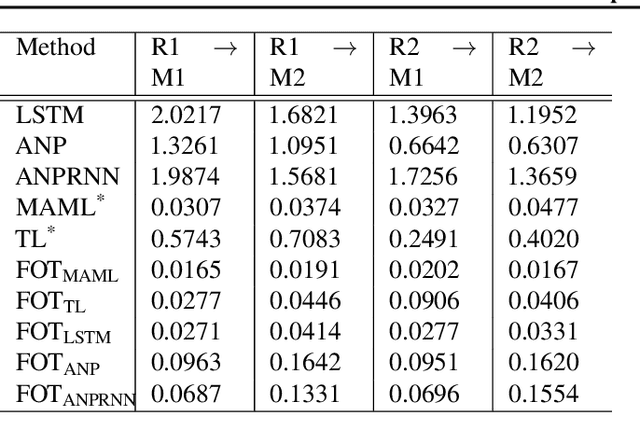
Optimal transport (OT) has generated much recent interest by its capability of finding mappings that transport mass from one distribution to another, and found useful roles in machine learning tasks such as unsupervised learning, domain adaptation and transfer learning. On the other hand, in many applications data are generated by complex mechanisms involving convoluted spaces of functions, curves and surfaces in high dimensions. Functional data analysis provides a useful framework of treatment for such domains. In this paper we introduce a novel formulation of optimal transport problem in functional spaces and develop an efficient learning algorithm for finding the stochastic map between functional domains. We apply our method to synthetic datasets and study the geometric properties of the transport map. Experiments on real-world datasets of robot arm trajectories and digit numbers further demonstrate the effectiveness of our method on applications of domain adaptation and generative modeling.

Robust Unsupervised Learning of Temporal Dynamic Interactions

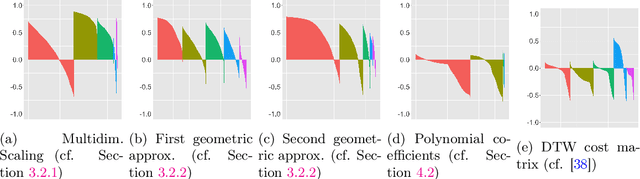
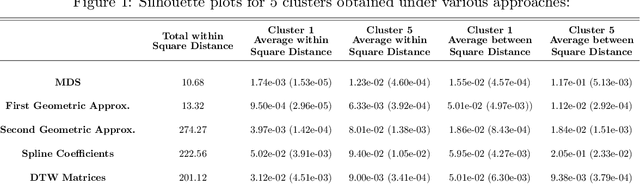
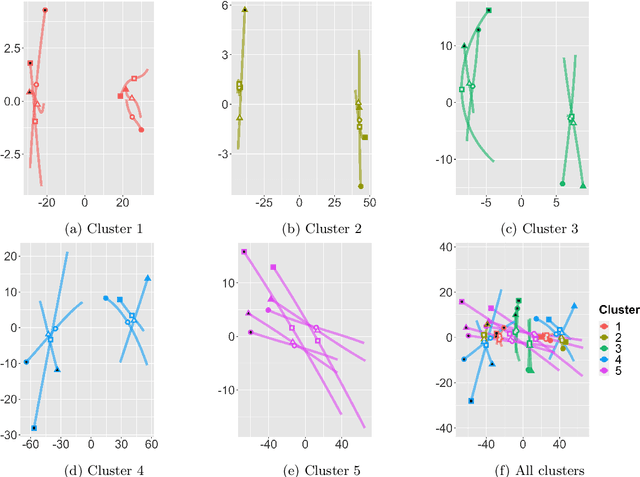
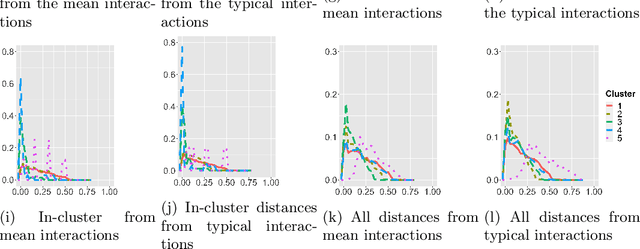
Robust representation learning of temporal dynamic interactions is an important problem in robotic learning in general and automated unsupervised learning in particular. Temporal dynamic interactions can be described by (multiple) geometric trajectories in a suitable space over which unsupervised learning techniques may be applied to extract useful features from raw and high-dimensional data measurements. Taking a geometric approach to robust representation learning for temporal dynamic interactions, it is necessary to develop suitable metrics and a systematic methodology for comparison and for assessing the stability of an unsupervised learning method with respect to its tuning parameters. Such metrics must account for the (geometric) constraints in the physical world as well as the uncertainty associated with the learned patterns. In this paper we introduce a model-free metric based on the Procrustes distance for robust representation learning of interactions, and an optimal transport based distance metric for comparing between distributions of interaction primitives. These distance metrics can serve as an objective for assessing the stability of an interaction learning algorithm. They are also used for comparing the outcomes produced by different algorithms. Moreover, they may also be adopted as an objective function to obtain clusters and representative interaction primitives. These concepts and techniques will be introduced, along with mathematical properties, while their usefulness will be demonstrated in unsupervised learning of vehicle-to-vechicle interactions extracted from the Safety Pilot database, the world's largest database for connected vehicles.

Rk-means: Fast Clustering for Relational Data

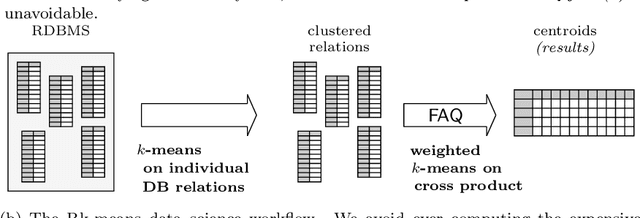
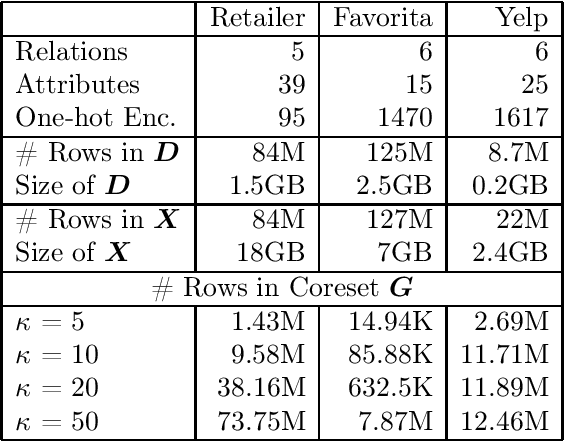
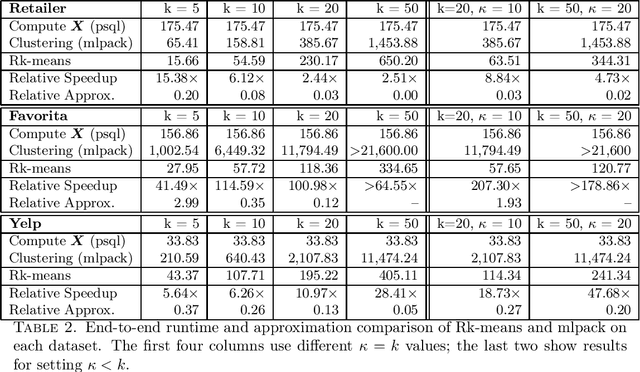
Conventional machine learning algorithms cannot be applied until a data matrix is available to process. When the data matrix needs to be obtained from a relational database via a feature extraction query, the computation cost can be prohibitive, as the data matrix may be (much) larger than the total input relation size. This paper introduces Rk-means, or relational k -means algorithm, for clustering relational data tuples without having to access the full data matrix. As such, we avoid having to run the expensive feature extraction query and storing its output. Our algorithm leverages the underlying structures in relational data. It involves construction of a small {\it grid coreset} of the data matrix for subsequent cluster construction. This gives a constant approximation for the k -means objective, while having asymptotic runtime improvements over standard approaches of first running the database query and then clustering. Empirical results show orders-of-magnitude speedup, and Rk-means can run faster on the database than even just computing the data matrix.

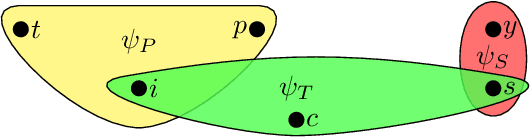
On Efficient Multilevel Clustering via Wasserstein Distances

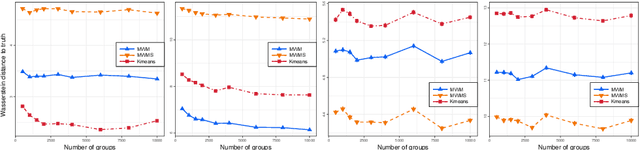
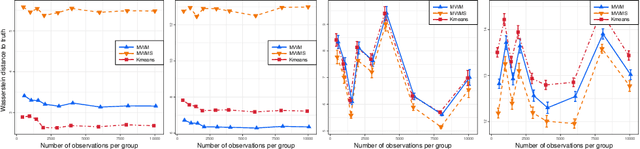
We propose a novel approach to the problem of multilevel clustering, which aims to simultaneously partition data in each group and discover grouping patterns among groups in a potentially large hierarchically structured corpus of data. Our method involves a joint optimization formulation over several spaces of discrete probability measures, which are endowed with Wasserstein distance metrics. We propose several variants of this problem, which admit fast optimization algorithms, by exploiting the connection to the problem of finding Wasserstein barycenters. Consistency properties are established for the estimates of both local and global clusters. Finally, the experimental results with both synthetic and real data are presented to demonstrate the flexibility and scalability of the proposed approach.

Dirichlet Simplex Nest and Geometric Inference

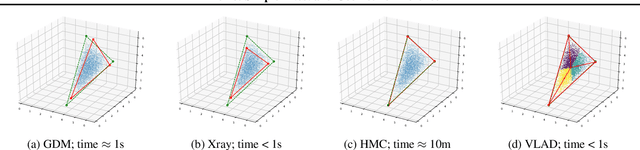
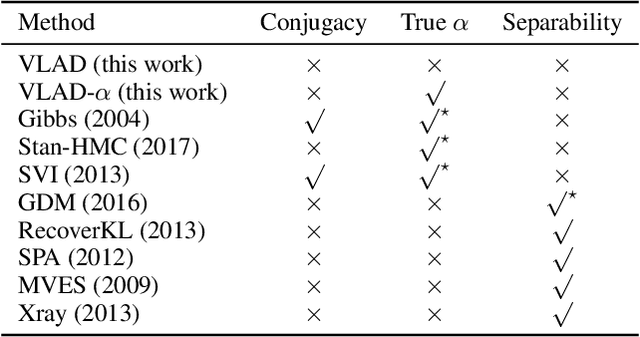
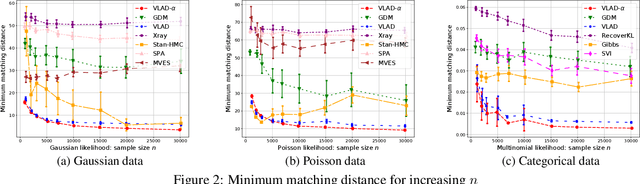
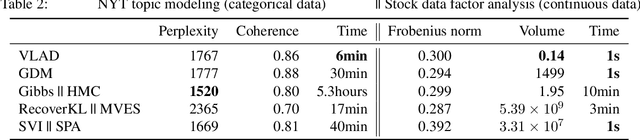
We propose Dirichlet Simplex Nest, a class of probabilistic models suitable for a variety of data types, and develop fast and provably accurate inference algorithms by accounting for the model's convex geometry and low dimensional simplicial structure. By exploiting the connection to Voronoi tessellation and properties of Dirichlet distribution, the proposed inference algorithm is shown to achieve consistency and strong error bound guarantees on a range of model settings and data distributions. The effectiveness of our model and the learning algorithm is demonstrated by simulations and by analyses of text and financial data.