Large Deviations for Sequential Tests of Statistical Sequence Matching

We revisit the problem of statistical sequence matching initiated by Unnikrishnan (TIT 2015) and derive theoretical performance guarantees for sequential tests that have bounded expected stopping times. Specifically, in this problem, one is given two databases of sequences and the task is to identify all matched pairs of sequences. In each database, each sequence is generated i.i.d. from a distinct distribution and a pair of sequences is said matched if they are generated from the same distribution. The generating distribution of each sequence is \emph{unknown}. We first consider the case where the number of matches is known and derive the exact exponential decay rate of the mismatch (error) probability, a.k.a. the mismatch exponent, under each hypothesis for optimal sequential tests. Our results reveal the benefit of sequentiality by showing that optimal sequential tests have larger mismatch exponent than fixed-length tests by Zhou \emph{et al.} (TIT 2024). Subsequently, we generalize our achievability result to the case of unknown number of matches. In this case, two additional error probabilities arise: false alarm and false reject probabilities. We propose a corresponding sequential test, show that the test has bounded expected stopping time under certain conditions, and characterize the tradeoff among the exponential decay rates of three error probabilities. Furthermore, we reveal the benefit of sequentiality over the two-step fixed-length test by Zhou \emph{et al.} (TIT 2024) and propose an one-step fixed-length test that has no worse performance than the fixed-length test by Zhou \emph{et al.} (TIT 2024). When specialized to the case where either database contains a single sequence, our results specialize to large deviations of sequential tests for statistical classification, the binary case of which was recently studied by Hsu, Li and Wang (ITW 2022).

Asymptotics for Outlier Hypothesis Testing

We revisit the outlier hypothesis testing framework of Li \emph{et al.} (TIT 2014) and derive fundamental limits for the optimal test. In outlier hypothesis testing, one is given multiple observed sequences, where most sequences are generated i.i.d. from a nominal distribution. The task is to discern the set of outlying sequences that are generated according to anomalous distributions. The nominal and anomalous distributions are \emph{unknown}. We consider the case of multiple outliers where the number of outliers is unknown and each outlier can follow a different anomalous distribution. Under this setting, we study the tradeoff among the probabilities of misclassification error, false alarm and false reject. Specifically, we propose a threshold-based test that ensures exponential decay of misclassification error and false alarm probabilities. We study two constraints on the false reject probability, with one constraint being that it is a non-vanishing constant and the other being that it has an exponential decay rate. For both cases, we characterize bounds on the false reject probability, as a function of the threshold, for each tuple of nominal and anomalous distributions. Finally, we demonstrate the asymptotic optimality of our test under the generalized Neyman-Pearson criterion.

Learning Geo-Temporal Non-Stationary Failure and Recovery of Power Distribution

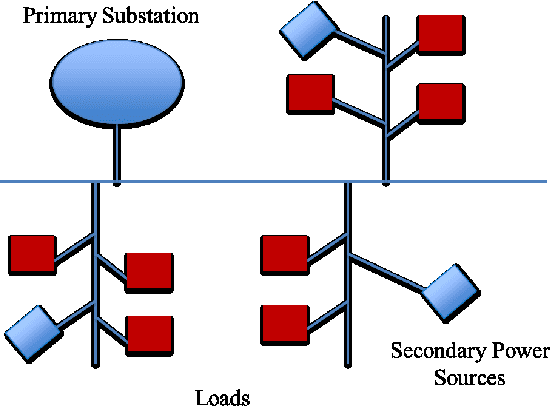
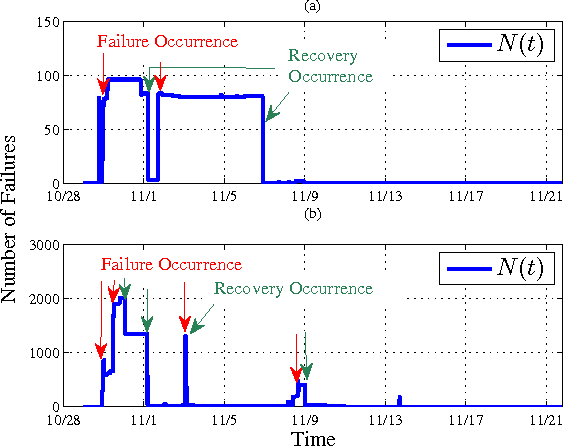
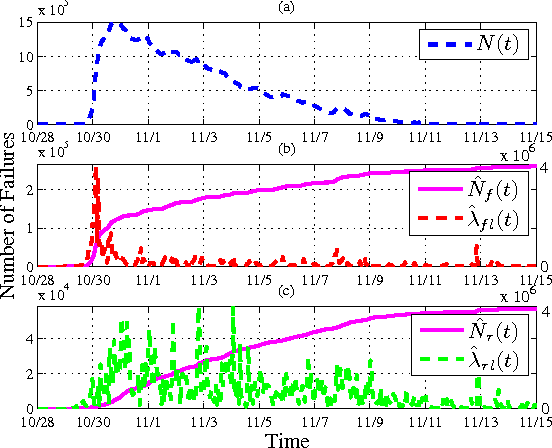
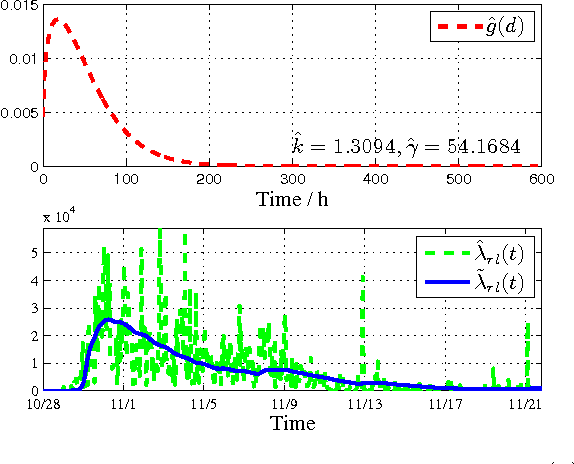
Smart energy grid is an emerging area for new applications of machine learning in a non-stationary environment. Such a non-stationary environment emerges when large-scale failures occur at power distribution networks due to external disturbances such as hurricanes and severe storms. Power distribution networks lie at the edge of the grid, and are especially vulnerable to external disruptions. Quantifiable approaches are lacking and needed to learn non-stationary behaviors of large-scale failure and recovery of power distribution. This work studies such non-stationary behaviors in three aspects. First, a novel formulation is derived for an entire life cycle of large-scale failure and recovery of power distribution. Second, spatial-temporal models of failure and recovery of power distribution are developed as geo-location based multivariate non-stationary GI(t)/G(t)/Infinity queues. Third, the non-stationary spatial-temporal models identify a small number of parameters to be learned. Learning is applied to two real-life examples of large-scale disruptions. One is from Hurricane Ike, where data from an operational network is exact on failures and recoveries. The other is from Hurricane Sandy, where aggregated data is used for inferring failure and recovery processes at one of the impacted areas. Model parameters are learned using real data. Two findings emerge as results of learning: (a) Failure rates behave similarly at the two different provider networks for two different hurricanes but differently at the geographical regions. (b) Both rapid- and slow-recovery are present for Hurricane Ike but only slow recovery is shown for a regional distribution network from Hurricane Sandy.