QirK: Question Answering via Intermediate Representation on Knowledge Graphs

We demonstrate QirK, a system for answering natural language questions on Knowledge Graphs (KG). QirK can answer structurally complex questions that are still beyond the reach of emerging Large Language Models (LLMs). It does so using a unique combination of database technology, LLMs, and semantic search over vector embeddings. The glue for these components is an intermediate representation (IR). The input question is mapped to IR using LLMs, which is then repaired into a valid relational database query with the aid of a semantic search on vector embeddings. This allows a practical synthesis of LLM capabilities and KG reliability. A short video demonstrating QirK is available at https://youtu.be/6c81BLmOZ0U.

CHORUS: Foundation Models for Unified Data Discovery and Exploration

We explore the application of foundation models to data discovery and exploration tasks. Foundation models are large language models (LLMs) that show promising performance on a range of diverse tasks unrelated to their training. We show that these models are highly applicable to the data discovery and data exploration domain. When carefully used, they have superior capability on three representative tasks: table-class detection, column-type annotation and join-column prediction. On all three tasks, we show that a foundation-model-based approach outperforms the task-specific models and so the state of the art. Further, our approach often surpasses human-expert task performance. This suggests a future direction in which disparate data management tasks can be unified under foundation models.

Functional Collection Programming with Semi-Ring Dictionaries

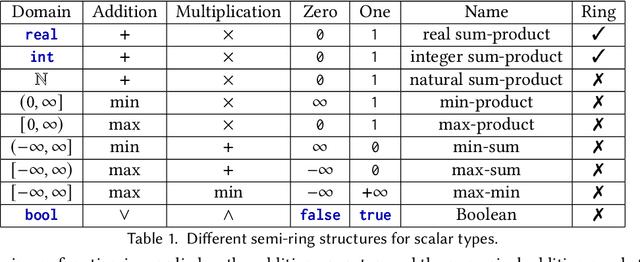
This paper introduces semi-ring dictionaries, a powerful class of compositional and purely functional collections that subsume other collection types such as sets, multisets, arrays, vectors, and matrices. We develop SDQL, a statically typed language centered around semi-ring dictionaries, that can encode expressions in relational algebra with aggregations, functional collections, and linear algebra. Furthermore, thanks to the semi-ring algebraic structures behind these dictionaries, SDQL unifies a wide range of optimizations commonly used in databases and linear algebra. As a result, SDQL enables efficient processing of hybrid database and linear algebra workloads, by putting together optimizations that are otherwise confined to either database systems or linear algebra frameworks. Through experimental results, we show that a handful of relational and linear algebra workloads can take advantage of the SDQL language and optimizations. Overall, we observe that SDQL achieves competitive performance to Typer and Tectorwise, which are state-of-the-art in-memory systems for (flat, not nested) relational data, and achieves an average 2x speedup over SciPy for linear algebra workloads. Finally, for hybrid workloads involving linear algebra processing over nested biomedical data, SDQL can give up to one order of magnitude speedup over Trance, a state-of-the-art nested relational engine.

The Relational Data Borg is Learning

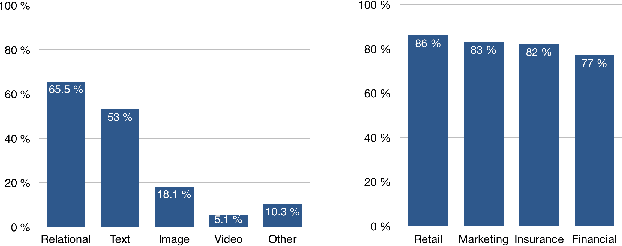
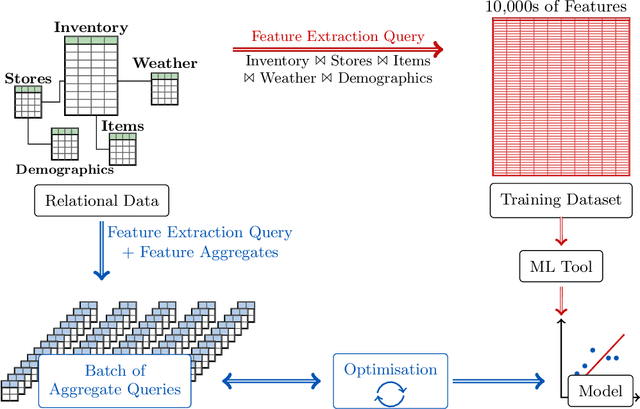
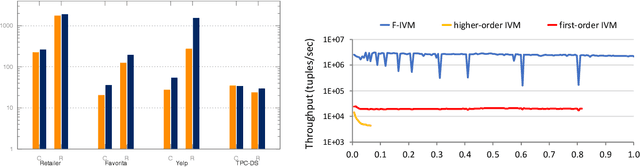
This paper overviews an approach that addresses machine learning over relational data as a database problem. This is justified by two observations. First, the input to the learning task is commonly the result of a feature extraction query over the relational data. Second, the learning task requires the computation of group-by aggregates. This approach has been already investigated for a number of supervised and unsupervised learning tasks, including: ridge linear regression, factorisation machines, support vector machines, decision trees, principal component analysis, and k-means; and also for linear algebra over data matrices. The main message of this work is that the runtime performance of machine learning can be dramatically boosted by a toolbox of techniques that exploit the knowledge of the underlying data. This includes theoretical development on the algebraic, combinatorial, and statistical structure of relational data processing and systems development on code specialisation, low-level computation sharing, and parallelisation. These techniques aim at lowering both the complexity and the constant factors of the learning time. This work is the outcome of extensive collaboration of the author with colleagues from RelationalAI, in particular Mahmoud Abo Khamis, Molham Aref, Hung Ngo, and XuanLong Nguyen, and from the FDB research project, in particular Ahmet Kara, Milos Nikolic, Maximilian Schleich, Amir Shaikhha, Jakub Zavodny, and Haozhe Zhang. The author would also like to thank the members of the FDB project for the figures and examples used in this paper. The author is grateful for support from industry: Amazon Web Services, Google, Infor, LogicBlox, Microsoft Azure, RelationalAI; and from the funding agencies EPSRC and ERC. This project has received funding from the European Union's Horizon 2020 research and innovation programme under grant agreement No 682588.

Multi-layer Optimizations for End-to-End Data Analytics

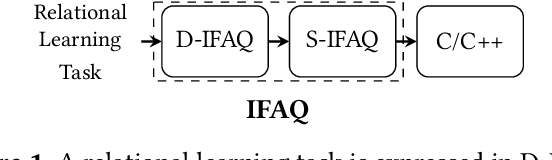
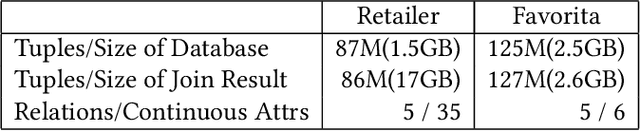
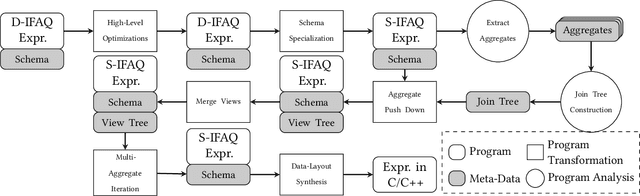
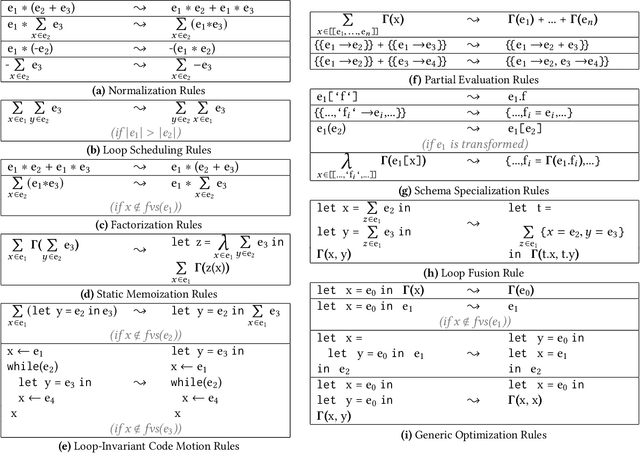
We consider the problem of training machine learning models over multi-relational data. The mainstream approach is to first construct the training dataset using a feature extraction query over input database and then use a statistical software package of choice to train the model. In this paper we introduce Iterative Functional Aggregate Queries (IFAQ), a framework that realizes an alternative approach. IFAQ treats the feature extraction query and the learning task as one program given in the IFAQ's domain-specific language, which captures a subset of Python commonly used in Jupyter notebooks for rapid prototyping of machine learning applications. The program is subject to several layers of IFAQ optimizations, such as algebraic transformations, loop transformations, schema specialization, data layout optimizations, and finally compilation into efficient low-level C++ code specialized for the given workload and data. We show that a Scala implementation of IFAQ can outperform mlpack, Scikit, and TensorFlow by several orders of magnitude for linear regression and regression tree models over several relational datasets.

Rk-means: Fast Clustering for Relational Data

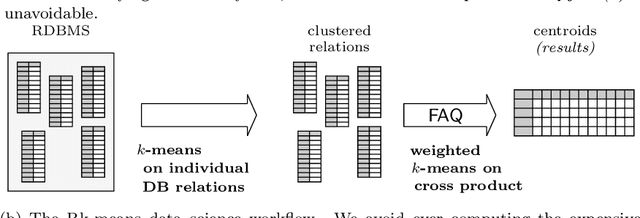
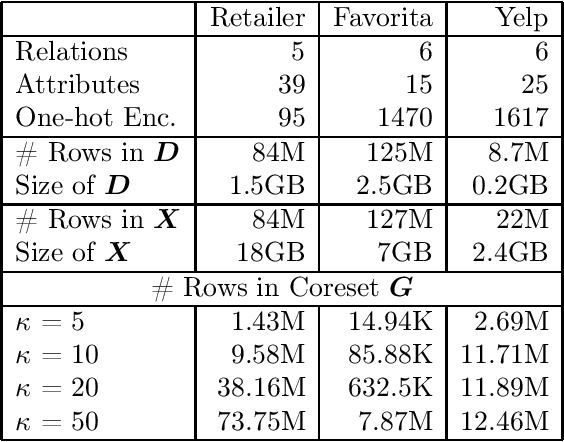
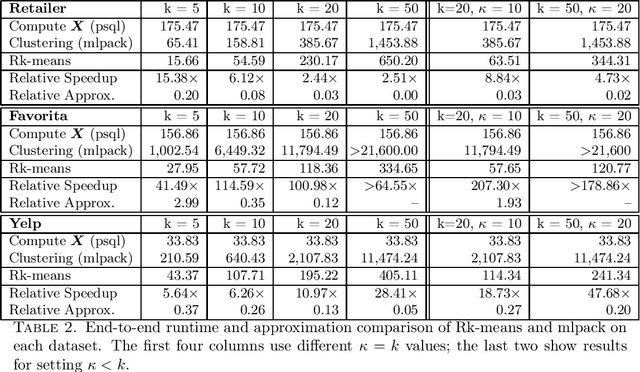
Conventional machine learning algorithms cannot be applied until a data matrix is available to process. When the data matrix needs to be obtained from a relational database via a feature extraction query, the computation cost can be prohibitive, as the data matrix may be (much) larger than the total input relation size. This paper introduces Rk-means, or relational k -means algorithm, for clustering relational data tuples without having to access the full data matrix. As such, we avoid having to run the expensive feature extraction query and storing its output. Our algorithm leverages the underlying structures in relational data. It involves construction of a small {\it grid coreset} of the data matrix for subsequent cluster construction. This gives a constant approximation for the k -means objective, while having asymptotic runtime improvements over standard approaches of first running the database query and then clustering. Empirical results show orders-of-magnitude speedup, and Rk-means can run faster on the database than even just computing the data matrix.

On Functional Aggregate Queries with Additive Inequalities

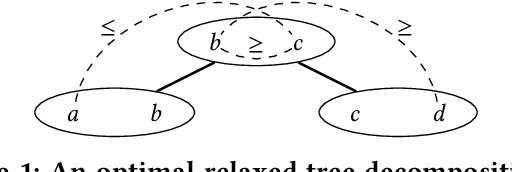
Motivated by fundamental applications in databases and relational machine learning, we formulate and study the problem of answering Functional Aggregate Queries (FAQ) in which some of the input factors are defined by a collection of Additive Inequalities between variables. We refer to these queries as FAQ-AI for short. To answer FAQ-AI in the Boolean semiring, we define "relaxed" tree decompositions and "relaxed" submodular and fractional hypertree width parameters. We show that an extension of the InsideOut algorithm using Chazelle's geometric data structure for solving the semigroup range search problem can answer Boolean FAQ-AI in time given by these new width parameters. This new algorithm achieves lower complexity than known solutions for FAQ-AI. It also recovers some known results in database query answering. Our second contribution is a relaxation of the set of polymatroids that gives rise to the counting version of the submodular width, denoted by "#subw". This new width is sandwiched between the submodular and the fractional hypertree widths. Any FAQ and FAQ-AI over one semiring can be answered in time proportional to #subw and respectively to the relaxed version of #subw. We present three applications of our FAQ-AI framework to relational machine learning: k-means clustering, training linear support vector machines, and training models using non-polynomial loss. These optimization problems can be solved over a database asymptotically faster than computing the join of the database relations.

Declarative Statistical Modeling with Datalog

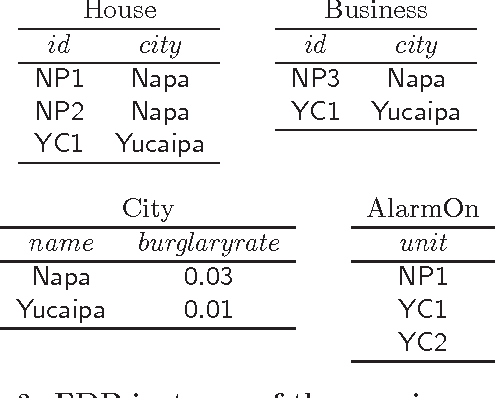
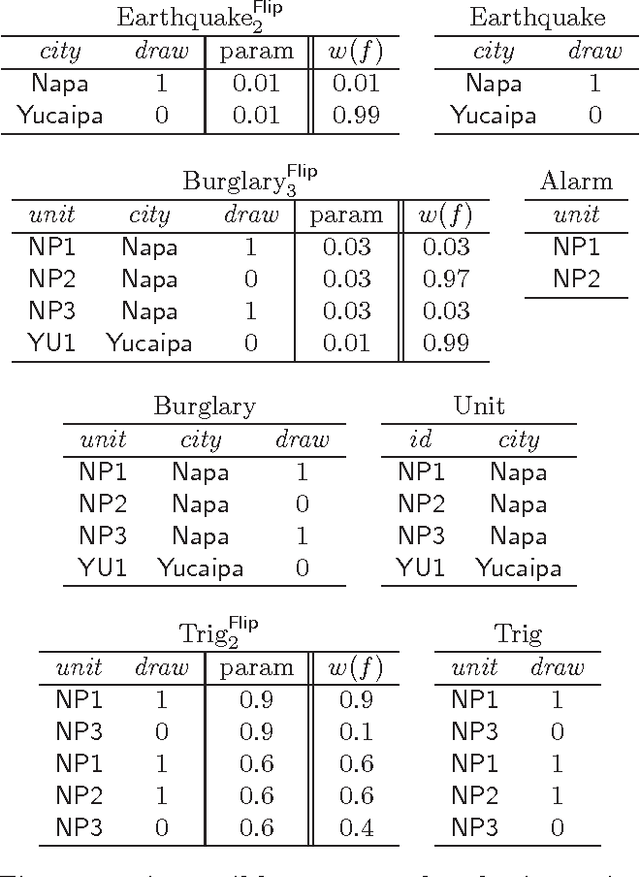
Formalisms for specifying statistical models, such as probabilistic-programming languages, typically consist of two components: a specification of a stochastic process (the prior), and a specification of observations that restrict the probability space to a conditional subspace (the posterior). Use cases of such formalisms include the development of algorithms in machine learning and artificial intelligence. We propose and investigate a declarative framework for specifying statistical models on top of a database, through an appropriate extension of Datalog. By virtue of extending Datalog, our framework offers a natural integration with the database, and has a robust declarative semantics. Our Datalog extension provides convenient mechanisms to include numerical probability functions; in particular, conclusions of rules may contain values drawn from such functions. The semantics of a program is a probability distribution over the possible outcomes of the input database with respect to the program; these outcomes are minimal solutions with respect to a related program with existentially quantified variables in conclusions. Observations are naturally incorporated by means of integrity constraints over the extensional and intensional relations. We focus on programs that use discrete numerical distributions, but even then the space of possible outcomes may be uncountable (as a solution can be infinite). We define a probability measure over possible outcomes by applying the known concept of cylinder sets to a probabilistic chase procedure. We show that the resulting semantics is robust under different chases. We also identify conditions guaranteeing that all possible outcomes are finite (and then the probability space is discrete). We argue that the framework we propose retains the purely declarative nature of Datalog, and allows for natural specifications of statistical models.

Conditioning Probabilistic Databases

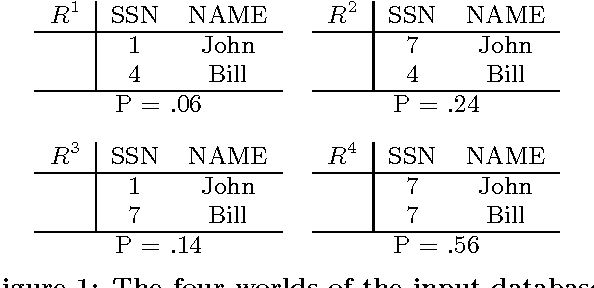
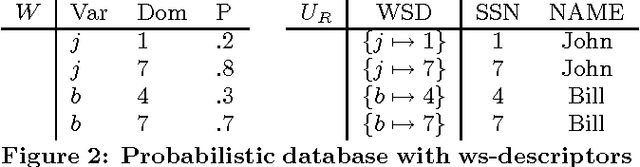
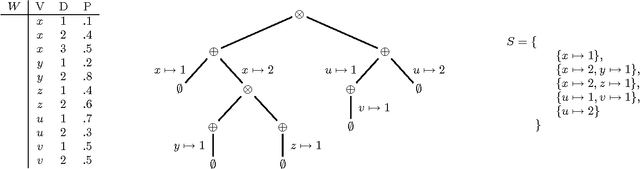
Past research on probabilistic databases has studied the problem of answering queries on a static database. Application scenarios of probabilistic databases however often involve the conditioning of a database using additional information in the form of new evidence. The conditioning problem is thus to transform a probabilistic database of priors into a posterior probabilistic database which is materialized for subsequent query processing or further refinement. It turns out that the conditioning problem is closely related to the problem of computing exact tuple confidence values. It is known that exact confidence computation is an NP-hard problem. This has led researchers to consider approximation techniques for confidence computation. However, neither conditioning nor exact confidence computation can be solved using such techniques. In this paper we present efficient techniques for both problems. We study several problem decomposition methods and heuristics that are based on the most successful search techniques from constraint satisfaction, such as the Davis-Putnam algorithm. We complement this with a thorough experimental evaluation of the algorithms proposed. Our experiments show that our exact algorithms scale well to realistic database sizes and can in some scenarios compete with the most efficient previous approximation algorithms.