Wotao Yin
Communication-Efficient Topologies for Decentralized Learning with $O(1)$ Consensus Rate
Oct 14, 2022
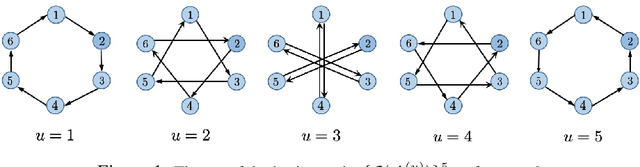
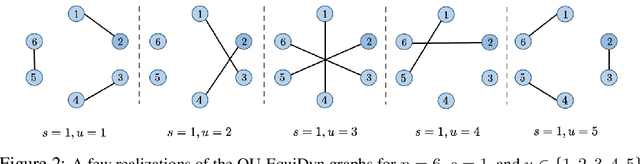

Abstract:Decentralized optimization is an emerging paradigm in distributed learning in which agents achieve network-wide solutions by peer-to-peer communication without the central server. Since communication tends to be slower than computation, when each agent communicates with only a few neighboring agents per iteration, they can complete iterations faster than with more agents or a central server. However, the total number of iterations to reach a network-wide solution is affected by the speed at which the agents' information is ``mixed'' by communication. We found that popular communication topologies either have large maximum degrees (such as stars and complete graphs) or are ineffective at mixing information (such as rings and grids). To address this problem, we propose a new family of topologies, EquiTopo, which has an (almost) constant degree and a network-size-independent consensus rate that is used to measure the mixing efficiency. In the proposed family, EquiStatic has a degree of $\Theta(\ln(n))$, where $n$ is the network size, and a series of time-dependent one-peer topologies, EquiDyn, has a constant degree of 1. We generate EquiDyn through a certain random sampling procedure. Both of them achieve an $n$-independent consensus rate. We apply them to decentralized SGD and decentralized gradient tracking and obtain faster communication and better convergence, theoretically and empirically. Our code is implemented through BlueFog and available at \url{https://github.com/kexinjinnn/EquiTopo}
On Representing Linear Programs by Graph Neural Networks
Sep 25, 2022
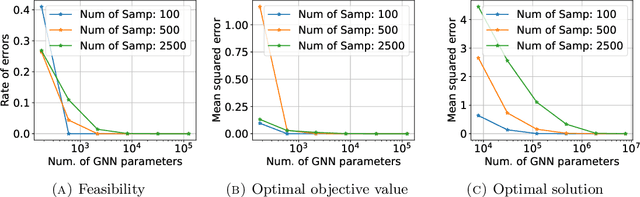
Abstract:Learning to optimize is a rapidly growing area that aims to solve optimization problems or improve existing optimization algorithms using machine learning (ML). In particular, the graph neural network (GNN) is considered a suitable ML model for optimization problems whose variables and constraints are permutation--invariant, for example, the linear program (LP). While the literature has reported encouraging numerical results, this paper establishes the theoretical foundation of applying GNNs to solving LPs. Given any size limit of LPs, we construct a GNN that maps different LPs to different outputs. We show that properly built GNNs can reliably predict feasibility, boundedness, and an optimal solution for each LP in a broad class. Our proofs are based upon the recently--discovered connections between the Weisfeiler--Lehman isomorphism test and the GNN. To validate our results, we train a simple GNN and present its accuracy in mapping LPs to their feasibilities and solutions.
Lower Bounds and Nearly Optimal Algorithms in Distributed Learning with Communication Compression
Jun 08, 2022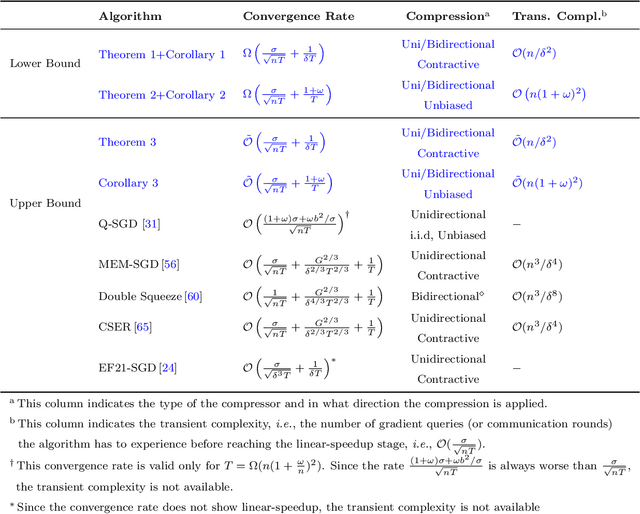
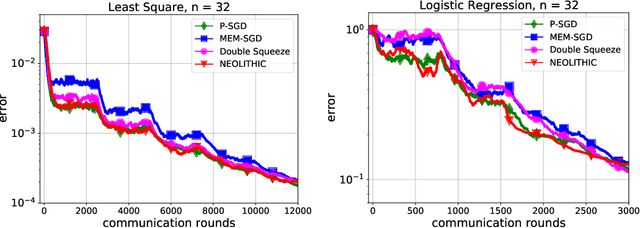
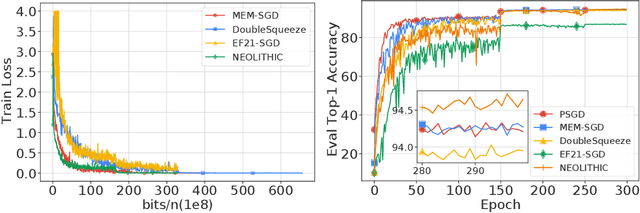
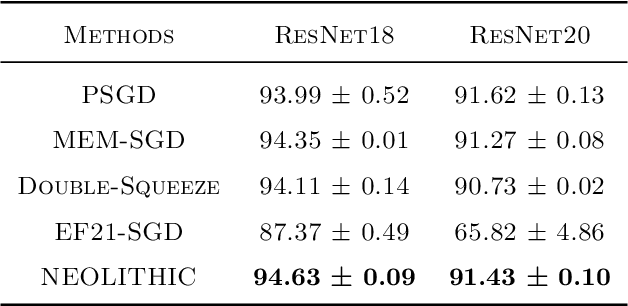
Abstract:Recent advances in distributed optimization and learning have shown that communication compression is one of the most effective means of reducing communication. While there have been many results on convergence rates under communication compression, a theoretical lower bound is still missing. Analyses of algorithms with communication compression have attributed convergence to two abstract properties: the unbiased property or the contractive property. They can be applied with either unidirectional compression (only messages from workers to server are compressed) or bidirectional compression. In this paper, we consider distributed stochastic algorithms for minimizing smooth and non-convex objective functions under communication compression. We establish a convergence lower bound for algorithms whether using unbiased or contractive compressors in unidirection or bidirection. To close the gap between the lower bound and the existing upper bounds, we further propose an algorithm, NEOLITHIC, which almost reaches our lower bound (up to logarithm factors) under mild conditions. Our results also show that using contractive bidirectional compression can yield iterative methods that converge as fast as those using unbiased unidirectional compression. The experimental results validate our findings.
FiLM: Frequency improved Legendre Memory Model for Long-term Time Series Forecasting
May 24, 2022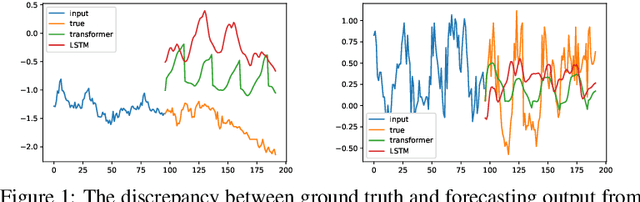
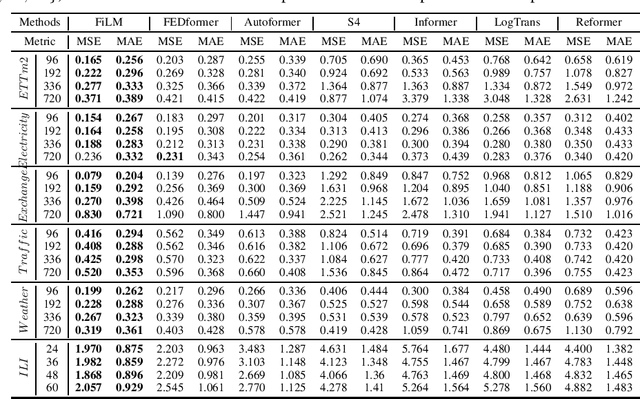
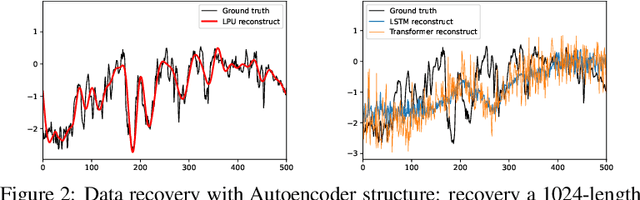
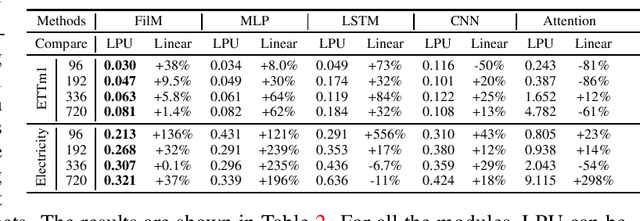
Abstract:Recent studies have shown that deep learning models such as RNNs and Transformers have brought significant performance gains for long-term forecasting of time series because they effectively utilize historical information. We found, however, that there is still great room for improvement in how to preserve historical information in neural networks while avoiding overfitting to noise presented in the history. Addressing this allows better utilization of the capabilities of deep learning models. To this end, we design a \textbf{F}requency \textbf{i}mproved \textbf{L}egendre \textbf{M}emory model, or {\bf FiLM}: it applies Legendre Polynomials projections to approximate historical information, uses Fourier projection to remove noise, and adds a low-rank approximation to speed up computation. Our empirical studies show that the proposed FiLM significantly improves the accuracy of state-of-the-art models in multivariate and univariate long-term forecasting by (\textbf{20.3\%}, \textbf{22.6\%}), respectively. We also demonstrate that the representation module developed in this work can be used as a general plug-in to improve the long-term prediction performance of other deep learning modules. Code will be released soon.
A Novel Convergence Analysis for Algorithms of the Adam Family
Dec 07, 2021

Abstract:Since its invention in 2014, the Adam optimizer has received tremendous attention. On one hand, it has been widely used in deep learning and many variants have been proposed, while on the other hand their theoretical convergence property remains to be a mystery. It is far from satisfactory in the sense that some studies require strong assumptions about the updates, which are not necessarily applicable in practice, while other studies still follow the original problematic convergence analysis of Adam, which was shown to be not sufficient to ensure convergence. Although rigorous convergence analysis exists for Adam, they impose specific requirements on the update of the adaptive step size, which are not generic enough to cover many other variants of Adam. To address theses issues, in this extended abstract, we present a simple and generic proof of convergence for a family of Adam-style methods (including Adam, AMSGrad, Adabound, etc.). Our analysis only requires an increasing or large "momentum" parameter for the first-order moment, which is indeed the case used in practice, and a boundness condition on the adaptive factor of the step size, which applies to all variants of Adam under mild conditions of stochastic gradients. We also establish a variance diminishing result for the used stochastic gradient estimators. Indeed, our analysis of Adam is so simple and generic that it can be leveraged to establish the convergence for solving a broader family of non-convex optimization problems, including min-max, compositional, and bilevel optimization problems. For the full (earlier) version of this extended abstract, please refer to arXiv:2104.14840.
BlueFog: Make Decentralized Algorithms Practical for Optimization and Deep Learning
Nov 08, 2021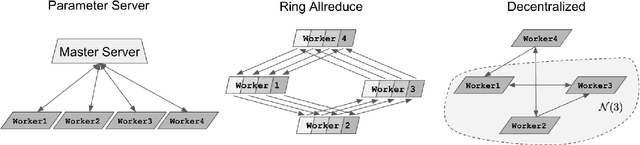
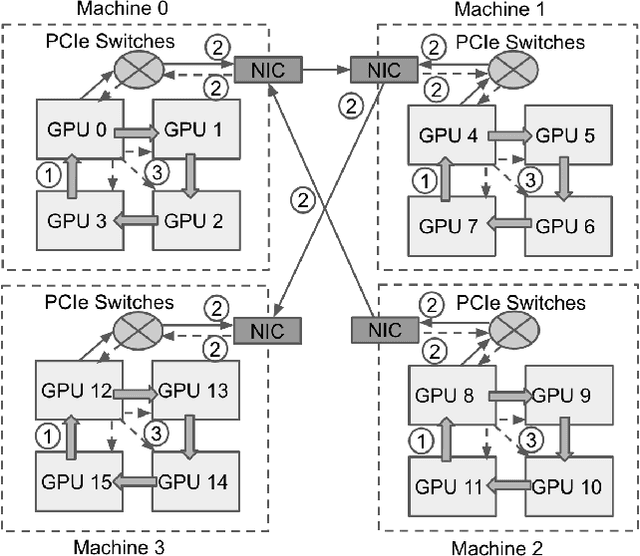
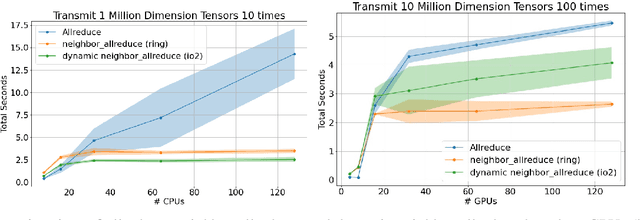
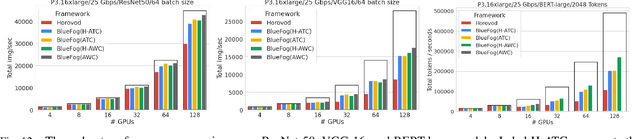
Abstract:Decentralized algorithm is a form of computation that achieves a global goal through local dynamics that relies on low-cost communication between directly-connected agents. On large-scale optimization tasks involving distributed datasets, decentralized algorithms have shown strong, sometimes superior, performance over distributed algorithms with a central node. Recently, developing decentralized algorithms for deep learning has attracted great attention. They are considered as low-communication-overhead alternatives to those using a parameter server or the Ring-Allreduce protocol. However, the lack of an easy-to-use and efficient software package has kept most decentralized algorithms merely on paper. To fill the gap, we introduce BlueFog, a python library for straightforward, high-performance implementations of diverse decentralized algorithms. Based on a unified abstraction of various communication operations, BlueFog offers intuitive interfaces to implement a spectrum of decentralized algorithms, from those using a static, undirected graph for synchronous operations to those using dynamic and directed graphs for asynchronous operations. BlueFog also adopts several system-level acceleration techniques to further optimize the performance on the deep learning tasks. On mainstream DNN training tasks, BlueFog reaches a much higher throughput and achieves an overall $1.2\times \sim 1.8\times$ speedup over Horovod, a state-of-the-art distributed deep learning package based on Ring-Allreduce. BlueFog is open source at https://github.com/Bluefog-Lib/bluefog.
Hyperparameter Tuning is All You Need for LISTA
Oct 29, 2021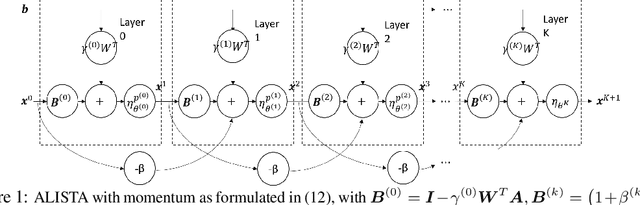
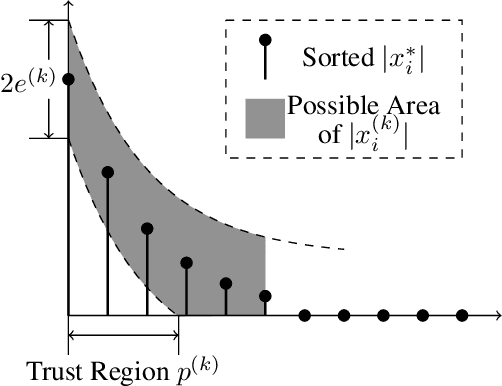
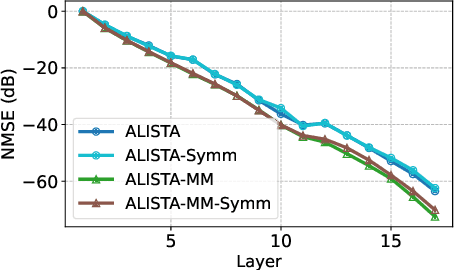
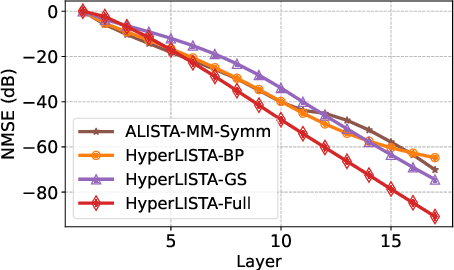
Abstract:Learned Iterative Shrinkage-Thresholding Algorithm (LISTA) introduces the concept of unrolling an iterative algorithm and training it like a neural network. It has had great success on sparse recovery. In this paper, we show that adding momentum to intermediate variables in the LISTA network achieves a better convergence rate and, in particular, the network with instance-optimal parameters is superlinearly convergent. Moreover, our new theoretical results lead to a practical approach of automatically and adaptively calculating the parameters of a LISTA network layer based on its previous layers. Perhaps most surprisingly, such an adaptive-parameter procedure reduces the training of LISTA to tuning only three hyperparameters from data: a new record set in the context of the recent advances on trimming down LISTA complexity. We call this new ultra-light weight network HyperLISTA. Compared to state-of-the-art LISTA models, HyperLISTA achieves almost the same performance on seen data distributions and performs better when tested on unseen distributions (specifically, those with different sparsity levels and nonzero magnitudes). Code is available: https://github.com/VITA-Group/HyperLISTA.
Exponential Graph is Provably Efficient for Decentralized Deep Training
Oct 26, 2021
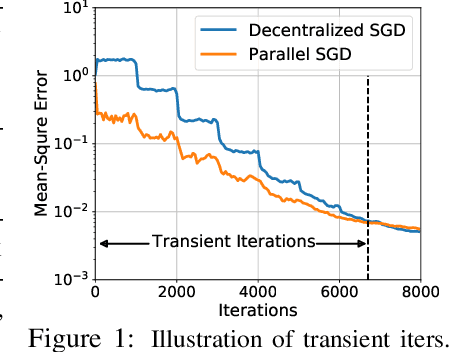
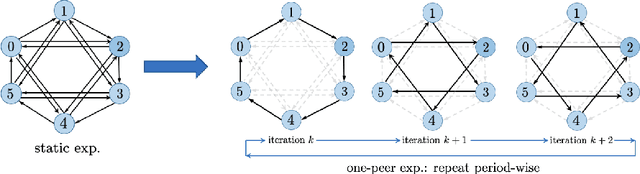
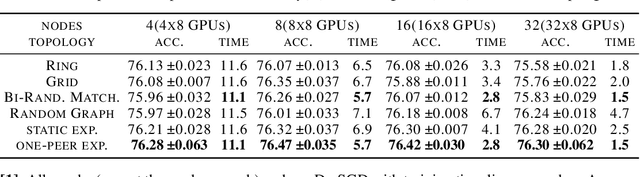
Abstract:Decentralized SGD is an emerging training method for deep learning known for its much less (thus faster) communication per iteration, which relaxes the averaging step in parallel SGD to inexact averaging. The less exact the averaging is, however, the more the total iterations the training needs to take. Therefore, the key to making decentralized SGD efficient is to realize nearly-exact averaging using little communication. This requires a skillful choice of communication topology, which is an under-studied topic in decentralized optimization. In this paper, we study so-called exponential graphs where every node is connected to $O(\log(n))$ neighbors and $n$ is the total number of nodes. This work proves such graphs can lead to both fast communication and effective averaging simultaneously. We also discover that a sequence of $\log(n)$ one-peer exponential graphs, in which each node communicates to one single neighbor per iteration, can together achieve exact averaging. This favorable property enables one-peer exponential graph to average as effective as its static counterpart but communicates more efficiently. We apply these exponential graphs in decentralized (momentum) SGD to obtain the state-of-the-art balance between per-iteration communication and iteration complexity among all commonly-used topologies. Experimental results on a variety of tasks and models demonstrate that decentralized (momentum) SGD over exponential graphs promises both fast and high-quality training. Our code is implemented through BlueFog and available at https://github.com/Bluefog-Lib/NeurIPS2021-Exponential-Graph.
Learned Robust PCA: A Scalable Deep Unfolding Approach for High-Dimensional Outlier Detection
Oct 11, 2021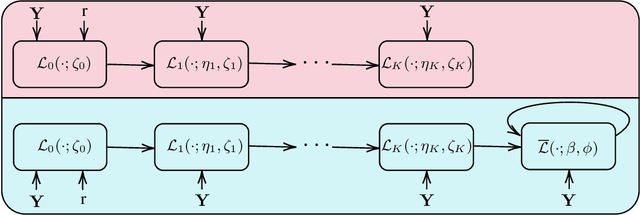

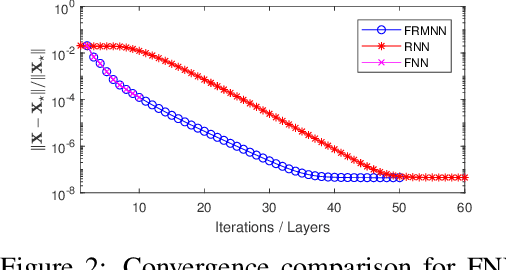
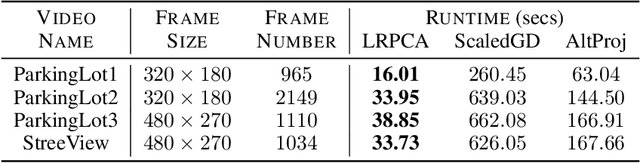
Abstract:Robust principal component analysis (RPCA) is a critical tool in modern machine learning, which detects outliers in the task of low-rank matrix reconstruction. In this paper, we propose a scalable and learnable non-convex approach for high-dimensional RPCA problems, which we call Learned Robust PCA (LRPCA). LRPCA is highly efficient, and its free parameters can be effectively learned to optimize via deep unfolding. Moreover, we extend deep unfolding from finite iterations to infinite iterations via a novel feedforward-recurrent-mixed neural network model. We establish the recovery guarantee of LRPCA under mild assumptions for RPCA. Numerical experiments show that LRPCA outperforms the state-of-the-art RPCA algorithms, such as ScaledGD and AltProj, on both synthetic datasets and real-world applications.
Curvature-Aware Derivative-Free Optimization
Sep 27, 2021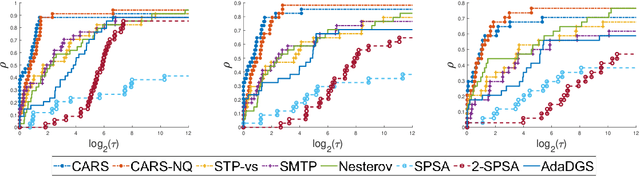
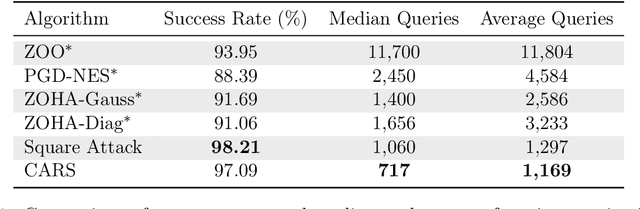
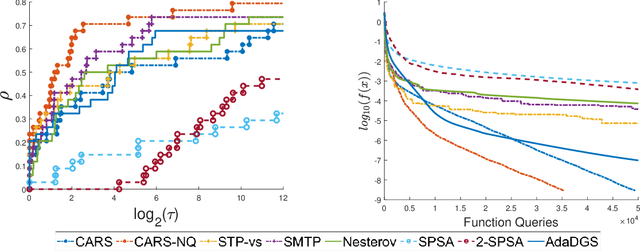

Abstract:We propose a new line-search method, coined Curvature-Aware Random Search (CARS), for derivative-free optimization. CARS exploits approximate curvature information to estimate the optimal step-size given a search direction. We prove that for strongly convex objective functions, CARS converges linearly if the search direction is drawn from a distribution satisfying very mild conditions. We also explore a variant, CARS-NQ, which uses Numerical Quadrature instead of a Monte Carlo method when approximating curvature along the search direction. We show CARS-NQ is effective on highly non-convex problems of the form $f = f_{\mathrm{cvx}} + f_{\mathrm{osc}}$ where $f_{\mathrm{cvx}}$ is strongly convex and $f_{\mathrm{osc}}$ is rapidly oscillating. Experimental results show that CARS and CARS-NQ match or exceed the state-of-the-arts on benchmark problem sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge