A Disentangled Low-Rank RNN Framework for Uncovering Neural Connectivity and Dynamics

Low-rank recurrent neural networks (lrRNNs) are a class of models that uncover low-dimensional latent dynamics underlying neural population activity. Although their functional connectivity is low-rank, it lacks disentanglement interpretations, making it difficult to assign distinct computational roles to different latent dimensions. To address this, we propose the Disentangled Recurrent Neural Network (DisRNN), a generative lrRNN framework that assumes group-wise independence among latent dynamics while allowing flexible within-group entanglement. These independent latent groups allow latent dynamics to evolve separately, but are internally rich for complex computation. We reformulate the lrRNN under a variational autoencoder (VAE) framework, enabling us to introduce a partial correlation penalty that encourages disentanglement between groups of latent dimensions. Experiments on synthetic, monkey M1, and mouse voltage imaging data show that DisRNN consistently improves the disentanglement and interpretability of learned neural latent trajectories in low-dimensional space and low-rank connectivity over baseline lrRNNs that do not encourage partial disentanglement.

Uncovering Semantic Selectivity of Latent Groups in Higher Visual Cortex with Mutual Information-Guided Diffusion

Understanding how neural populations in higher visual areas encode object-centered visual information remains a central challenge in computational neuroscience. Prior works have investigated representational alignment between artificial neural networks and the visual cortex. Nevertheless, these findings are indirect and offer limited insights to the structure of neural populations themselves. Similarly, decoding-based methods have quantified semantic features from neural populations but have not uncovered their underlying organizations. This leaves open a scientific question: "how feature-specific visual information is distributed across neural populations in higher visual areas, and whether it is organized into structured, semantically meaningful subspaces." To tackle this problem, we present MIG-Vis, a method that leverages the generative power of diffusion models to visualize and validate the visual-semantic attributes encoded in neural latent subspaces. Our method first uses a variational autoencoder to infer a group-wise disentangled neural latent subspace from neural populations. Subsequently, we propose a mutual information (MI)-guided diffusion synthesis procedure to visualize the specific visual-semantic features encoded by each latent group. We validate MIG-Vis on multi-session neural spiking datasets from the inferior temporal (IT) cortex of two macaques. The synthesized results demonstrate that our method identifies neural latent groups with clear semantic selectivity to diverse visual features, including object pose, inter-category transformations, and intra-class content. These findings provide direct, interpretable evidence of structured semantic representation in the higher visual cortex and advance our understanding of its encoding principles.

Fast and Generalizable parameter-embedded Neural Operators for Lithium-Ion Battery Simulation

Reliable digital twins of lithium-ion batteries must achieve high physical fidelity with sub-millisecond speed. In this work, we benchmark three operator-learning surrogates for the Single Particle Model (SPM): Deep Operator Networks (DeepONets), Fourier Neural Operators (FNOs) and a newly proposed parameter-embedded Fourier Neural Operator (PE-FNO), which conditions each spectral layer on particle radius and solid-phase diffusivity. Models are trained on simulated trajectories spanning four current families (constant, triangular, pulse-train, and Gaussian-random-field) and a full range of State-of-Charge (SOC) (0 % to 100 %). DeepONet accurately replicates constant-current behaviour but struggles with more dynamic loads. The basic FNO maintains mesh invariance and keeps concentration errors below 1 %, with voltage mean-absolute errors under 1.7 mV across all load types. Introducing parameter embedding marginally increases error, but enables generalisation to varying radii and diffusivities. PE-FNO executes approximately 200 times faster than a 16-thread SPM solver. Consequently, PE-FNO's capabilities in inverse tasks are explored in a parameter estimation task with Bayesian optimisation, recovering anode and cathode diffusivities with 1.14 % and 8.4 % mean absolute percentage error, respectively, and 0.5918 percentage points higher error in comparison with classical methods. These results pave the way for neural operators to meet the accuracy, speed and parametric flexibility demands of real-time battery management, design-of-experiments and large-scale inference. PE-FNO outperforms conventional neural surrogates, offering a practical path towards high-speed and high-fidelity electrochemical digital twins.

A Revisit of Total Correlation in Disentangled Variational Auto-Encoder with Partial Disentanglement

A fully disentangled variational auto-encoder (VAE) aims to identify disentangled latent components from observations. However, enforcing full independence between all latent components may be too strict for certain datasets. In some cases, multiple factors may be entangled together in a non-separable manner, or a single independent semantic meaning could be represented by multiple latent components within a higher-dimensional manifold. To address such scenarios with greater flexibility, we develop the Partially Disentangled VAE (PDisVAE), which generalizes the total correlation (TC) term in fully disentangled VAEs to a partial correlation (PC) term. This framework can handle group-wise independence and can naturally reduce to either the standard VAE or the fully disentangled VAE. Validation through three synthetic experiments demonstrates the correctness and practicality of PDisVAE. When applied to real-world datasets, PDisVAE discovers valuable information that is difficult to find using fully disentangled VAEs, implying its versatility and effectiveness.

Assessing the Robustness of Retrieval-Augmented Generation Systems in K-12 Educational Question Answering with Knowledge Discrepancies

Retrieval-Augmented Generation (RAG) systems have demonstrated remarkable potential as question answering systems in the K-12 Education domain, where knowledge is typically queried within the restricted scope of authoritative textbooks. However, the discrepancy between textbooks and the parametric knowledge in Large Language Models (LLMs) could undermine the effectiveness of RAG systems. To systematically investigate the robustness of RAG systems under such knowledge discrepancies, we present EduKDQA, a question answering dataset that simulates knowledge discrepancies in real applications by applying hypothetical knowledge updates in answers and source documents. EduKDQA includes 3,005 questions covering five subjects, under a comprehensive question typology from the perspective of context utilization and knowledge integration. We conducted extensive experiments on retrieval and question answering performance. We find that most RAG systems suffer from a substantial performance drop in question answering with knowledge discrepancies, while questions that require integration of contextual knowledge and parametric knowledge pose a challenge to LLMs.

Efficient and Comprehensive Feature Extraction in Large Vision-Language Model for Clinical Pathology Analysis

Pathological diagnosis is vital for determining disease characteristics, guiding treatment, and assessing prognosis, relying heavily on detailed, multi-scale analysis of high-resolution whole slide images (WSI). However, traditional pure vision models face challenges of redundant feature extraction, whereas existing large vision-language models (LVLMs) are limited by input resolution constraints, hindering their efficiency and accuracy. To overcome these issues, we propose two innovative strategies: the mixed task-guided feature enhancement, which directs feature extraction toward lesion-related details across scales, and the prompt-guided detail feature completion, which integrates coarse- and fine-grained features from WSI based on specific prompts without compromising inference speed. Leveraging a comprehensive dataset of 490,000 samples from diverse pathology tasks-including cancer detection, grading, vascular and neural invasion identification, and so on-we trained the pathology-specialized LVLM, OmniPath. Extensive experiments demonstrate that this model significantly outperforms existing methods in diagnostic accuracy and efficiency, offering an interactive, clinically aligned approach for auxiliary diagnosis in a wide range of pathology applications.

Exploring Behavior-Relevant and Disentangled Neural Dynamics with Generative Diffusion Models

Understanding the neural basis of behavior is a fundamental goal in neuroscience. Current research in large-scale neuro-behavioral data analysis often relies on decoding models, which quantify behavioral information in neural data but lack details on behavior encoding. This raises an intriguing scientific question: ``how can we enable in-depth exploration of neural representations in behavioral tasks, revealing interpretable neural dynamics associated with behaviors''. However, addressing this issue is challenging due to the varied behavioral encoding across different brain regions and mixed selectivity at the population level. To tackle this limitation, our approach, named ``BeNeDiff'', first identifies a fine-grained and disentangled neural subspace using a behavior-informed latent variable model. It then employs state-of-the-art generative diffusion models to synthesize behavior videos that interpret the neural dynamics of each latent factor. We validate the method on multi-session datasets containing widefield calcium imaging recordings across the dorsal cortex. Through guiding the diffusion model to activate individual latent factors, we verify that the neural dynamics of latent factors in the disentangled neural subspace provide interpretable quantifications of the behaviors of interest. At the same time, the neural subspace in BeNeDiff demonstrates high disentanglement and neural reconstruction quality.

Markovian Gaussian Process: A Universal State-Space Representation for Stationary Temporal Gaussian Process

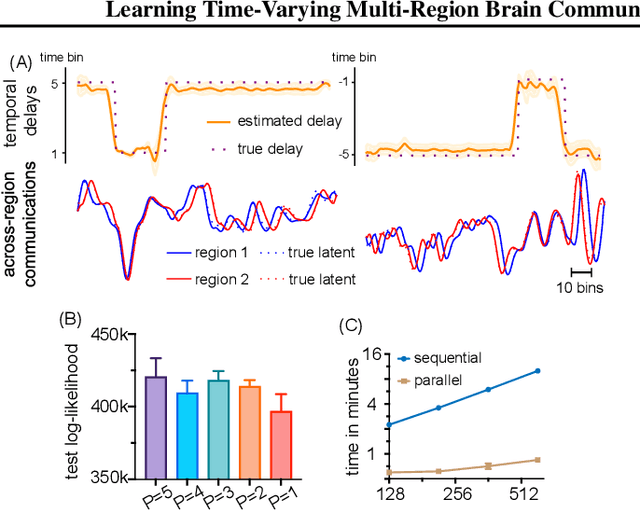
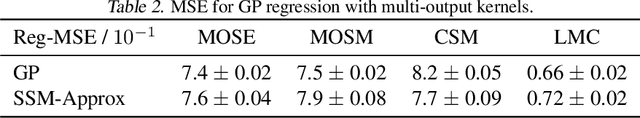
Gaussian Processes (GPs) and Linear Dynamical Systems (LDSs) are essential time series and dynamic system modeling tools. GPs can handle complex, nonlinear dynamics but are computationally demanding, while LDSs offer efficient computation but lack the expressive power of GPs. To combine their benefits, we introduce a universal method that allows an LDS to mirror stationary temporal GPs. This state-space representation, known as the Markovian Gaussian Process (Markovian GP), leverages the flexibility of kernel functions while maintaining efficient linear computation. Unlike existing GP-LDS conversion methods, which require separability for most multi-output kernels, our approach works universally for single- and multi-output stationary temporal kernels. We evaluate our method by computing covariance, performing regression tasks, and applying it to a neuroscience application, demonstrating that our method provides an accurate state-space representation for stationary temporal GPs.

A Differentiable Partially Observable Generalized Linear Model with Forward-Backward Message Passing

The partially observable generalized linear model (POGLM) is a powerful tool for understanding neural connectivity under the assumption of existing hidden neurons. With spike trains only recorded from visible neurons, existing works use variational inference to learn POGLM meanwhile presenting the difficulty of learning this latent variable model. There are two main issues: (1) the sampled Poisson hidden spike count hinders the use of the pathwise gradient estimator in VI; and (2) the existing design of the variational model is neither expressive nor time-efficient, which further affects the performance. For (1), we propose a new differentiable POGLM, which enables the pathwise gradient estimator, better than the score function gradient estimator used in existing works. For (2), we propose the forward-backward message-passing sampling scheme for the variational model. Comprehensive experiments show that our differentiable POGLMs with our forward-backward message passing produce a better performance on one synthetic and two real-world datasets. Furthermore, our new method yields more interpretable parameters, underscoring its significance in neuroscience.

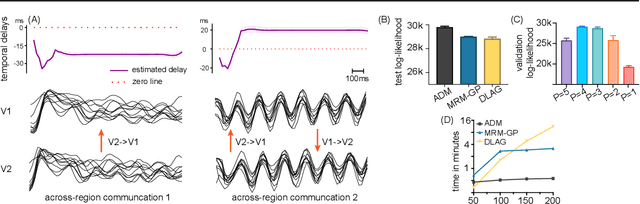
Multi-Region Markovian Gaussian Process: An Efficient Method to Discover Directional Communications Across Multiple Brain Regions

Studying the complex interactions between different brain regions is crucial in neuroscience. Various statistical methods have explored the latent communication across multiple brain regions. Two main categories are the Gaussian Process (GP) and Linear Dynamical System (LDS), each with unique strengths. The GP-based approach effectively discovers latent variables such as frequency bands and communication directions. Conversely, the LDS-based approach is computationally efficient but lacks powerful expressiveness in latent representation. In this study, we merge both methodologies by creating an LDS mirroring a multi-output GP, termed Multi-Region Markovian Gaussian Process (MRM-GP). Our work is the first to establish a connection between an LDS and a multi-output GP that explicitly models frequencies and phase delays within the latent space of neural recordings. Consequently, the model achieves a linear inference cost over time points and provides an interpretable low-dimensional representation, revealing communication directions across brain regions and separating oscillatory communications into different frequency bands.