Exploring Behavior-Relevant and Disentangled Neural Dynamics with Generative Diffusion Models

Understanding the neural basis of behavior is a fundamental goal in neuroscience. Current research in large-scale neuro-behavioral data analysis often relies on decoding models, which quantify behavioral information in neural data but lack details on behavior encoding. This raises an intriguing scientific question: ``how can we enable in-depth exploration of neural representations in behavioral tasks, revealing interpretable neural dynamics associated with behaviors''. However, addressing this issue is challenging due to the varied behavioral encoding across different brain regions and mixed selectivity at the population level. To tackle this limitation, our approach, named ``BeNeDiff'', first identifies a fine-grained and disentangled neural subspace using a behavior-informed latent variable model. It then employs state-of-the-art generative diffusion models to synthesize behavior videos that interpret the neural dynamics of each latent factor. We validate the method on multi-session datasets containing widefield calcium imaging recordings across the dorsal cortex. Through guiding the diffusion model to activate individual latent factors, we verify that the neural dynamics of latent factors in the disentangled neural subspace provide interpretable quantifications of the behaviors of interest. At the same time, the neural subspace in BeNeDiff demonstrates high disentanglement and neural reconstruction quality.

Markovian Gaussian Process: A Universal State-Space Representation for Stationary Temporal Gaussian Process

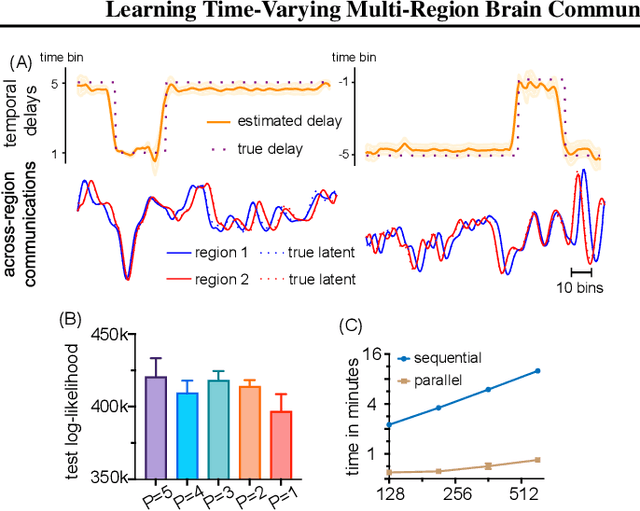
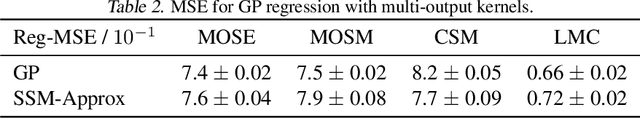
Gaussian Processes (GPs) and Linear Dynamical Systems (LDSs) are essential time series and dynamic system modeling tools. GPs can handle complex, nonlinear dynamics but are computationally demanding, while LDSs offer efficient computation but lack the expressive power of GPs. To combine their benefits, we introduce a universal method that allows an LDS to mirror stationary temporal GPs. This state-space representation, known as the Markovian Gaussian Process (Markovian GP), leverages the flexibility of kernel functions while maintaining efficient linear computation. Unlike existing GP-LDS conversion methods, which require separability for most multi-output kernels, our approach works universally for single- and multi-output stationary temporal kernels. We evaluate our method by computing covariance, performing regression tasks, and applying it to a neuroscience application, demonstrating that our method provides an accurate state-space representation for stationary temporal GPs.

A Differentiable Partially Observable Generalized Linear Model with Forward-Backward Message Passing

The partially observable generalized linear model (POGLM) is a powerful tool for understanding neural connectivity under the assumption of existing hidden neurons. With spike trains only recorded from visible neurons, existing works use variational inference to learn POGLM meanwhile presenting the difficulty of learning this latent variable model. There are two main issues: (1) the sampled Poisson hidden spike count hinders the use of the pathwise gradient estimator in VI; and (2) the existing design of the variational model is neither expressive nor time-efficient, which further affects the performance. For (1), we propose a new differentiable POGLM, which enables the pathwise gradient estimator, better than the score function gradient estimator used in existing works. For (2), we propose the forward-backward message-passing sampling scheme for the variational model. Comprehensive experiments show that our differentiable POGLMs with our forward-backward message passing produce a better performance on one synthetic and two real-world datasets. Furthermore, our new method yields more interpretable parameters, underscoring its significance in neuroscience.

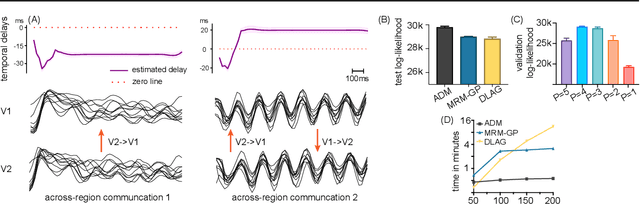
Multi-Region Markovian Gaussian Process: An Efficient Method to Discover Directional Communications Across Multiple Brain Regions

Studying the complex interactions between different brain regions is crucial in neuroscience. Various statistical methods have explored the latent communication across multiple brain regions. Two main categories are the Gaussian Process (GP) and Linear Dynamical System (LDS), each with unique strengths. The GP-based approach effectively discovers latent variables such as frequency bands and communication directions. Conversely, the LDS-based approach is computationally efficient but lacks powerful expressiveness in latent representation. In this study, we merge both methodologies by creating an LDS mirroring a multi-output GP, termed Multi-Region Markovian Gaussian Process (MRM-GP). Our work is the first to establish a connection between an LDS and a multi-output GP that explicitly models frequencies and phase delays within the latent space of neural recordings. Consequently, the model achieves a linear inference cost over time points and provides an interpretable low-dimensional representation, revealing communication directions across brain regions and separating oscillatory communications into different frequency bands.

Forward $χ^2$ Divergence Based Variational Importance Sampling

Maximizing the log-likelihood is a crucial aspect of learning latent variable models, and variational inference (VI) stands as the commonly adopted method. However, VI can encounter challenges in achieving a high log-likelihood when dealing with complicated posterior distributions. In response to this limitation, we introduce a novel variational importance sampling (VIS) approach that directly estimates and maximizes the log-likelihood. VIS leverages the optimal proposal distribution, achieved by minimizing the forward $\chi^2$ divergence, to enhance log-likelihood estimation. We apply VIS to various popular latent variable models, including mixture models, variational auto-encoders, and partially observable generalized linear models. Results demonstrate that our approach consistently outperforms state-of-the-art baselines, both in terms of log-likelihood and model parameter estimation.

One-hot Generalized Linear Model for Switching Brain State Discovery

Exposing meaningful and interpretable neural interactions is critical to understanding neural circuits. Inferred neural interactions from neural signals primarily reflect functional interactions. In a long experiment, subject animals may experience different stages defined by the experiment, stimuli, or behavioral states, and hence functional interactions can change over time. To model dynamically changing functional interactions, prior work employs state-switching generalized linear models with hidden Markov models (i.e., HMM-GLMs). However, we argue they lack biological plausibility, as functional interactions are shaped and confined by the underlying anatomical connectome. Here, we propose a novel prior-informed state-switching GLM. We introduce both a Gaussian prior and a one-hot prior over the GLM in each state. The priors are learnable. We will show that the learned prior should capture the state-constant interaction, shedding light on the underlying anatomical connectome and revealing more likely physical neuron interactions. The state-dependent interaction modeled by each GLM offers traceability to capture functional variations across multiple brain states. Our methods effectively recover true interaction structures in simulated data, achieve the highest predictive likelihood with real neural datasets, and render interaction structures and hidden states more interpretable when applied to real neural data.

Extraction and Recovery of Spatio-Temporal Structure in Latent Dynamics Alignment with Diffusion Model

In the field of behavior-related brain computation, it is necessary to meaningfully align raw neural population activities against the drastic shift between them. However, the alignment is non-trivial since most neural population activities are in a multivariate time-series manner. An instrumental framework within neuroscience research posits that trial-based neural population activities rely on low-dimensional latent dynamics. Focusing on such latent dynamics greatly facilitates the alignment procedure. Despite the considerable progress we have reached, existing methods usually ignore the intrinsic spatio-temporal structures within latent dynamics. Thus, those solutions lead to poor quality in dynamics structures and overall performance after alignment. To tackle this problem, we propose a method leveraging the expressiveness of diffusion model to relieve such issues. Specifically, the latent dynamics structures of the source domain are first extracted by the diffusion model. Then, such structures are well-recovered through a maximum likelihood alignment procedure on the target domain. We first demonstrate the effectiveness of our proposed method on a synthetic dataset. Then, when applied to neural recordings from primate motor cortex, under both cross-day and inter-subject settings, our method consistently manifests its capability of preserving the spatio-temporal structure of latent dynamics and outperforms existing approaches in alignment quality.

Inverse Kernel Decomposition

The state-of-the-art dimensionality reduction approaches largely rely on complicated optimization procedures. On the other hand, closed-form approaches requiring merely eigen-decomposition do not have enough sophistication and nonlinearity. In this paper, we propose a novel nonlinear dimensionality reduction method -- Inverse Kernel Decomposition (IKD) -- based on an eigen-decomposition of the sample covariance matrix of data. The method is inspired by Gaussian process latent variable models (GPLVMs) and has comparable performance with GPLVMs. To deal with very noisy data with weak correlations, we propose two solutions -- blockwise and geodesic -- to make use of locally correlated data points and provide better and numerically more stable latent estimations. We use synthetic datasets and four real-world datasets to show that IKD is a better dimensionality reduction method than other eigen-decomposition-based methods, and achieves comparable performance against optimization-based methods with faster running speeds. Open-source IKD implementation in Python can be accessed at this \url{https://github.com/JerrySoybean/ikd}.