ClozeMath: Improving Mathematical Reasoning in Language Models by Learning to Fill Equations

The capabilities of large language models (LLMs) have been enhanced by training on data that reflects human thought processes, such as the Chain-of-Thought format. However, evidence suggests that the conventional scheme of next-word prediction may not fully capture how humans learn to think. Inspired by how humans generalize mathematical reasoning, we propose a new approach named ClozeMath to fine-tune LLMs for mathematical reasoning. Our ClozeMath involves a text-infilling task that predicts masked equations from a given solution, analogous to cloze exercises used in human learning. Experiments on GSM8K, MATH, and GSM-Symbolic show that ClozeMath surpasses the strong baseline Masked Thought in performance and robustness, with two test-time scaling decoding algorithms, Beam Search and Chain-of-Thought decoding. Additionally, we conduct an ablation study to analyze the effects of various architectural and implementation choices on our approach.

On Barycenter Computation: Semi-Unbalanced Optimal Transport-based Method on Gaussians

We explore a robust version of the barycenter problem among $n$ centered Gaussian probability measures, termed Semi-Unbalanced Optimal Transport (SUOT)-based Barycenter, wherein the barycenter remains fixed while the others are relaxed using Kullback-Leibler divergence. We develop optimization algorithms on Bures-Wasserstein manifold, named the Exact Geodesic Gradient Descent and Hybrid Gradient Descent algorithms. While the Exact Geodesic Gradient Descent method is based on computing the exact closed form of the first-order derivative of the objective function of the barycenter along a geodesic on the Bures manifold, the Hybrid Gradient Descent method utilizes optimizer components when solving the SUOT problem to replace outlier measures before applying the Riemannian Gradient Descent. We establish the theoretical convergence guarantees for both methods and demonstrate that the Exact Geodesic Gradient Descent algorithm attains a dimension-free convergence rate. Finally, we conduct experiments to compare the normal Wasserstein Barycenter with ours and perform an ablation study.

Diversity-Aware Agnostic Ensemble of Sharpness Minimizers

There has long been plenty of theoretical and empirical evidence supporting the success of ensemble learning. Deep ensembles in particular take advantage of training randomness and expressivity of individual neural networks to gain prediction diversity, ultimately leading to better generalization, robustness and uncertainty estimation. In respect of generalization, it is found that pursuing wider local minima result in models being more robust to shifts between training and testing sets. A natural research question arises out of these two approaches as to whether a boost in generalization ability can be achieved if ensemble learning and loss sharpness minimization are integrated. Our work investigates this connection and proposes DASH - a learning algorithm that promotes diversity and flatness within deep ensembles. More concretely, DASH encourages base learners to move divergently towards low-loss regions of minimal sharpness. We provide a theoretical backbone for our method along with extensive empirical evidence demonstrating an improvement in ensemble generalizability.

Robust Diffusion GAN using Semi-Unbalanced Optimal Transport

Diffusion models, a type of generative model, have demonstrated great potential for synthesizing highly detailed images. By integrating with GAN, advanced diffusion models like DDGAN \citep{xiao2022DDGAN} could approach real-time performance for expansive practical applications. While DDGAN has effectively addressed the challenges of generative modeling, namely producing high-quality samples, covering different data modes, and achieving faster sampling, it remains susceptible to performance drops caused by datasets that are corrupted with outlier samples. This work introduces a robust training technique based on semi-unbalanced optimal transport to mitigate the impact of outliers effectively. Through comprehensive evaluations, we demonstrate that our robust diffusion GAN (RDGAN) outperforms vanilla DDGAN in terms of the aforementioned generative modeling criteria, i.e., image quality, mode coverage of distribution, and inference speed, and exhibits improved robustness when dealing with both clean and corrupted datasets.

Robust Contrastive Learning With Theory Guarantee

Contrastive learning (CL) is a self-supervised training paradigm that allows us to extract meaningful features without any label information. A typical CL framework is divided into two phases, where it first tries to learn the features from unlabelled data, and then uses those features to train a linear classifier with the labeled data. While a fair amount of existing theoretical works have analyzed how the unsupervised loss in the first phase can support the supervised loss in the second phase, none has examined the connection between the unsupervised loss and the robust supervised loss, which can shed light on how to construct an effective unsupervised loss for the first phase of CL. To fill this gap, our work develops rigorous theories to dissect and identify which components in the unsupervised loss can help improve the robust supervised loss and conduct proper experiments to verify our findings.

Understanding the Robustness of Randomized Feature Defense Against Query-Based Adversarial Attacks

Recent works have shown that deep neural networks are vulnerable to adversarial examples that find samples close to the original image but can make the model misclassify. Even with access only to the model's output, an attacker can employ black-box attacks to generate such adversarial examples. In this work, we propose a simple and lightweight defense against black-box attacks by adding random noise to hidden features at intermediate layers of the model at inference time. Our theoretical analysis confirms that this method effectively enhances the model's resilience against both score-based and decision-based black-box attacks. Importantly, our defense does not necessitate adversarial training and has minimal impact on accuracy, rendering it applicable to any pre-trained model. Our analysis also reveals the significance of selectively adding noise to different parts of the model based on the gradient of the adversarial objective function, which can be varied during the attack. We demonstrate the robustness of our defense against multiple black-box attacks through extensive empirical experiments involving diverse models with various architectures.

RSAM: Learning on manifolds with Riemannian Sharpness-aware Minimization

Nowadays, understanding the geometry of the loss landscape shows promise in enhancing a model's generalization ability. In this work, we draw upon prior works that apply geometric principles to optimization and present a novel approach to improve robustness and generalization ability for constrained optimization problems. Indeed, this paper aims to generalize the Sharpness-Aware Minimization (SAM) optimizer to Riemannian manifolds. In doing so, we first extend the concept of sharpness and introduce a novel notion of sharpness on manifolds. To support this notion of sharpness, we present a theoretical analysis characterizing generalization capabilities with respect to manifold sharpness, which demonstrates a tighter bound on the generalization gap, a result not known before. Motivated by this analysis, we introduce our algorithm, Riemannian Sharpness-Aware Minimization (RSAM). To demonstrate RSAM's ability to enhance generalization ability, we evaluate and contrast our algorithm on a broad set of problems, such as image classification and contrastive learning across different datasets, including CIFAR100, CIFAR10, and FGVCAircraft. Our code is publicly available at \url{https://t.ly/RiemannianSAM}.

Sharpness & Shift-Aware Self-Supervised Learning

Self-supervised learning aims to extract meaningful features from unlabeled data for further downstream tasks. In this paper, we consider classification as a downstream task in phase 2 and develop rigorous theories to realize the factors that implicitly influence the general loss of this classification task. Our theories signify that sharpness-aware feature extractors benefit the classification task in phase 2 and the existing data shift between the ideal (i.e., the ideal one used in theory development) and practical (i.e., the practical one used in implementation) distributions to generate positive pairs also remarkably affects this classification task. Further harvesting these theoretical findings, we propose to minimize the sharpness of the feature extractor and a new Fourier-based data augmentation technique to relieve the data shift in the distributions generating positive pairs, reaching Sharpness & Shift-Aware Contrastive Learning (SSA-CLR). We conduct extensive experiments to verify our theoretical findings and demonstrate that sharpness & shift-aware contrastive learning can remarkably boost the performance as well as obtaining more robust extracted features compared with the baselines.

Entropic Gromov-Wasserstein between Gaussian Distributions

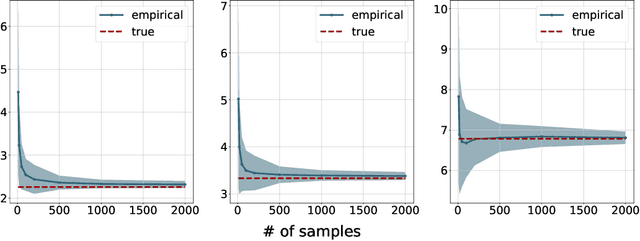
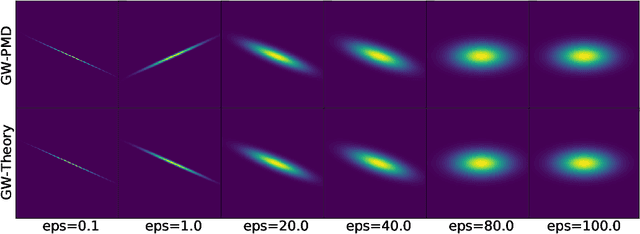
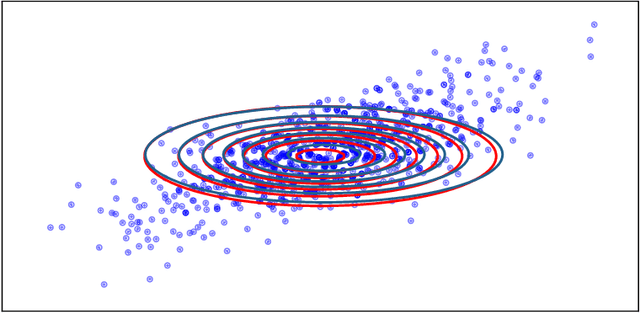
We study the entropic Gromov-Wasserstein and its unbalanced version between (unbalanced) Gaussian distributions with different dimensions. When the metric is the inner product, which we refer to as inner product Gromov-Wasserstein (IGW), we demonstrate that the optimal transportation plans of entropic IGW and its unbalanced variant are (unbalanced) Gaussian distributions. Via an application of von Neumann's trace inequality, we obtain closed-form expressions for the entropic IGW between these Gaussian distributions. Finally, we consider an entropic inner product Gromov-Wasserstein barycenter of multiple Gaussian distributions. We prove that the barycenter is Gaussian distribution when the entropic regularization parameter is small. We further derive closed-form expressions for the covariance matrix of the barycenter.

An Efficient Mini-batch Method via Partial Transportation

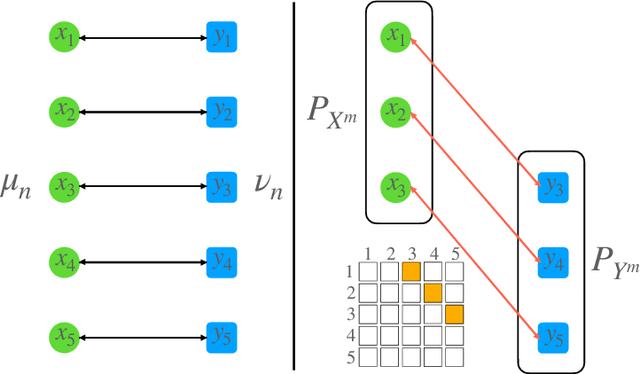
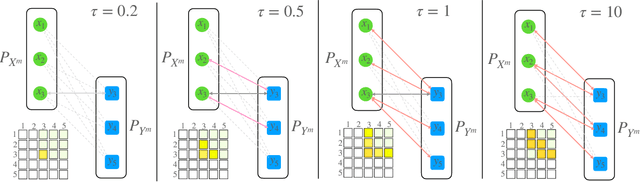
Mini-batch optimal transport (m-OT) has been widely used recently to deal with the memory issue of OT in large-scale applications. Despite their practicality, m-OT suffers from misspecified mappings, namely, mappings that are optimal on the mini-batch level but do not exist in the optimal transportation plan between the original measures. To address the misspecified mappings issue, we propose a novel mini-batch method by using partial optimal transport (POT) between mini-batch empirical measures, which we refer to as mini-batch partial optimal transport (m-POT). Leveraging the insight from the partial transportation, we explain the source of misspecified mappings from the m-OT and motivate why limiting the amount of transported masses among mini-batches via POT can alleviate the incorrect mappings. Finally, we carry out extensive experiments on various applications to compare m-POT with m-OT and recently proposed mini-batch method, mini-batch unbalanced optimal transport (m-UOT). We observe that m-POT is better than m-OT deep domain adaptation applications while having comparable performance with m-UOT. On other applications, such as deep generative model, gradient flow, and color transfer, m-POT yields more favorable performance than both m-OT and m-UOT.