Model-based causal feature selection for general response types

Discovering causal relationships from observational data is a fundamental yet challenging task. In some applications, it may suffice to learn the causal features of a given response variable, instead of learning the entire underlying causal structure. Invariant causal prediction (ICP, Peters et al., 2016) is a method for causal feature selection which requires data from heterogeneous settings. ICP assumes that the mechanism for generating the response from its direct causes is the same in all settings and exploits this invariance to output a subset of the causal features. The framework of ICP has been extended to general additive noise models and to nonparametric settings using conditional independence testing. However, nonparametric conditional independence testing often suffers from low power (or poor type I error control) and the aforementioned parametric models are not suitable for applications in which the response is not measured on a continuous scale, but rather reflects categories or counts. To bridge this gap, we develop ICP in the context of transformation models (TRAMs), allowing for continuous, categorical, count-type, and uninformatively censored responses (we show that, in general, these model classes do not allow for identifiability when there is no exogenous heterogeneity). We propose TRAM-GCM, a test for invariance of a subset of covariates, based on the expected conditional covariance between environments and score residuals which satisfies uniform asymptotic level guarantees. For the special case of linear shift TRAMs, we propose an additional invariance test, TRAM-Wald, based on the Wald statistic. We implement both proposed methods in the open-source R package "tramicp" and show in simulations that under the correct model specification, our approach empirically yields higher power than nonparametric ICP based on conditional independence testing.

Deep conditional transformation models for survival analysis

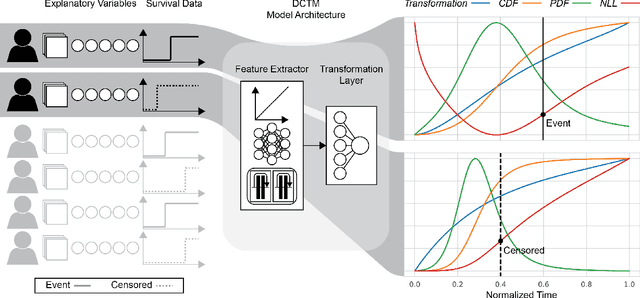
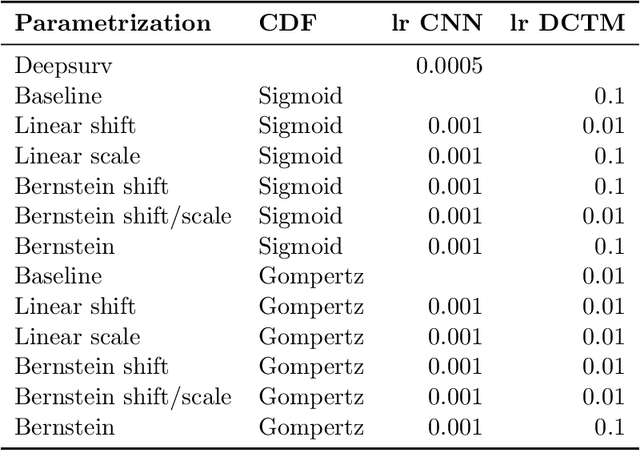
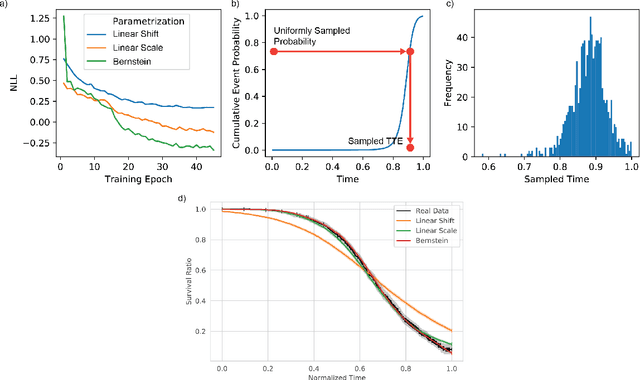
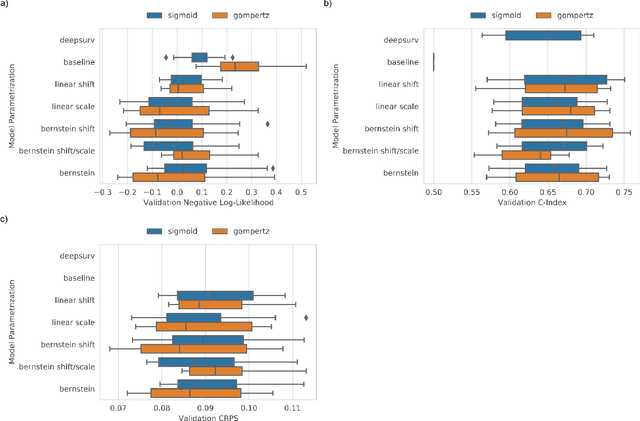
An every increasing number of clinical trials features a time-to-event outcome and records non-tabular patient data, such as magnetic resonance imaging or text data in the form of electronic health records. Recently, several neural-network based solutions have been proposed, some of which are binary classifiers. Parametric, distribution-free approaches which make full use of survival time and censoring status have not received much attention. We present deep conditional transformation models (DCTMs) for survival outcomes as a unifying approach to parametric and semiparametric survival analysis. DCTMs allow the specification of non-linear and non-proportional hazards for both tabular and non-tabular data and extend to all types of censoring and truncation. On real and semi-synthetic data, we show that DCTMs compete with state-of-the-art DL approaches to survival analysis.

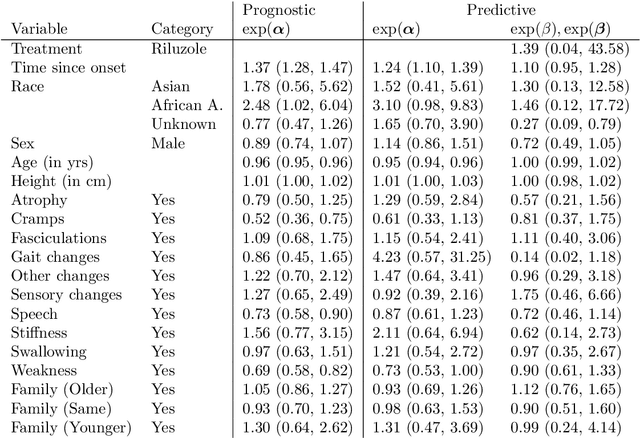
Heterogeneous Treatment Effect Estimation for Observational Data using Model-based Forests

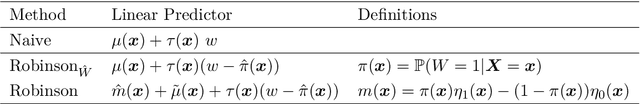
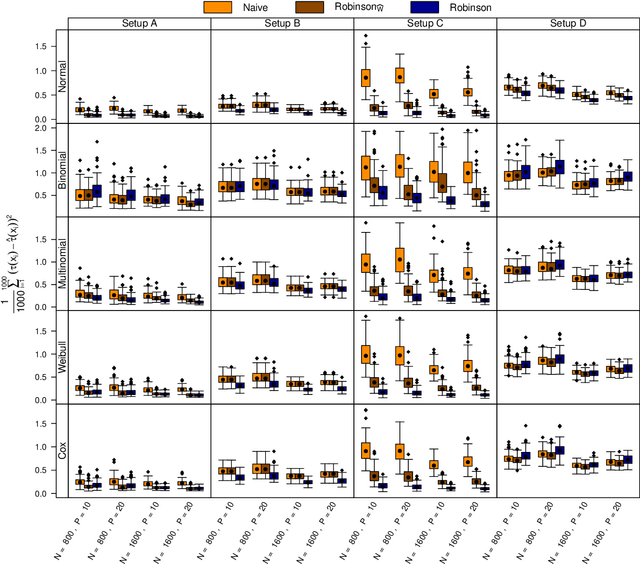
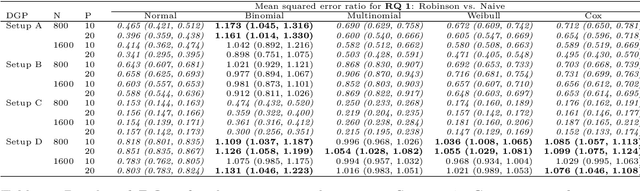
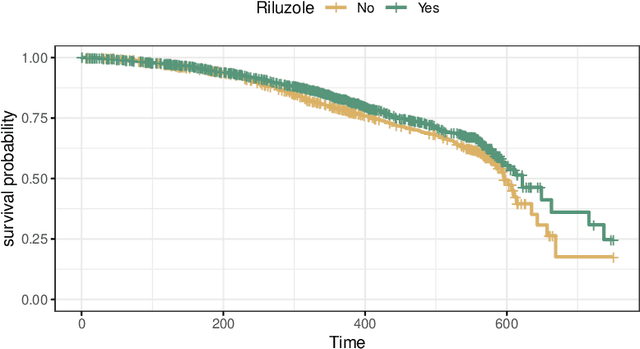
The estimation of heterogeneous treatment effects (HTEs) has attracted considerable interest in many disciplines, most prominently in medicine and economics. Contemporary research has so far primarily focused on continuous and binary responses where HTEs are traditionally estimated by a linear model, which allows the estimation of constant or heterogeneous effects even under certain model misspecifications. More complex models for survival, count, or ordinal outcomes require stricter assumptions to reliably estimate the treatment effect. Most importantly, the noncollapsibility issue necessitates the joint estimation of treatment and prognostic effects. Model-based forests allow simultaneous estimation of covariate-dependent treatment and prognostic effects, but only for randomized trials. In this paper, we propose modifications to model-based forests to address the confounding issue in observational data. In particular, we evaluate an orthogonalization strategy originally proposed by Robinson (1988, Econometrica) in the context of model-based forests targeting HTE estimation in generalized linear models and transformation models. We found that this strategy reduces confounding effects in a simulated study with various outcome distributions. We demonstrate the practical aspects of HTE estimation for survival and ordinal outcomes by an assessment of the potentially heterogeneous effect of Riluzole on the progress of Amyotrophic Lateral Sclerosis.

What Makes Forest-Based Heterogeneous Treatment Effect Estimators Work?

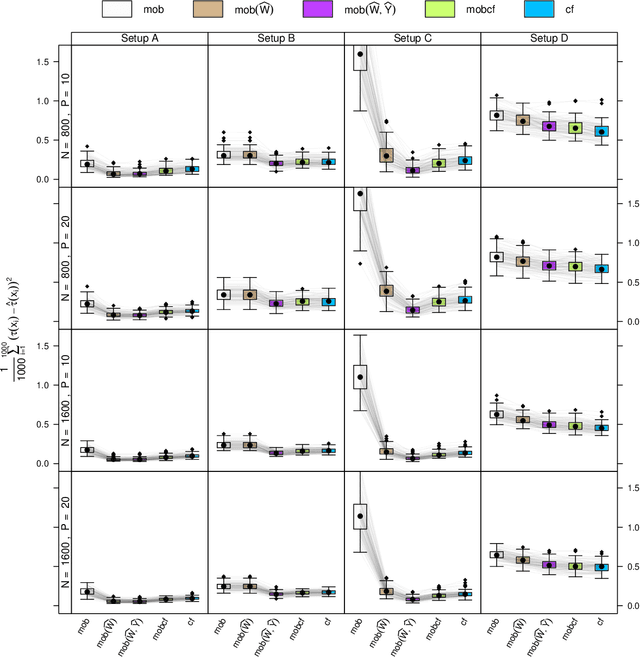
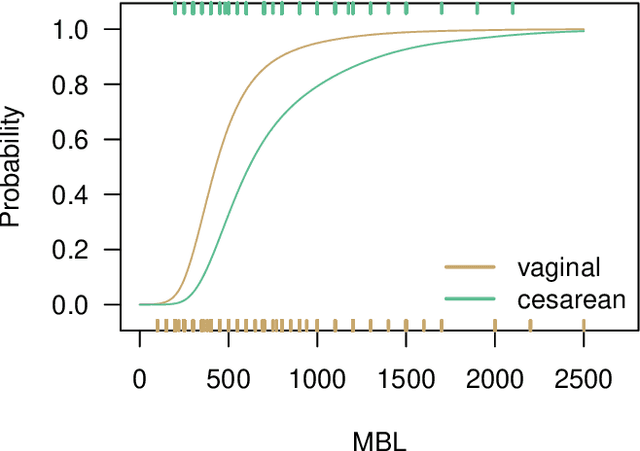
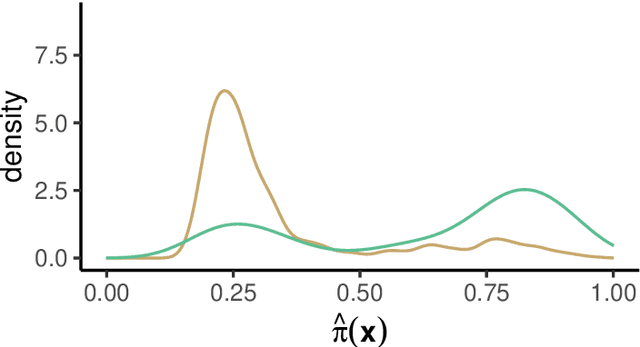
Estimation of heterogeneous treatment effects (HTE) is of prime importance in many disciplines, ranging from personalized medicine to economics among many others. Random forests have been shown to be a flexible and powerful approach to HTE estimation in both randomized trials and observational studies. In particular "causal forests", introduced by Athey, Tibshirani and Wager (2019), along with the R implementation in package grf were rapidly adopted. A related approach, called "model-based forests", that is geared towards randomized trials and simultaneously captures effects of both prognostic and predictive variables, was introduced by Seibold, Zeileis and Hothorn (2018) along with a modular implementation in the R package model4you. Here, we present a unifying view that goes beyond the theoretical motivations and investigates which computational elements make causal forests so successful and how these can be blended with the strengths of model-based forests. To do so, we show that both methods can be understood in terms of the same parameters and model assumptions for an additive model under L2 loss. This theoretical insight allows us to implement several flavors of "model-based causal forests" and dissect their different elements in silico. The original causal forests and model-based forests are compared with the new blended versions in a benchmark study exploring both randomized trials and observational settings. In the randomized setting, both approaches performed akin. If confounding was present in the data generating process, we found local centering of the treatment indicator with the corresponding propensities to be the main driver for good performance. Local centering of the outcome was less important, and might be replaced or enhanced by simultaneous split selection with respect to both prognostic and predictive effects.

Deep interpretable ensembles

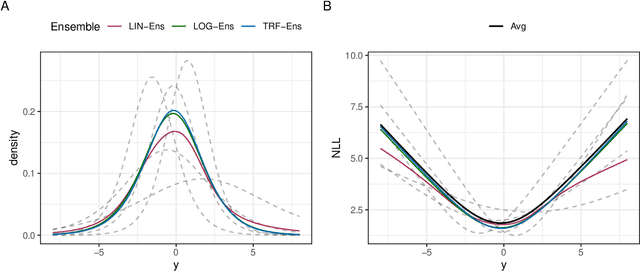
Ensembles improve prediction performance and allow uncertainty quantification by aggregating predictions from multiple models. In deep ensembling, the individual models are usually black box neural networks, or recently, partially interpretable semi-structured deep transformation models. However, interpretability of the ensemble members is generally lost upon aggregation. This is a crucial drawback of deep ensembles in high-stake decision fields, in which interpretable models are desired. We propose a novel transformation ensemble which aggregates probabilistic predictions with the guarantee to preserve interpretability and yield uniformly better predictions than the ensemble members on average. Transformation ensembles are tailored towards interpretable deep transformation models but are applicable to a wider range of probabilistic neural networks. In experiments on several publicly available data sets, we demonstrate that transformation ensembles perform on par with classical deep ensembles in terms of prediction performance, discrimination, and calibration. In addition, we demonstrate how transformation ensembles quantify both aleatoric and epistemic uncertainty, and produce minimax optimal predictions under certain conditions.

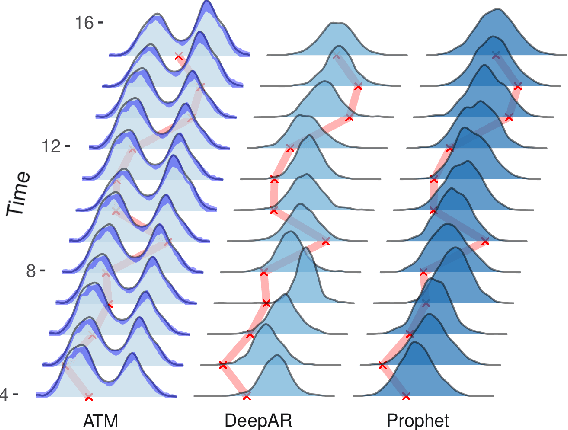
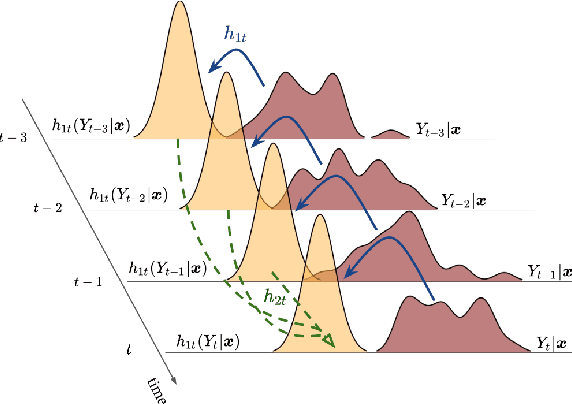
Transforming Autoregression: Interpretable and Expressive Time Series Forecast

Probabilistic forecasting of time series is an important matter in many applications and research fields. In order to draw conclusions from a probabilistic forecast, we must ensure that the model class used to approximate the true forecasting distribution is expressive enough. Yet, characteristics of the model itself, such as its uncertainty or its general functioning are not of lesser importance. In this paper, we propose Autoregressive Transformation Models (ATMs), a model class inspired from various research directions such as normalizing flows and autoregressive models. ATMs unite expressive distributional forecasts using a semi-parametric distribution assumption with an interpretable model specification and allow for uncertainty quantification based on (asymptotic) Maximum Likelihood theory. We demonstrate the properties of ATMs both theoretically and through empirical evaluation on several simulated and real-world forecasting datasets.

Ordinal Neural Network Transformation Models: Deep and interpretable regression models for ordinal outcomes

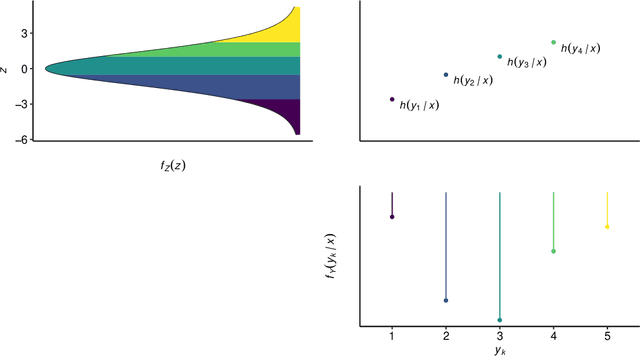
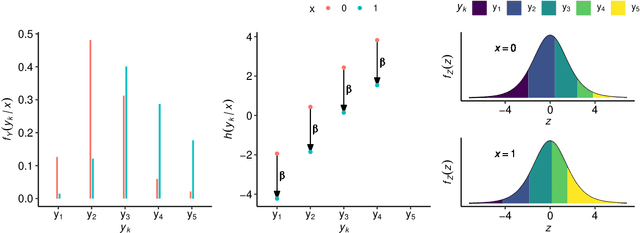
Outcomes with a natural order commonly occur in prediction tasks and oftentimes the available input data are a mixture of complex data, like images, and tabular predictors. Although deep Learning (DL) methods have shown outstanding performance on image classification, most models treat ordered outcomes as unordered and lack interpretability. In contrast, classical ordinal regression models yield interpretable predictor effects but are limited to tabular input data. Here, we present the highly modular class of ordinal neural network transformation models (ONTRAMs). Transformation models use a parametric transformation function and a simple distribution to trade off flexibility and interpretability of individual model components. In ONTRAMs, this trade-off is achieved by additively decomposing the transformation function into terms for the tabular and image data using a set of jointly trained neural networks. We show that the most flexible ONTRAMs achieve on-par performance with DL classifiers while outperforming them in training speed. We discuss how to interpret components of ONTRAMs in general and in the case of correlated tabular and image data. Taken together, ONTRAMs join benefits of DL and distributional regression to create interpretable prediction models for ordinal outcomes.

Deep Conditional Transformation Models

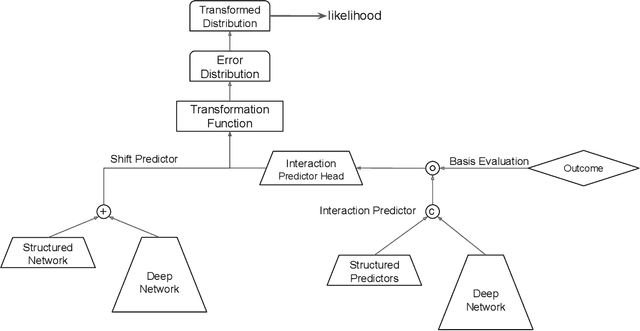
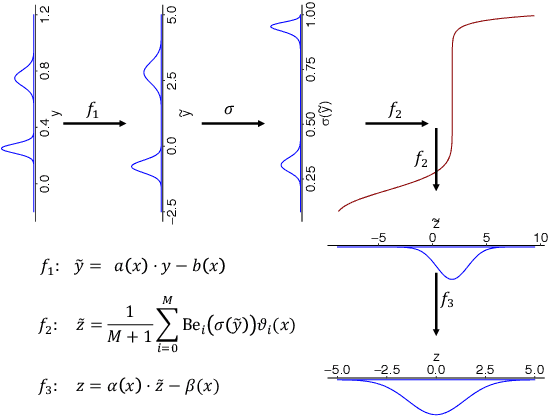
Learning the cumulative distribution function (CDF) of an outcome variable conditional on a set of features remains challenging, especially in high-dimensional settings. Conditional transformation models provide a semi-parametric approach that allows to model a large class of conditional CDFs without an explicit parametric distribution assumption and with only a few parameters. Existing estimation approaches within the class of transformation models are, however, either limited in their complexity and applicability to unstructured data sources such as images or text, or can incorporate complex effects of different features but lack interpretability. We close this gap by introducing the class of deep conditional transformation models which unify existing approaches and allow to learn both interpretable (non-)linear model terms and more complex predictors in one holistic neural network. To this end we propose a novel network architecture, provide details on different model definitions and derive suitable constraints and derive suitable network regularization terms. We demonstrate the efficacy of our approach through numerical experiments and applications.

Deep transformation models: Tackling complex regression problems with neural network based transformation models

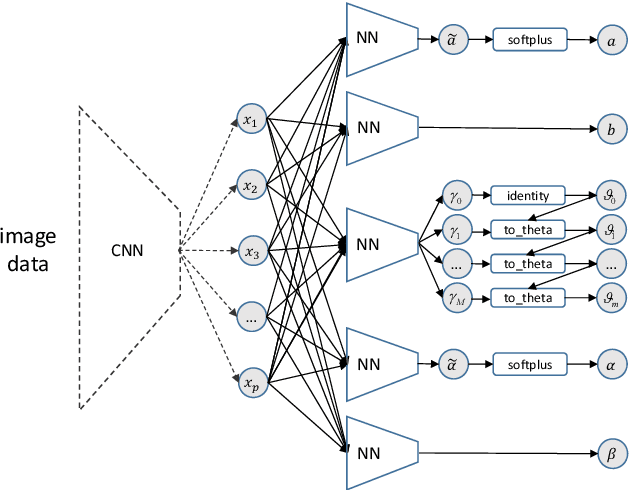
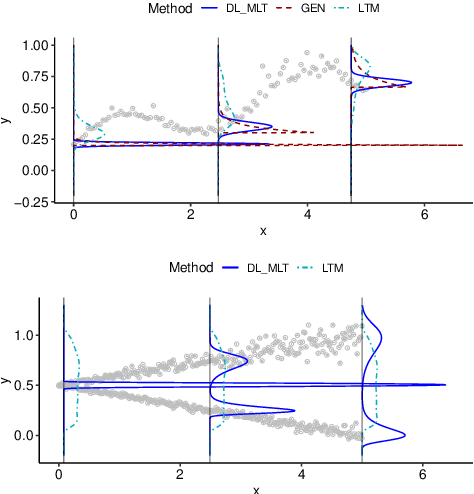
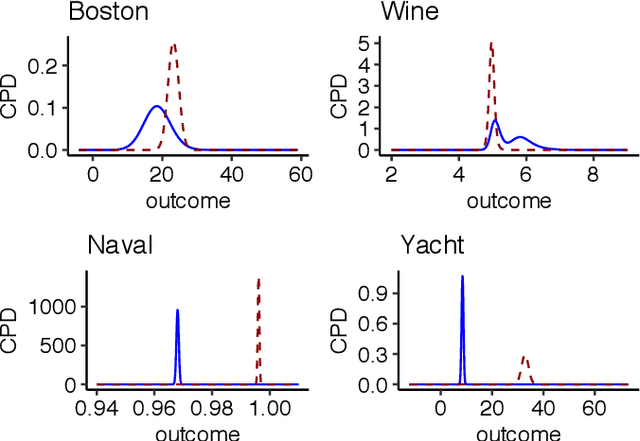
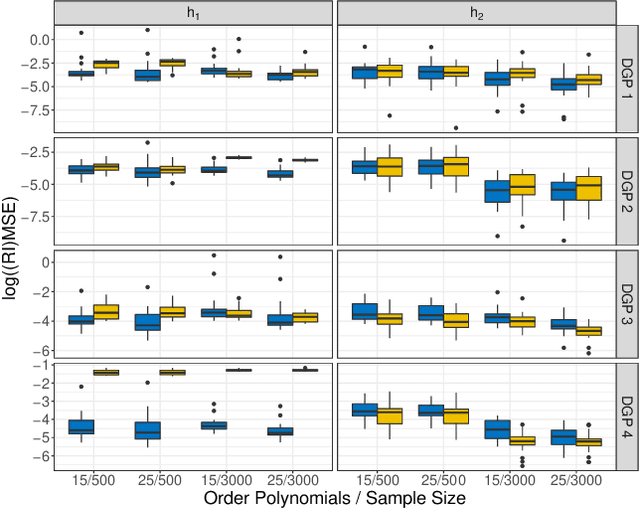
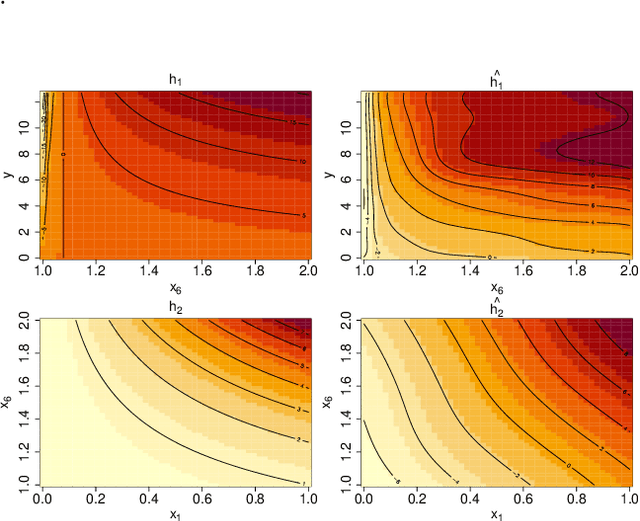
We present a deep transformation model for probabilistic regression. Deep learning is known for outstandingly accurate predictions on complex data but in regression tasks, it is predominantly used to just predict a single number. This ignores the non-deterministic character of most tasks. Especially if crucial decisions are based on the predictions, like in medical applications, it is essential to quantify the prediction uncertainty. The presented deep learning transformation model estimates the whole conditional probability distribution, which is the most thorough way to capture uncertainty about the outcome. We combine ideas from a statistical transformation model (most likely transformation) with recent transformation models from deep learning (normalizing flows) to predict complex outcome distributions. The core of the method is a parameterized transformation function which can be trained with the usual maximum likelihood framework using gradient descent. The method can be combined with existing deep learning architectures. For small machine learning benchmark datasets, we report state of the art performance for most dataset and partly even outperform it. Our method works for complex input data, which we demonstrate by employing a CNN architecture on image data.

Survival Forests under Test: Impact of the Proportional Hazards Assumption on Prognostic and Predictive Forests for ALS Survival

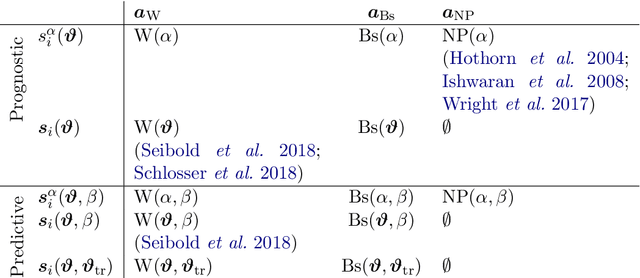
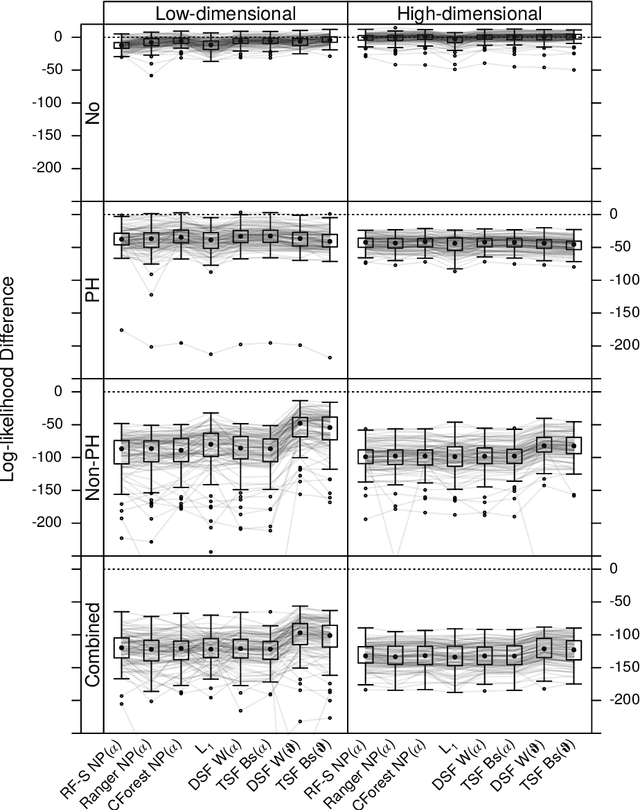
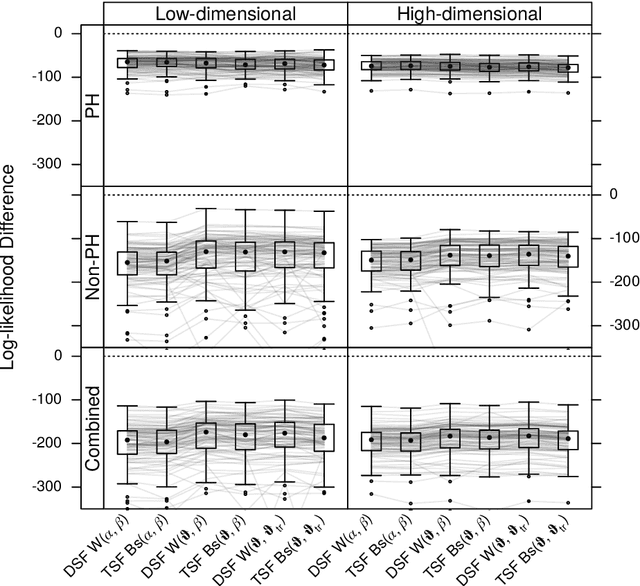
We investigate the effect of the proportional hazards assumption on prognostic and predictive models of the survival time of patients suffering from amyotrophic lateral sclerosis (ALS). We theoretically compare the underlying model formulations of several variants of survival forests and implementations thereof, including random forests for survival, conditional inference forests, Ranger, and survival forests with $L_1$ splitting, with two novel variants, namely distributional and transformation survival forests. Theoretical considerations explain the low power of log-rank-based splitting in detecting patterns in non-proportional hazards situations in survival trees and corresponding forests. This limitation can potentially be overcome by the alternative split procedures suggested herein. We empirically investigated this effect using simulation experiments and a re-analysis of the PRO-ACT database of ALS survival, giving special emphasis to both prognostic and predictive models.