How Inverse Conditional Flows Can Serve as a Substitute for Distributional Regression

Neural network representations of simple models, such as linear regression, are being studied increasingly to better understand the underlying principles of deep learning algorithms. However, neural representations of distributional regression models, such as the Cox model, have received little attention so far. We close this gap by proposing a framework for distributional regression using inverse flow transformations (DRIFT), which includes neural representations of the aforementioned models. We empirically demonstrate that the neural representations of models in DRIFT can serve as a substitute for their classical statistical counterparts in several applications involving continuous, ordered, time-series, and survival outcomes. We confirm that models in DRIFT empirically match the performance of several statistical methods in terms of estimation of partial effects, prediction, and aleatoric uncertainty quantification. DRIFT covers both interpretable statistical models and flexible neural networks opening up new avenues in both statistical modeling and deep learning.

Generalizing Orthogonalization for Models with Non-linearities

The complexity of black-box algorithms can lead to various challenges, including the introduction of biases. These biases present immediate risks in the algorithms' application. It was, for instance, shown that neural networks can deduce racial information solely from a patient's X-ray scan, a task beyond the capability of medical experts. If this fact is not known to the medical expert, automatic decision-making based on this algorithm could lead to prescribing a treatment (purely) based on racial information. While current methodologies allow for the "orthogonalization" or "normalization" of neural networks with respect to such information, existing approaches are grounded in linear models. Our paper advances the discourse by introducing corrections for non-linearities such as ReLU activations. Our approach also encompasses scalar and tensor-valued predictions, facilitating its integration into neural network architectures. Through extensive experiments, we validate our method's effectiveness in safeguarding sensitive data in generalized linear models, normalizing convolutional neural networks for metadata, and rectifying pre-existing embeddings for undesired attributes.

Model-based causal feature selection for general response types

Discovering causal relationships from observational data is a fundamental yet challenging task. In some applications, it may suffice to learn the causal features of a given response variable, instead of learning the entire underlying causal structure. Invariant causal prediction (ICP, Peters et al., 2016) is a method for causal feature selection which requires data from heterogeneous settings. ICP assumes that the mechanism for generating the response from its direct causes is the same in all settings and exploits this invariance to output a subset of the causal features. The framework of ICP has been extended to general additive noise models and to nonparametric settings using conditional independence testing. However, nonparametric conditional independence testing often suffers from low power (or poor type I error control) and the aforementioned parametric models are not suitable for applications in which the response is not measured on a continuous scale, but rather reflects categories or counts. To bridge this gap, we develop ICP in the context of transformation models (TRAMs), allowing for continuous, categorical, count-type, and uninformatively censored responses (we show that, in general, these model classes do not allow for identifiability when there is no exogenous heterogeneity). We propose TRAM-GCM, a test for invariance of a subset of covariates, based on the expected conditional covariance between environments and score residuals which satisfies uniform asymptotic level guarantees. For the special case of linear shift TRAMs, we propose an additional invariance test, TRAM-Wald, based on the Wald statistic. We implement both proposed methods in the open-source R package "tramicp" and show in simulations that under the correct model specification, our approach empirically yields higher power than nonparametric ICP based on conditional independence testing.

Deep conditional transformation models for survival analysis

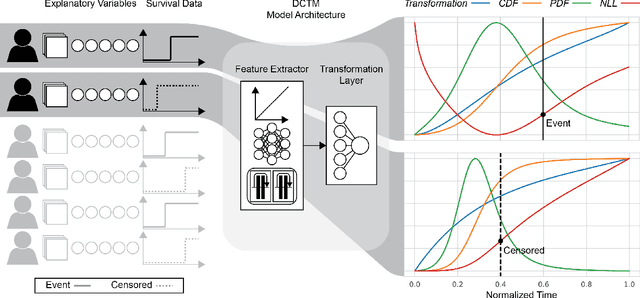
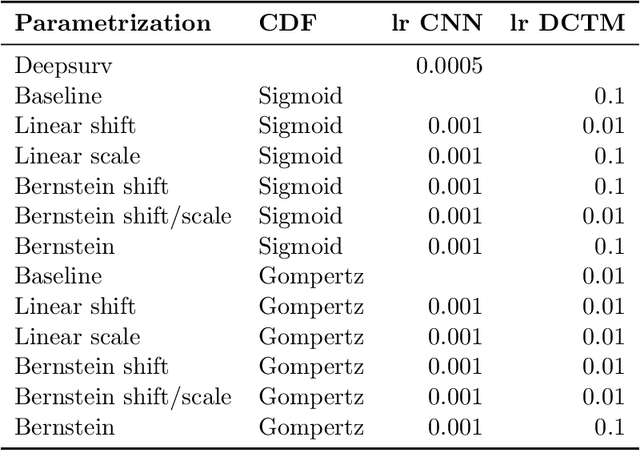
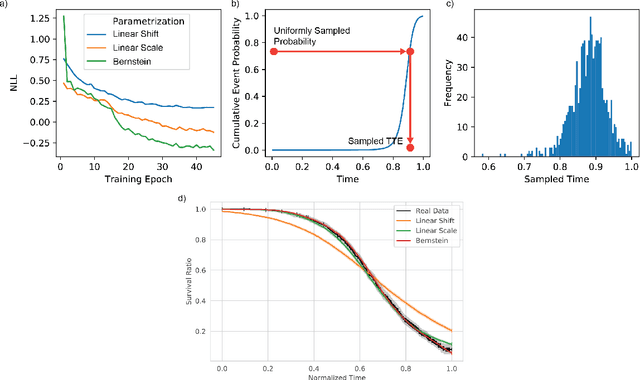
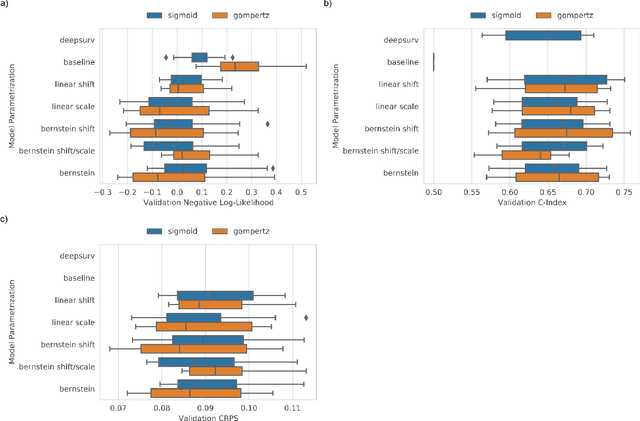
An every increasing number of clinical trials features a time-to-event outcome and records non-tabular patient data, such as magnetic resonance imaging or text data in the form of electronic health records. Recently, several neural-network based solutions have been proposed, some of which are binary classifiers. Parametric, distribution-free approaches which make full use of survival time and censoring status have not received much attention. We present deep conditional transformation models (DCTMs) for survival outcomes as a unifying approach to parametric and semiparametric survival analysis. DCTMs allow the specification of non-linear and non-proportional hazards for both tabular and non-tabular data and extend to all types of censoring and truncation. On real and semi-synthetic data, we show that DCTMs compete with state-of-the-art DL approaches to survival analysis.

Deep interpretable ensembles

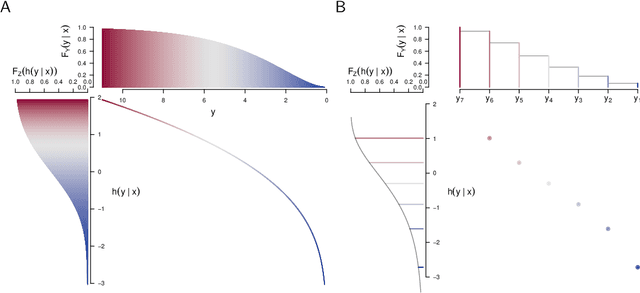
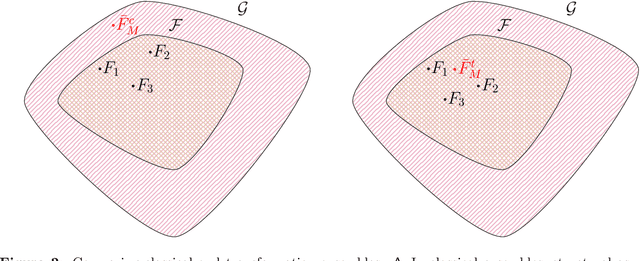
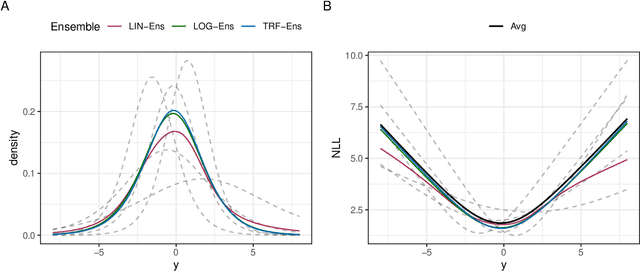
Ensembles improve prediction performance and allow uncertainty quantification by aggregating predictions from multiple models. In deep ensembling, the individual models are usually black box neural networks, or recently, partially interpretable semi-structured deep transformation models. However, interpretability of the ensemble members is generally lost upon aggregation. This is a crucial drawback of deep ensembles in high-stake decision fields, in which interpretable models are desired. We propose a novel transformation ensemble which aggregates probabilistic predictions with the guarantee to preserve interpretability and yield uniformly better predictions than the ensemble members on average. Transformation ensembles are tailored towards interpretable deep transformation models but are applicable to a wider range of probabilistic neural networks. In experiments on several publicly available data sets, we demonstrate that transformation ensembles perform on par with classical deep ensembles in terms of prediction performance, discrimination, and calibration. In addition, we demonstrate how transformation ensembles quantify both aleatoric and epistemic uncertainty, and produce minimax optimal predictions under certain conditions.

Ordinal Neural Network Transformation Models: Deep and interpretable regression models for ordinal outcomes

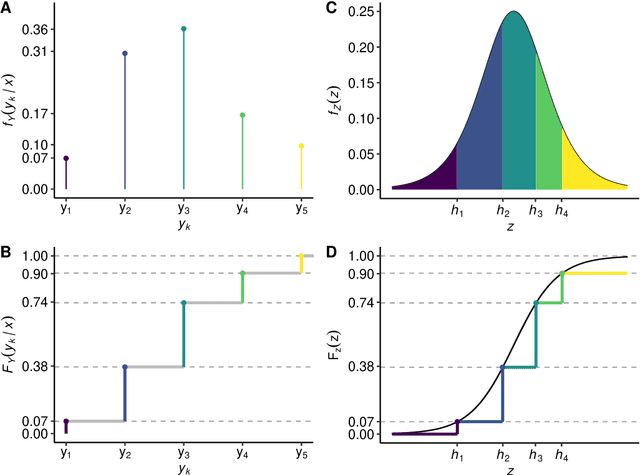
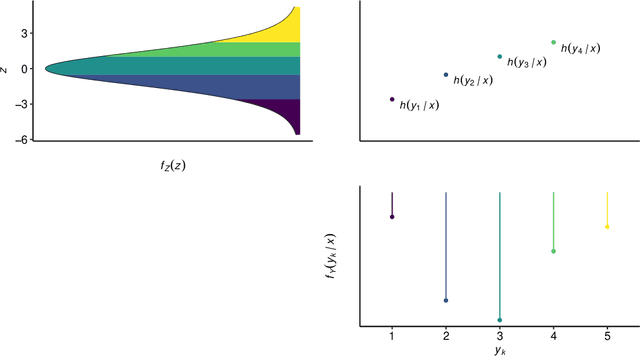
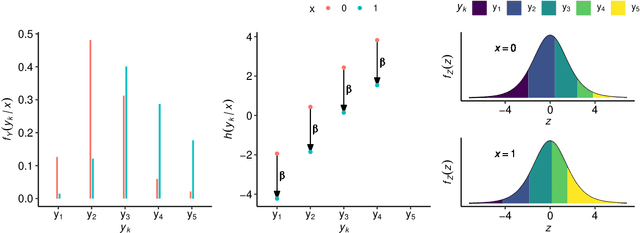
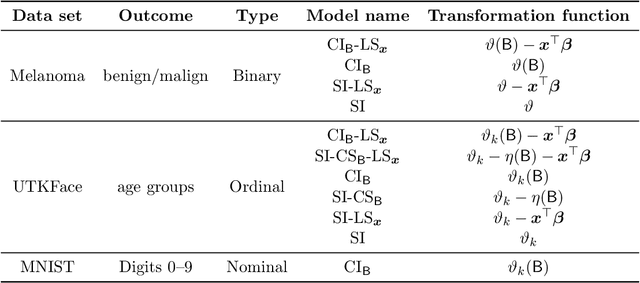
Outcomes with a natural order commonly occur in prediction tasks and oftentimes the available input data are a mixture of complex data, like images, and tabular predictors. Although deep Learning (DL) methods have shown outstanding performance on image classification, most models treat ordered outcomes as unordered and lack interpretability. In contrast, classical ordinal regression models yield interpretable predictor effects but are limited to tabular input data. Here, we present the highly modular class of ordinal neural network transformation models (ONTRAMs). Transformation models use a parametric transformation function and a simple distribution to trade off flexibility and interpretability of individual model components. In ONTRAMs, this trade-off is achieved by additively decomposing the transformation function into terms for the tabular and image data using a set of jointly trained neural networks. We show that the most flexible ONTRAMs achieve on-par performance with DL classifiers while outperforming them in training speed. We discuss how to interpret components of ONTRAMs in general and in the case of correlated tabular and image data. Taken together, ONTRAMs join benefits of DL and distributional regression to create interpretable prediction models for ordinal outcomes.