Deep Learning-based Approaches for State Space Models: A Selective Review

State-space models (SSMs) offer a powerful framework for dynamical system analysis, wherein the temporal dynamics of the system are assumed to be captured through the evolution of the latent states, which govern the values of the observations. This paper provides a selective review of recent advancements in deep neural network-based approaches for SSMs, and presents a unified perspective for discrete time deep state space models and continuous time ones such as latent neural Ordinary Differential and Stochastic Differential Equations. It starts with an overview of the classical maximum likelihood based approach for learning SSMs, reviews variational autoencoder as a general learning pipeline for neural network-based approaches in the presence of latent variables, and discusses in detail representative deep learning models that fall under the SSM framework. Very recent developments, where SSMs are used as standalone architectural modules for improving efficiency in sequence modeling, are also examined. Finally, examples involving mixed frequency and irregularly-spaced time series data are presented to demonstrate the advantage of SSMs in these settings.

A VAE-based Framework for Learning Multi-Level Neural Granger-Causal Connectivity

Granger causality has been widely used in various application domains to capture lead-lag relationships amongst the components of complex dynamical systems, and the focus in extant literature has been on a single dynamical system. In certain applications in macroeconomics and neuroscience, one has access to data from a collection of related such systems, wherein the modeling task of interest is to extract the shared common structure that is embedded across them, as well as to identify the idiosyncrasies within individual ones. This paper introduces a Variational Autoencoder (VAE) based framework that jointly learns Granger-causal relationships amongst components in a collection of related-yet-heterogeneous dynamical systems, and handles the aforementioned task in a principled way. The performance of the proposed framework is evaluated on several synthetic data settings and benchmarked against existing approaches designed for individual system learning. The method is further illustrated on a real dataset involving time series data from a neurophysiological experiment and produces interpretable results.

A Penalty Based Method for Communication-Efficient Decentralized Bilevel Programming

Bilevel programming has recently received attention in the literature, due to a wide range of applications, including reinforcement learning and hyper-parameter optimization. However, it is widely assumed that the underlying bilevel optimization problem is solved either by a single machine or in the case of multiple machines connected in a star-shaped network, i.e., federated learning setting. The latter approach suffers from a high communication cost on the central node (e.g., parameter server) and exhibits privacy vulnerabilities. Hence, it is of interest to develop methods that solve bilevel optimization problems in a communication-efficient decentralized manner. To that end, this paper introduces a penalty function based decentralized algorithm with theoretical guarantees for this class of optimization problems. Specifically, a distributed alternating gradient-type algorithm for solving consensus bilevel programming over a decentralized network is developed. A key feature of the proposed algorithm is to estimate the hyper-gradient of the penalty function via decentralized computation of matrix-vector products and few vector communications, which is then integrated within our alternating algorithm to give the finite-time convergence analysis under different convexity assumptions. Owing to the generality of this complexity analysis, our result yields convergence rates for a wide variety of consensus problems including minimax and compositional optimization. Empirical results on both synthetic and real datasets demonstrate that the proposed method works well in practice.

Explaining the root causes of unit-level changes

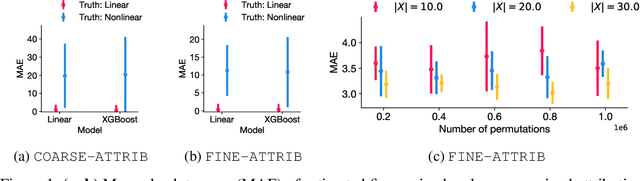
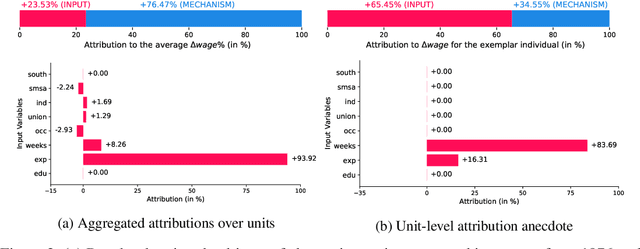
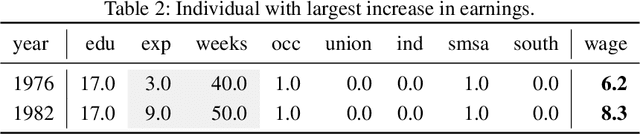
Existing methods of explainable AI and interpretable ML cannot explain change in the values of an output variable for a statistical unit in terms of the change in the input values and the change in the "mechanism" (the function transforming input to output). We propose two methods based on counterfactuals for explaining unit-level changes at various input granularities using the concept of Shapley values from game theory. These methods satisfy two key axioms desirable for any unit-level change attribution method. Through simulations, we study the reliability and the scalability of the proposed methods. We get sensible results from a case study on identifying the drivers of the change in the earnings for individuals in the US.

A Coupled CP Decomposition for Principal Components Analysis of Symmetric Networks

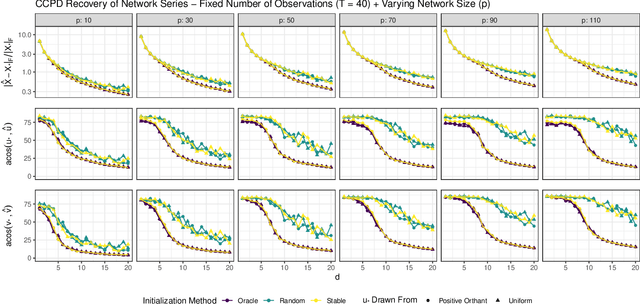
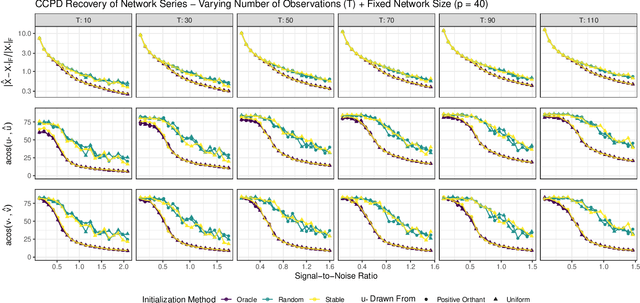
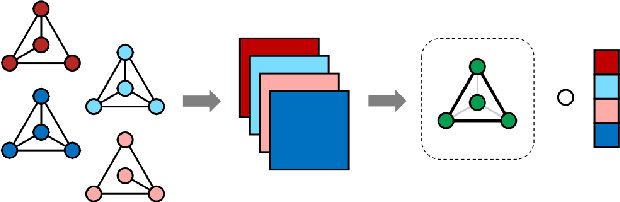
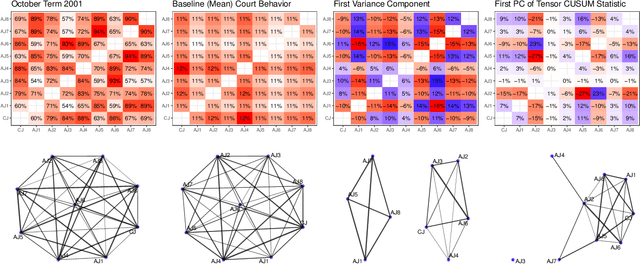
In a number of application domains, one observes a sequence of network data; for example, repeated measurements between users interactions in social media platforms, financial correlation networks over time, or across subjects, as in multi-subject studies of brain connectivity. One way to analyze such data is by stacking networks into a third-order array or tensor. We propose a principal components analysis (PCA) framework for sequence network data, based on a novel decomposition for semi-symmetric tensors. We derive efficient algorithms for computing our proposed "Coupled CP" decomposition and establish estimation consistency of our approach under an analogue of the spiked covariance model with rates the same as the matrix case up to a logarithmic term. Our framework inherits many of the strengths of classical PCA and is suitable for a wide range of unsupervised learning tasks, including identifying principal networks, isolating meaningful changepoints or outliers across observations, and for characterizing the "variability network" of the most varying edges. Finally, we demonstrate the effectiveness of our proposal on simulated data and on examples from political science and financial economics. The proof techniques used to establish our main consistency results are surprisingly straight-forward and may find use in a variety of other matrix and tensor decomposition problems.

Joint Learning of Linear Time-Invariant Dynamical Systems

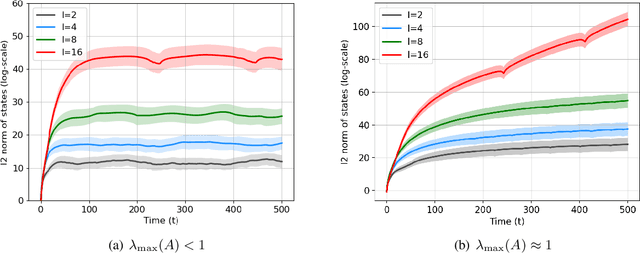
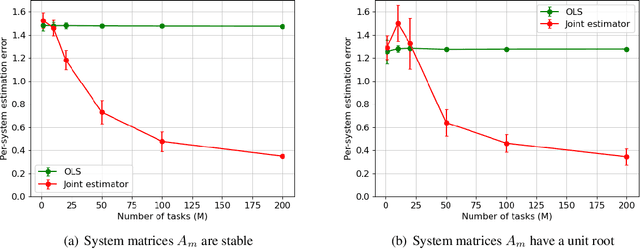
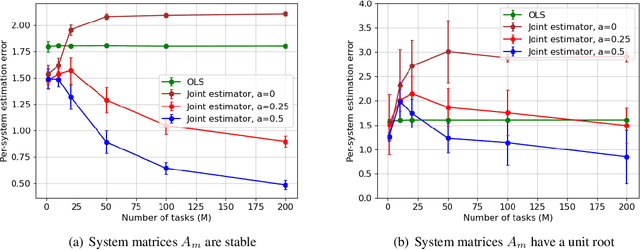
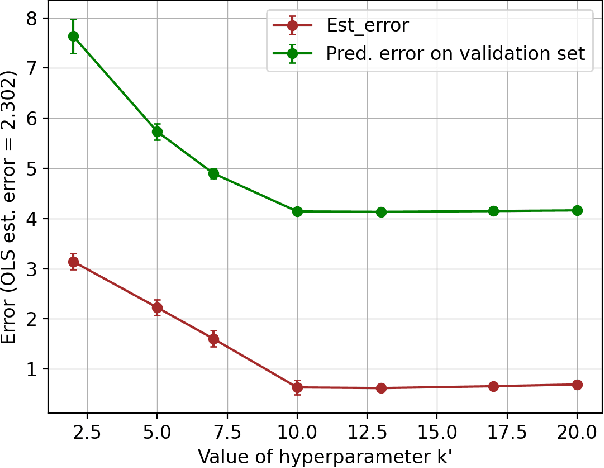
Learning the parameters of a linear time-invariant dynamical system (LTIDS) is a problem of current interest. In many applications, one is interested in jointly learning the parameters of multiple related LTIDS, which remains unexplored to date. To that end, we develop a joint estimator for learning the transition matrices of LTIDS that share common basis matrices. Further, we establish finite-time error bounds that depend on the underlying sample size, dimension, number of tasks, and spectral properties of the transition matrices. The results are obtained under mild regularity assumptions and showcase the gains from pooling information across LTIDS, in comparison to learning each system separately. We also study the impact of misspecifying the joint structure of the transition matrices and show that the established results are robust in the presence of moderate misspecifications.

Inference for Change Points in High Dimensional Mean Shift Models

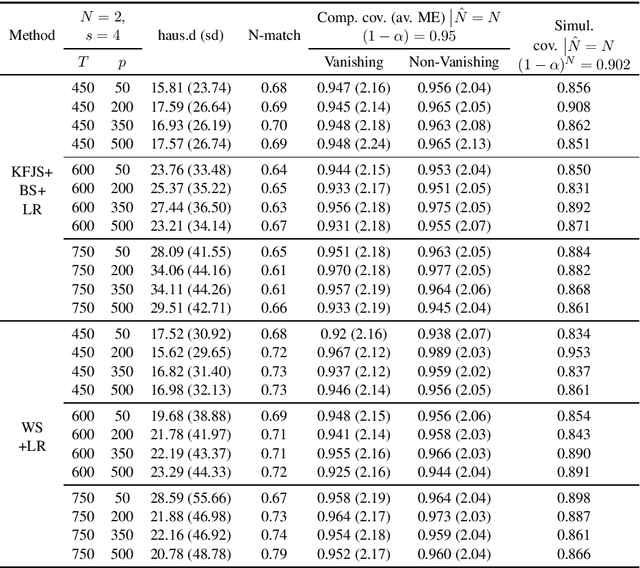
We consider the problem of constructing confidence intervals for the locations of change points in a high-dimensional mean shift model. To that end, we develop a locally refitted least squares estimator and obtain component-wise and simultaneous rates of estimation of the underlying change points. The simultaneous rate is the sharpest available in the literature by at least a factor of $\log p,$ while the component-wise one is optimal. These results enable existence of limiting distributions. Component-wise distributions are characterized under both vanishing and non-vanishing jump size regimes, while joint distributions for any finite subset of change point estimates are characterized under the latter regime, which also yields asymptotic independence of these estimates. The combined results are used to construct asymptotically valid component-wise and simultaneous confidence intervals for the change point parameters. The results are established under a high dimensional scaling, allowing for diminishing jump sizes, in the presence of diverging number of change points and under subexponential errors. They are illustrated on synthetic data and on sensor measurements from smartphones for activity recognition.

A Decentralized Adaptive Momentum Method for Solving a Class of Min-Max Optimization Problems

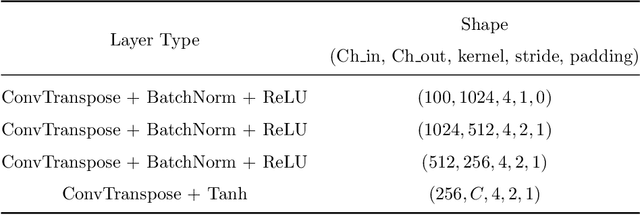
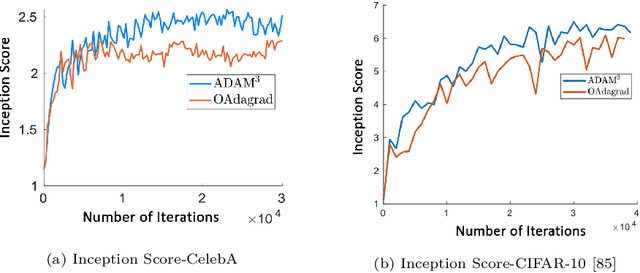
Min-max saddle point games have recently been intensely studied, due to their wide range of applications, including training Generative Adversarial Networks (GANs). However, most of the recent efforts for solving them are limited to special regimes such as convex-concave games. Further, it is customarily assumed that the underlying optimization problem is solved either by a single machine or in the case of multiple machines connected in centralized fashion, wherein each one communicates with a central node. The latter approach becomes challenging, when the underlying communications network has low bandwidth. In addition, privacy considerations may dictate that certain nodes can communicate with a subset of other nodes. Hence, it is of interest to develop methods that solve min-max games in a decentralized manner. To that end, we develop a decentralized adaptive momentum (ADAM)-type algorithm for solving min-max optimization problem under the condition that the objective function satisfies a Minty Variational Inequality condition, which is a generalization to convex-concave case. The proposed method overcomes shortcomings of recent non-adaptive gradient-based decentralized algorithms for min-max optimization problems that do not perform well in practice and require careful tuning. In this paper, we obtain non-asymptotic rates of convergence of the proposed algorithm (coined DADAM$^3$) for finding a (stochastic) first-order Nash equilibrium point and subsequently evaluate its performance on training GANs. The extensive empirical evaluation shows that DADAM$^3$ outperforms recently developed methods, including decentralized optimistic stochastic gradient for solving such min-max problems.

Solving a class of non-convex min-max games using adaptive momentum methods

Adaptive momentum methods have recently attracted a lot of attention for training of deep neural networks. They use an exponential moving average of past gradients of the objective function to update both search directions and learning rates. However, these methods are not suited for solving min-max optimization problems that arise in training generative adversarial networks. In this paper, we propose an adaptive momentum min-max algorithm that generalizes adaptive momentum methods to the non-convex min-max regime. Further, we establish non-asymptotic rates of convergence for the proposed algorithm when used in a reasonably broad class of non-convex min-max optimization problems. Experimental results illustrate its superior performance vis-a-vis benchmark methods for solving such problems.

Sparse Partial Least Squares for Coarse Noisy Graph Alignment

Graph signal processing (GSP) provides a powerful framework for analyzing signals arising in a variety of domains. In many applications of GSP, multiple network structures are available, each of which captures different aspects of the same underlying phenomenon. To integrate these different data sources, graph alignment techniques attempt to find the best correspondence between vertices of two graphs. We consider a generalization of this problem, where there is no natural one-to-one mapping between vertices, but where there is correspondence between the community structures of each graph. Because we seek to learn structure at this higher community level, we refer to this problem as "coarse" graph alignment. To this end, we propose a novel regularized partial least squares method which both incorporates the observed graph structures and imposes sparsity in order to reflect the underlying block community structure. We provide efficient algorithms for our method and demonstrate its effectiveness in simulations.