Enhanced graph-learning schemes driven by similar distributions of motifs
Paper and Code
Jul 11, 2022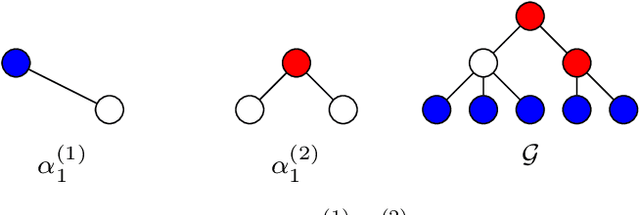
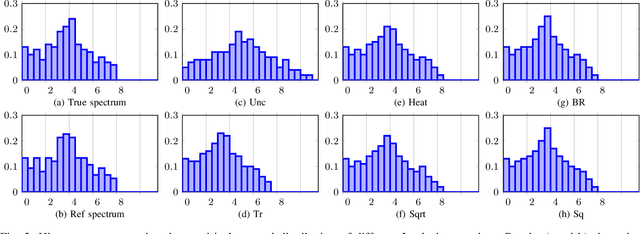
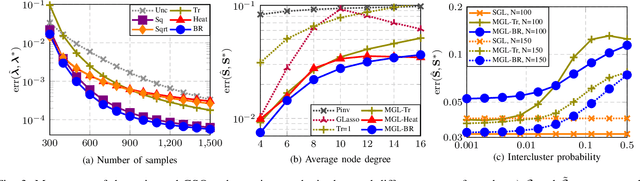
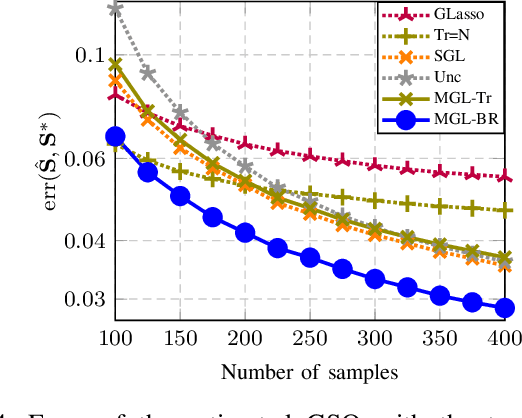
This paper looks at the task of network topology inference, where the goal is to learn an unknown graph from nodal observations. One of the novelties of the approach put forth is the consideration of prior information about the density of motifs of the unknown graph to enhance the inference of classical Gaussian graphical models. Dealing with the density of motifs directly constitutes a challenging combinatorial task. However, we note that if two graphs have similar motif densities, one can show that the expected value of a polynomial applied to their empirical spectral distributions will be similar. Guided by this, we first assume that we have a reference graph that is related to the sought graph (in the sense of having similar motif densities) and then, we exploit this relation by incorporating a similarity constraint and a regularization term in the network topology inference optimization problem. The (non-)convexity of the optimization problem is discussed and a computational efficient alternating majorization-minimization algorithm is designed. We assess the performance of the proposed method through exhaustive numerical experiments where different constraints are considered and compared against popular baselines algorithms on both synthetic and real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge