The Persistent Robot Charging Problem for Long-Duration Autonomy

This paper introduces a novel formulation aimed at determining the optimal schedule for recharging a fleet of $n$ heterogeneous robots, with the primary objective of minimizing resource utilization. This study provides a foundational framework applicable to Multi-Robot Mission Planning, particularly in scenarios demanding Long-Duration Autonomy (LDA) or other contexts that necessitate periodic recharging of multiple robots. A novel Integer Linear Programming (ILP) model is proposed to calculate the optimal initial conditions (partial charge) for individual robots, leading to the minimal utilization of charging stations. This formulation was further generalized to maximize the servicing time for robots given adequate charging stations. The efficacy of the proposed formulation is evaluated through a comparative analysis, measuring its performance against the thrift price scheduling algorithm documented in the existing literature. The findings not only validate the effectiveness of the proposed approach but also underscore its potential as a valuable tool in optimizing resource allocation for a range of robotic and engineering applications.

Assisted Path Planning for a UGV-UAV Team Through a Stochastic Network

In this article, we consider a multi-agent path planning problem in a stochastic environment. The environment, which can be an urban road network, is represented by a graph where the travel time for selected road segments (impeded edges) is a random variable because of traffic congestion. An unmanned ground vehicle (UGV) wishes to travel from a starting location to a destination while minimizing the arrival time at the destination. UGV can traverse through an impeded edge but the true travel time is only realized at the end of that edge. This implies that the UGV can potentially get stuck in an impeded edge with high travel time. A support vehicle, such as an unmanned aerial vehicle (UAV) is simultaneously deployed from its starting position to assist the UGV by inspecting and realizing the true cost of impeded edges. With the updated information from UAV, UGV can efficiently reroute its path to the destination. The UGV does not wait at any time until it reaches the destination. The UAV is permitted to terminate its path at any vertex. The goal is then to develop an online algorithm to determine efficient paths for the UGV and the UAV based on the current information so that the UGV reaches the destination in minimum time. We refer to this problem as Stochastic Assisted Path Planning (SAPP). We present Dynamic $k$-Shortest Path Planning (D*KSPP) algorithm for the UGV planning and Rural Postman Problem (RPP) formulation for the UAV planning. Due to the scalability challenges of RPP, we also present a heuristic based Priority Assignment Algorithm (PAA) for the UAV planning. Computational results are presented to corroborate the effectiveness of the proposed algorithm to solve SAPP.

The Weighted Markov-Dubins Problem

In this article, a variation of the classical Markov-Dubins problem is considered, which deals with curvature-constrained least-cost paths in a plane with prescribed initial and final configurations, different bounds for the sinistral and dextral curvatures, and penalties $\mu_L$ and $\mu_R$ for the sinistral and dextral turns, respectively. The addressed problem generalizes the classical Markov-Dubins problem and the asymmetric sinistral/dextral Markov-Dubins problem. The proposed formulation can be used to model an Unmanned Aerial Vehicle (UAV) with a penalty associated with a turn due to a loss in altitude while turning or a UAV with different costs for the sinistral and dextral turns due to hardware failures or environmental conditions. Using optimal control theory, the main result of this paper shows that the optimal path belongs to a set of at most $21$ candidate paths, each comprising of at most five segments. Unlike in the classical Markov-Dubins problem, the $CCC$ path, which is a candidate path for the classical Markov-Dubins problem, is not optimal for the weighted Markov-Dubins problem. Moreover, the obtained list of candidate paths for the weighted Markov-Dubins problem reduces to the standard $CSC$ and $CCC$ paths and the corresponding degenerate paths when $\mu_L$ and $\mu_R$ approach zero.

Cooperative Coverage with a Leader and a Wingmate in Communication-Constrained Environments

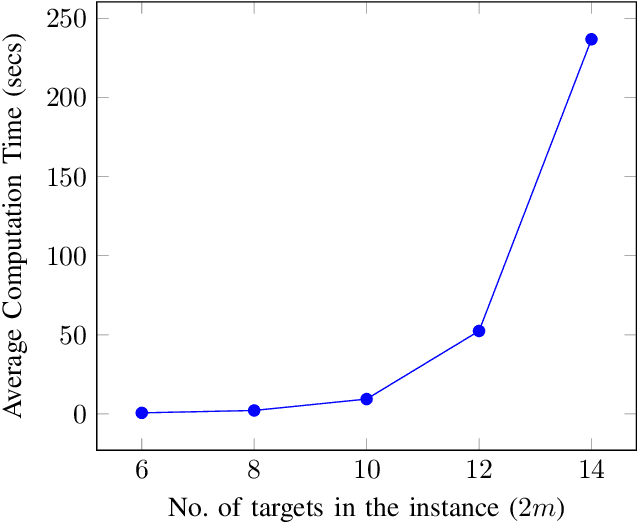
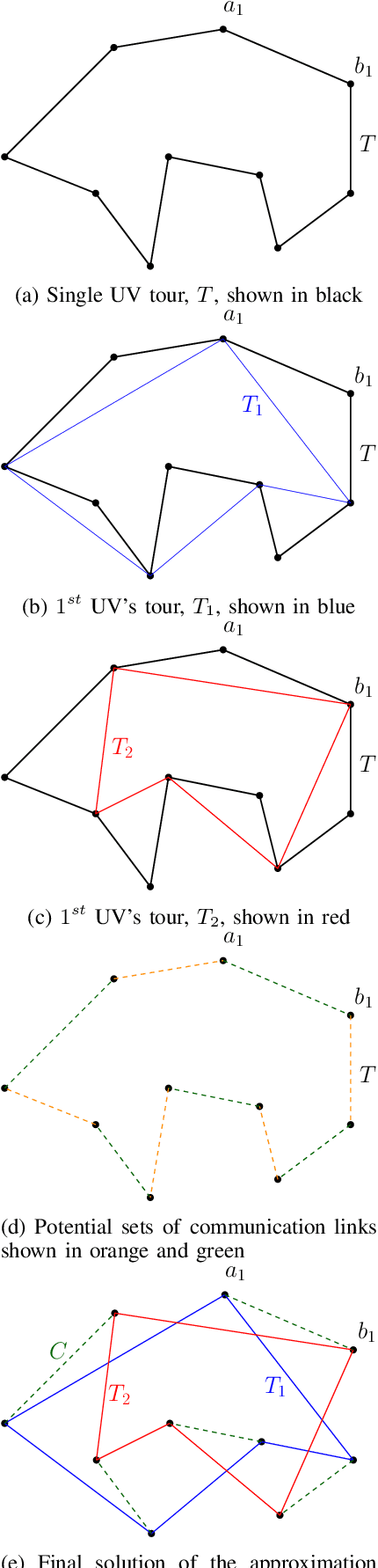
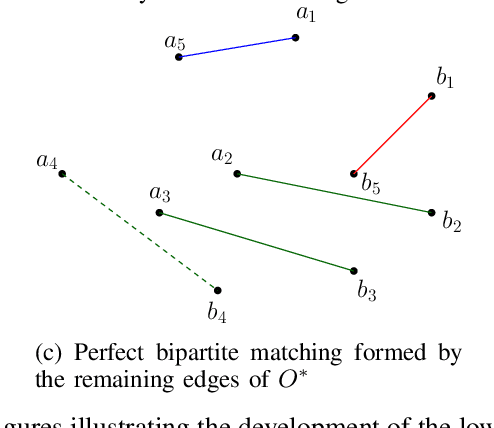
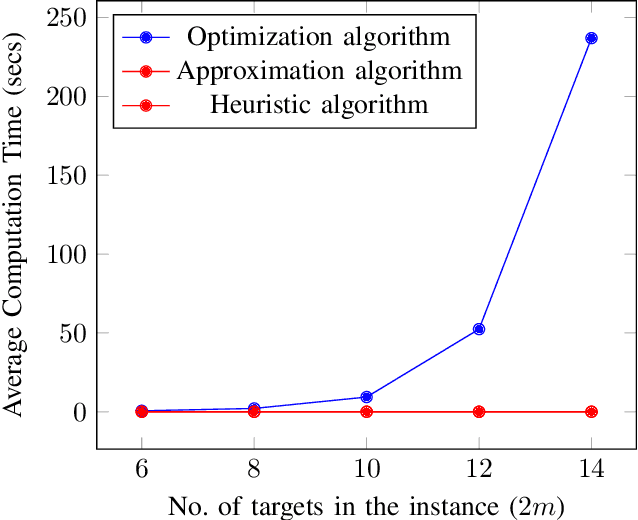
We consider a mission framework in which two unmanned vehicles (UVs), a leader and a wingmate, are required to provide cooperative coverage of an environment while being within a short communication range. This framework finds applications in underwater and/or military domains, where certain constraints are imposed on communication by either the application or the environment. An important objective of missions within this framework is to minimize the total travel and communication costs of the leader-wingmate duo. In this paper, we propose and formulate the problem of finding routes for the UVs that minimize the sum of their travel and communication costs as a network optimization problem of the form of a binary program (BP). The BP is computationally expensive, with the time required to compute optimal solutions increasing rapidly with the problem size. To address this challenge, here, we propose two algorithms, an approximation algorithm and a heuristic algorithm, to solve large-scale instances of the problem swiftly. We demonstrate the effectiveness and the scalability of these algorithms through an analysis of extensive numerical simulations performed over 500 instances, with the number of targets in the instances ranging from 6 to 100.

Assisted Shortest Path Planning for a Convoy through a Repairable Network

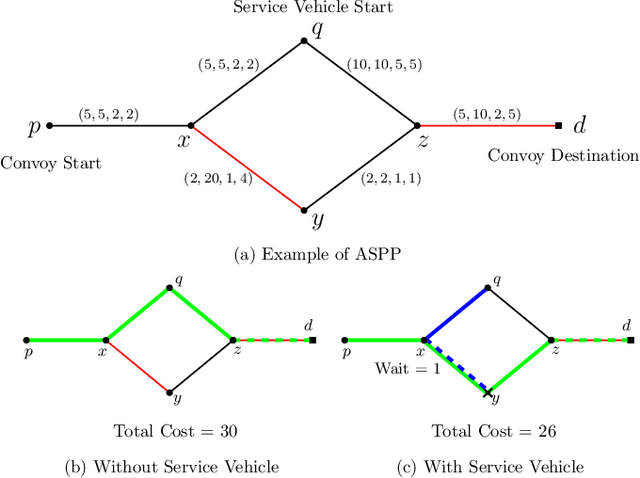
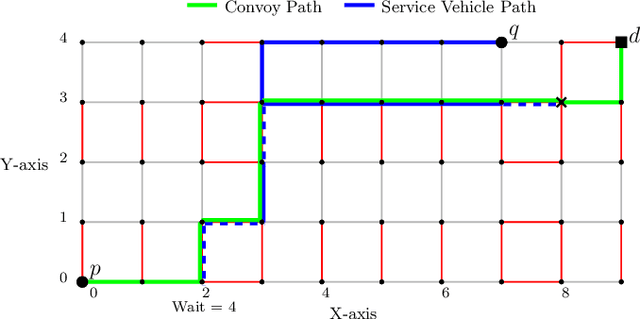
In this article, we consider a multi-agent path planning problem in a partially impeded environment. The impeded environment is represented by a graph with select road segments (edges) in disrepair impeding vehicular movement in the road network. A convoy wishes to travel from a starting location to a destination while minimizing some accumulated cost. The convoy may traverse an impeded edge for an additional cost (associated with repairing the edge) than if it were unimpeded. A second vehicle, referred to as a service vehicle, is simultaneously deployed with the convoy. The service vehicle assists the convoy by repairing an edge, reducing the cost for the convoy to traverse that edge. The convoy is permitted to wait at any vertex to allow the service vehicle to complete repairing an edge. The service vehicle is permitted to terminate its path at any vertex. The goal is then to find a pair of paths so the convoy reaches its destination while minimizing the total time (cost) the two vehicles are active, including any time the convoy waits. We refer to this problem as the Assisted Shortest Path Problem (ASPP). We present a generalized permanent labeling algorithm to find an optimal solution for the ASPP. We also introduce additional modifications to the labeling algorithm to significantly improve the computation time and refer to the modified labeling algorithm as $GPLA^*$. Computational results are presented to illustrate the effectiveness of $GPLA^*$ in solving the ASPP. We then give concluding remarks and briefly discuss potential variants of the ASPP for future work.

Bounds on Optimal Revisit Times in Persistent Monitoring Missions with a Distinct \& Remote Service Station

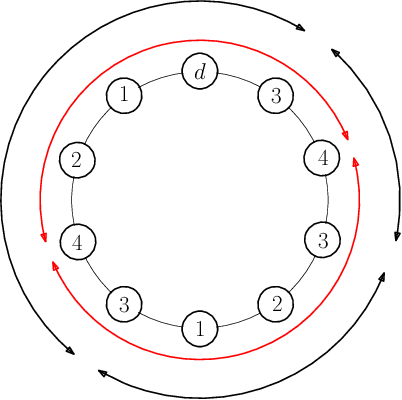
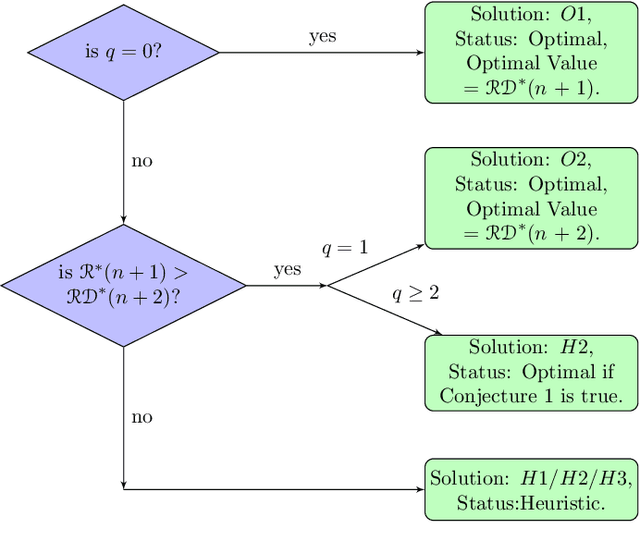
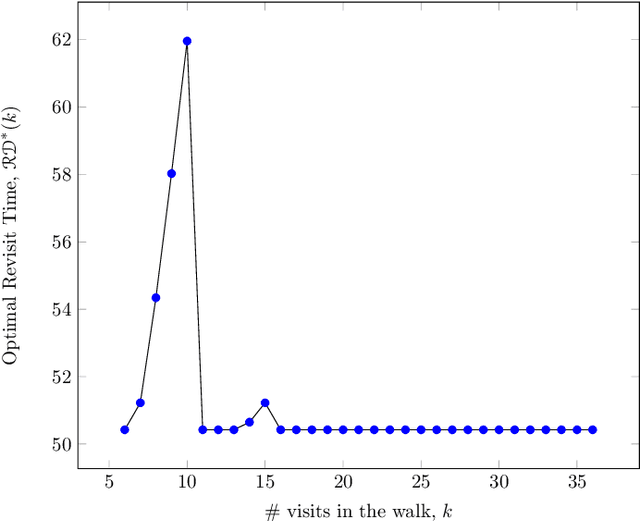
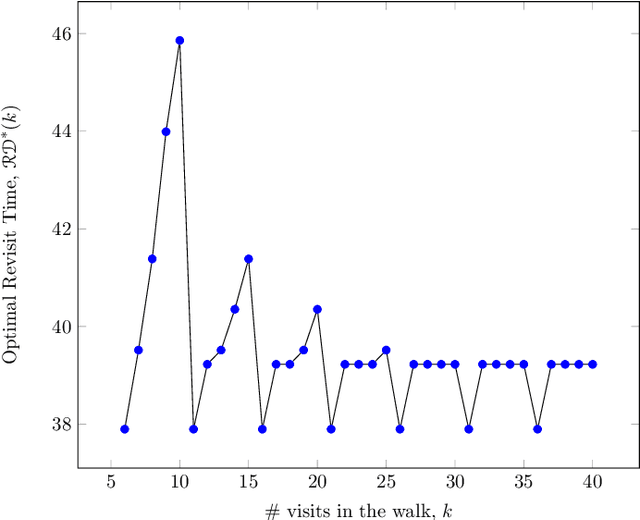
Persistent monitoring missions require an up-to-date knowledge of the changing state of the underlying environment. UAVs can be gainfully employed to continually visit a set of targets representing tasks (and locations) in the environment and collect data therein for long time periods. The enduring nature of these missions requires the UAV to be regularly recharged at a service station. In this paper, we consider the case in which the service station is not co-located with any of the targets. An efficient monitoring requires the revisit time, defined as the maximum of the time elapsed between successive revisits to targets, to be minimized. Here, we consider the problem of determining UAV routes that lead to the minimum revisit time. The problem is NP-hard, and its computational difficulty increases with the fuel capacity of the UAV. We develop an algorithm to construct near-optimal solutions to the problem quickly, when the fuel capacity exceeds a threshold. We also develop lower bounds to the optimal revisit time and use these bounds to demonstrate (through numerical simulations) that the constructed solutions are, on an average, at most 0.01% away from the optimum.

Persistent Monitoring of Dynamically Changing Environments Using an Unmanned Vehicle

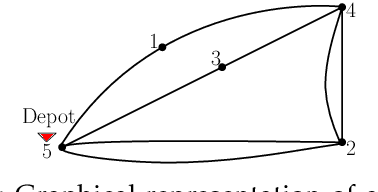
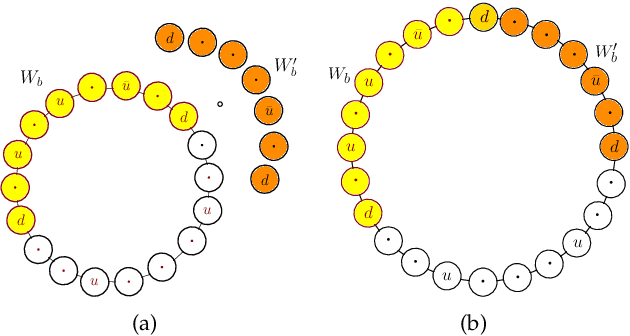
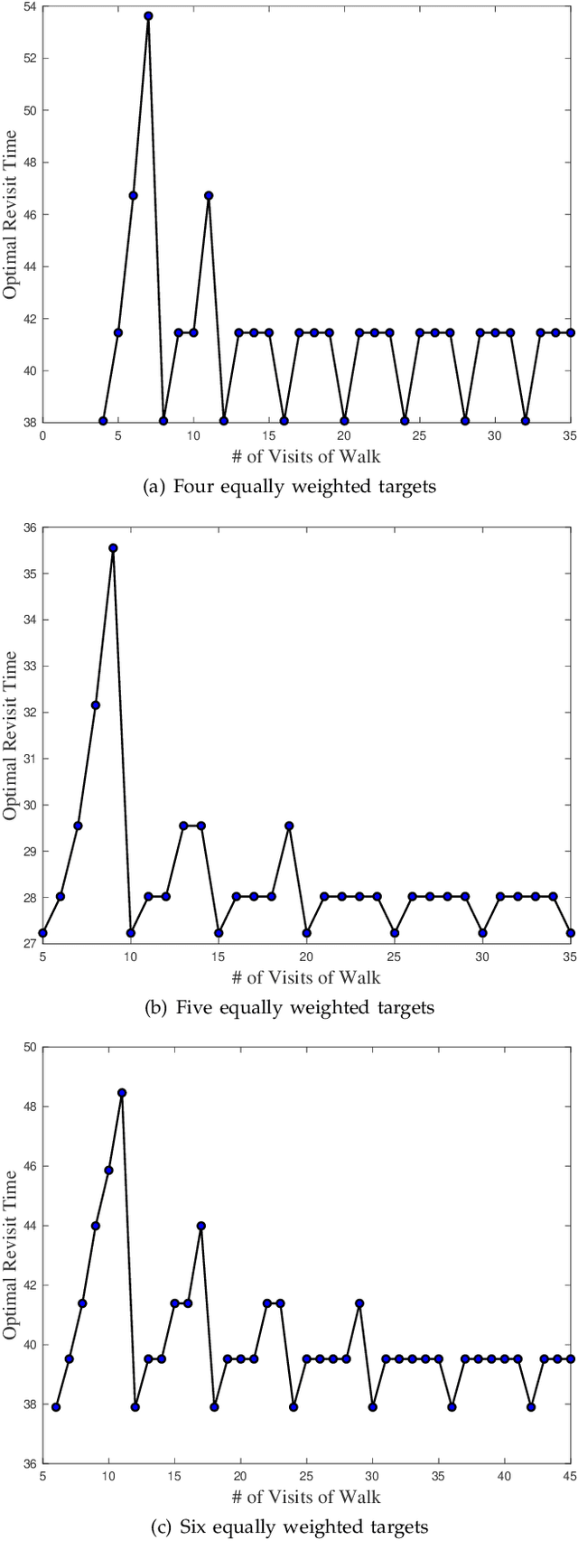
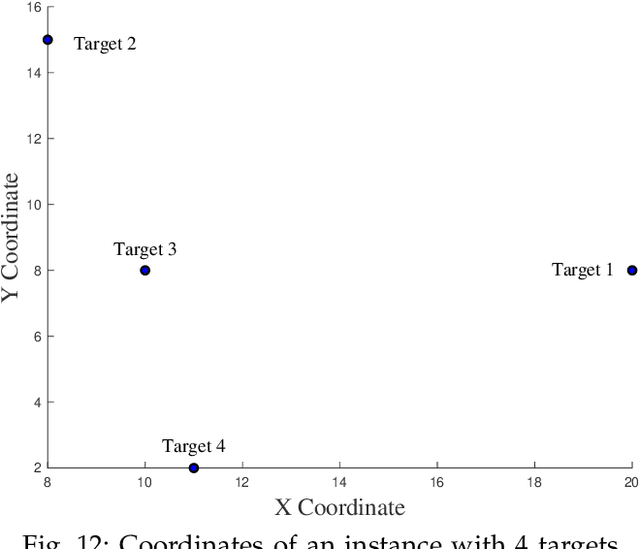
We consider the problem of planning a closed walk $\mathcal W$ for a UAV to persistently monitor a finite number of stationary targets with equal priorities and dynamically changing properties. A UAV must physically visit the targets in order to monitor them and collect information therein. The frequency of monitoring any given target is specified by a target revisit time, $i.e.$, the maximum allowable time between any two successive visits to the target. The problem considered in this paper is the following: Given $n$ targets and $k \geq n$ allowed visits to them, find an optimal closed walk $\mathcal W^*(k)$ so that every target is visited at least once and the maximum revisit time over all the targets, $\mathcal R(\mathcal W(k))$, is minimized. We prove the following: If $k \geq n^2-n$, $\mathcal R(\mathcal W^*(k))$ (or simply, $\mathcal R^*(k)$) takes only two values: $\mathcal R^*(n)$ when $k$ is an integral multiple of $n$, and $\mathcal R^*(n+1)$ otherwise. This result suggests significant computational savings - one only needs to determine $\mathcal W^*(n)$ and $\mathcal W^*(n+1)$ to construct an optimal solution $\mathcal W^*(k)$. We provide MILP formulations for computing $\mathcal W^*(n)$ and $\mathcal W^*(n+1)$. Furthermore, for {\it any} given $k$, we prove that $\mathcal R^*(k) \geq \mathcal R^*(k+n)$.