Cooperative Coverage with a Leader and a Wingmate in Communication-Constrained Environments

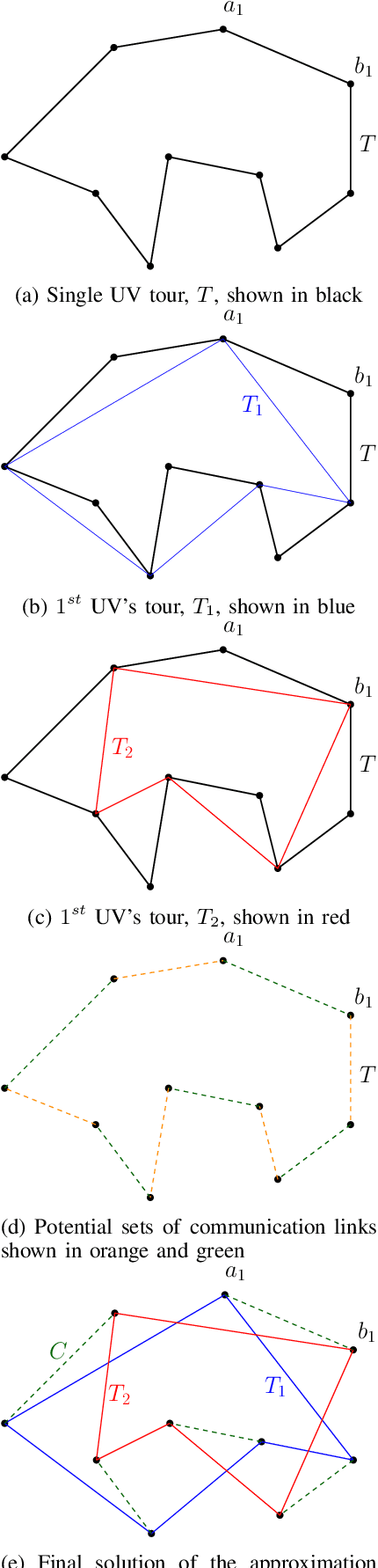
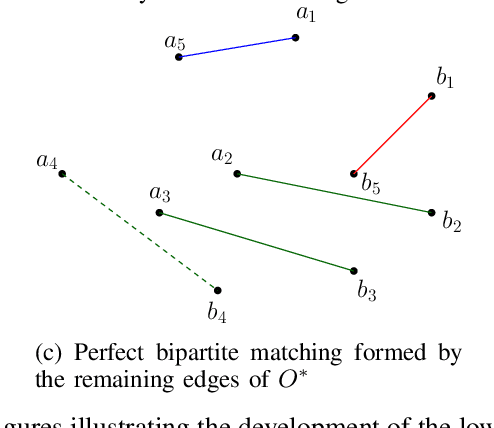
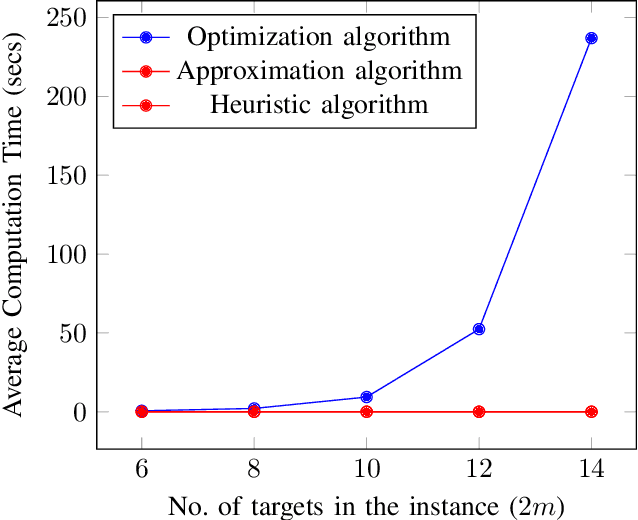
We consider a mission framework in which two unmanned vehicles (UVs), a leader and a wingmate, are required to provide cooperative coverage of an environment while being within a short communication range. This framework finds applications in underwater and/or military domains, where certain constraints are imposed on communication by either the application or the environment. An important objective of missions within this framework is to minimize the total travel and communication costs of the leader-wingmate duo. In this paper, we propose and formulate the problem of finding routes for the UVs that minimize the sum of their travel and communication costs as a network optimization problem of the form of a binary program (BP). The BP is computationally expensive, with the time required to compute optimal solutions increasing rapidly with the problem size. To address this challenge, here, we propose two algorithms, an approximation algorithm and a heuristic algorithm, to solve large-scale instances of the problem swiftly. We demonstrate the effectiveness and the scalability of these algorithms through an analysis of extensive numerical simulations performed over 500 instances, with the number of targets in the instances ranging from 6 to 100.

Bounds on Optimal Revisit Times in Persistent Monitoring Missions with a Distinct \& Remote Service Station

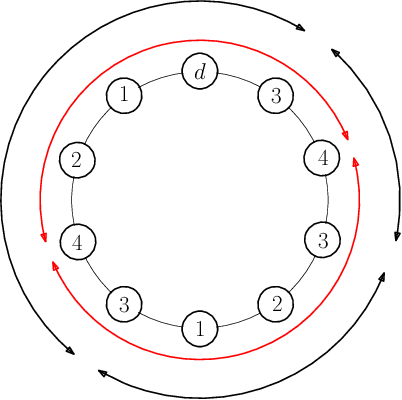
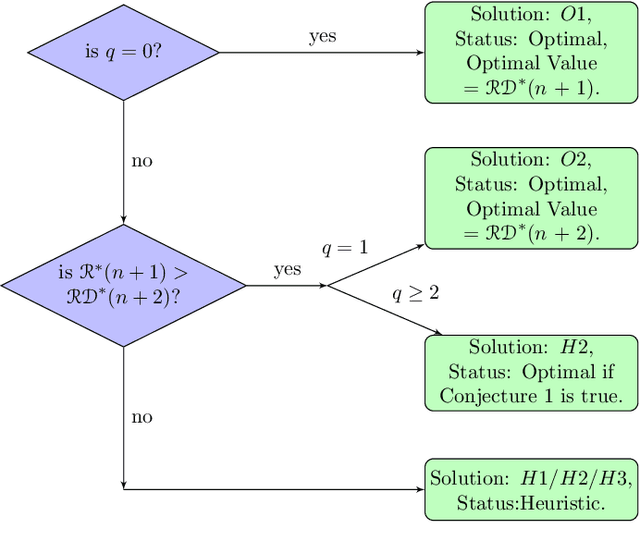
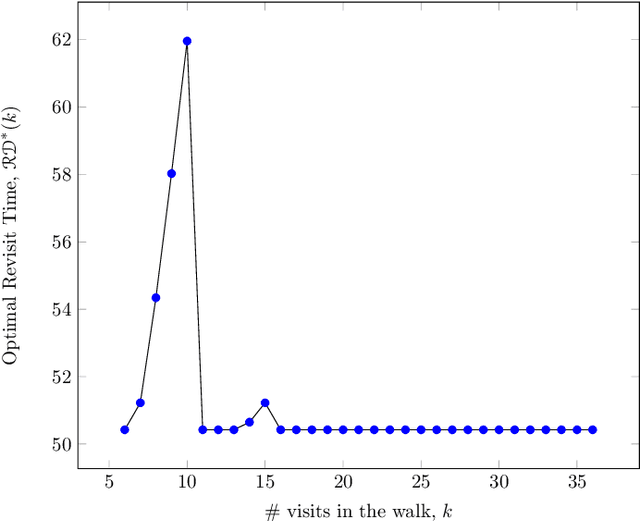
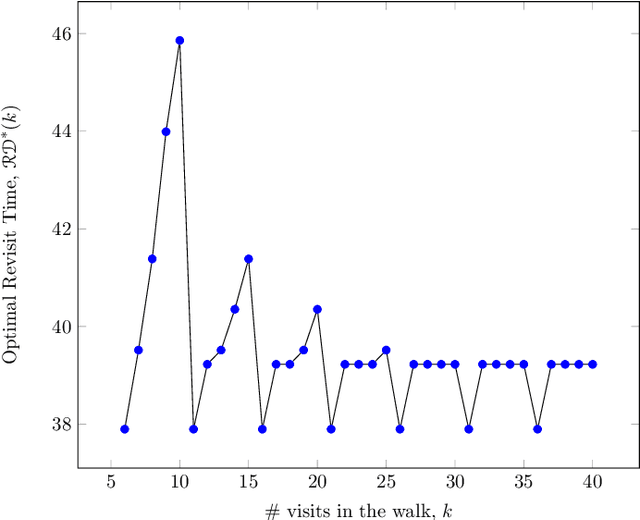
Persistent monitoring missions require an up-to-date knowledge of the changing state of the underlying environment. UAVs can be gainfully employed to continually visit a set of targets representing tasks (and locations) in the environment and collect data therein for long time periods. The enduring nature of these missions requires the UAV to be regularly recharged at a service station. In this paper, we consider the case in which the service station is not co-located with any of the targets. An efficient monitoring requires the revisit time, defined as the maximum of the time elapsed between successive revisits to targets, to be minimized. Here, we consider the problem of determining UAV routes that lead to the minimum revisit time. The problem is NP-hard, and its computational difficulty increases with the fuel capacity of the UAV. We develop an algorithm to construct near-optimal solutions to the problem quickly, when the fuel capacity exceeds a threshold. We also develop lower bounds to the optimal revisit time and use these bounds to demonstrate (through numerical simulations) that the constructed solutions are, on an average, at most 0.01% away from the optimum.

Persistent Monitoring of Dynamically Changing Environments Using an Unmanned Vehicle

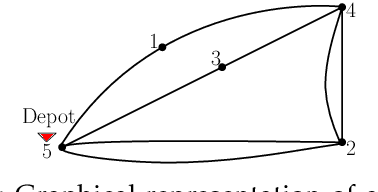
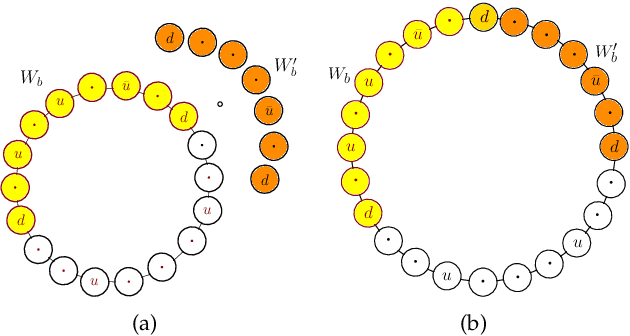
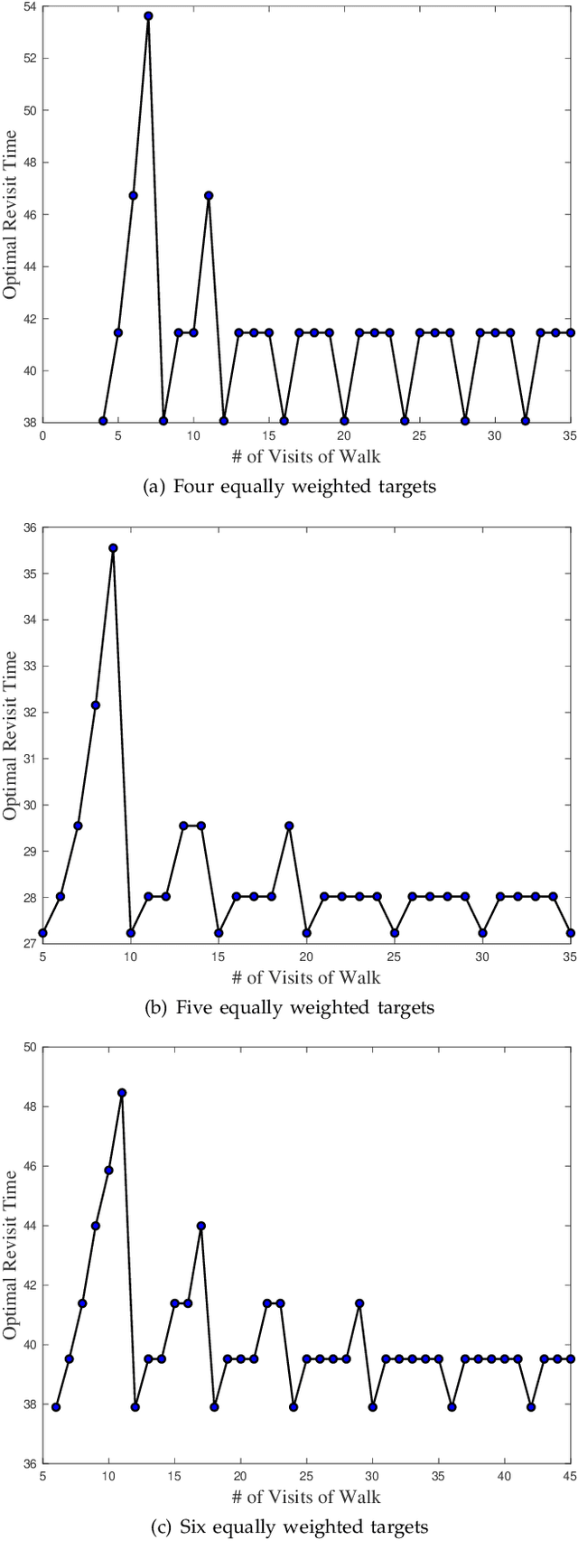
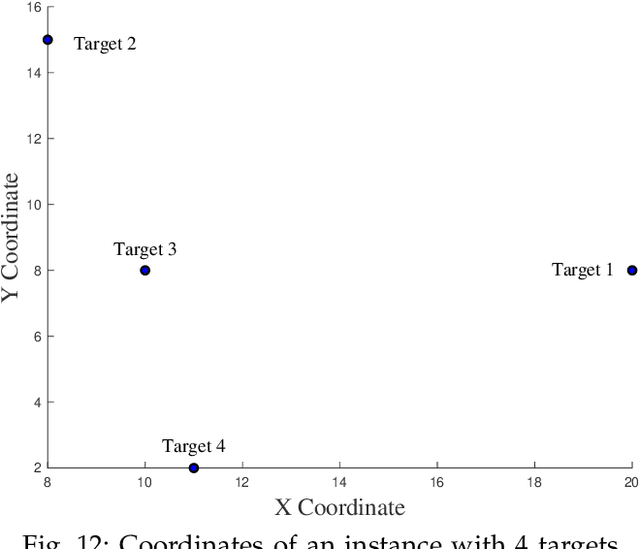
We consider the problem of planning a closed walk $\mathcal W$ for a UAV to persistently monitor a finite number of stationary targets with equal priorities and dynamically changing properties. A UAV must physically visit the targets in order to monitor them and collect information therein. The frequency of monitoring any given target is specified by a target revisit time, $i.e.$, the maximum allowable time between any two successive visits to the target. The problem considered in this paper is the following: Given $n$ targets and $k \geq n$ allowed visits to them, find an optimal closed walk $\mathcal W^*(k)$ so that every target is visited at least once and the maximum revisit time over all the targets, $\mathcal R(\mathcal W(k))$, is minimized. We prove the following: If $k \geq n^2-n$, $\mathcal R(\mathcal W^*(k))$ (or simply, $\mathcal R^*(k)$) takes only two values: $\mathcal R^*(n)$ when $k$ is an integral multiple of $n$, and $\mathcal R^*(n+1)$ otherwise. This result suggests significant computational savings - one only needs to determine $\mathcal W^*(n)$ and $\mathcal W^*(n+1)$ to construct an optimal solution $\mathcal W^*(k)$. We provide MILP formulations for computing $\mathcal W^*(n)$ and $\mathcal W^*(n+1)$. Furthermore, for {\it any} given $k$, we prove that $\mathcal R^*(k) \geq \mathcal R^*(k+n)$.