Equitable Routing -- Rethinking the Multiple Traveling Salesman Problem

The Multiple Traveling Salesman Problem (MTSP) with a single depot is a generalization of the well-known Traveling Salesman Problem (TSP) that involves an additional parameter, namely, the number of salesmen. In the MTSP, several salesmen at the depot need to visit a set of interconnected targets, such that each target is visited precisely once by at most one salesman while minimizing the total length of their tours. An equally important variant of the MTSP, the min-max MTSP, aims to distribute the workload (length of the individual tours) among salesmen by requiring the longest tour of all the salesmen to be as short as possible, i.e., minimizing the maximum tour length among all salesmen. The min-max MTSP appears in real-life applications to ensure a good balance of workloads for the salesmen. It is known in the literature that the min-max MTSP is notoriously difficult to solve to optimality due to the poor lower bounds its linear relaxations provide. In this paper, we formulate two novel parametric variants of the MTSP called the "fair-MTSP". One variant is formulated as a Mixed-Integer Second Order Cone Program (MISOCP), and the other as a Mixed Integer Linear Program (MILP). Both focus on enforcing the workloads for the salesmen to be equitable, i.e., the distribution of tour lengths for the salesmen to be fair while minimizing the total cost of their tours. We present algorithms to solve the two variants of the fair-MTSP to global optimality and computational results on benchmark and real-world test instances that make a case for fair-MTSP as a viable alternative to the min-max MTSP.

Assisted Path Planning for a UGV-UAV Team Through a Stochastic Network

In this article, we consider a multi-agent path planning problem in a stochastic environment. The environment, which can be an urban road network, is represented by a graph where the travel time for selected road segments (impeded edges) is a random variable because of traffic congestion. An unmanned ground vehicle (UGV) wishes to travel from a starting location to a destination while minimizing the arrival time at the destination. UGV can traverse through an impeded edge but the true travel time is only realized at the end of that edge. This implies that the UGV can potentially get stuck in an impeded edge with high travel time. A support vehicle, such as an unmanned aerial vehicle (UAV) is simultaneously deployed from its starting position to assist the UGV by inspecting and realizing the true cost of impeded edges. With the updated information from UAV, UGV can efficiently reroute its path to the destination. The UGV does not wait at any time until it reaches the destination. The UAV is permitted to terminate its path at any vertex. The goal is then to develop an online algorithm to determine efficient paths for the UGV and the UAV based on the current information so that the UGV reaches the destination in minimum time. We refer to this problem as Stochastic Assisted Path Planning (SAPP). We present Dynamic $k$-Shortest Path Planning (D*KSPP) algorithm for the UGV planning and Rural Postman Problem (RPP) formulation for the UAV planning. Due to the scalability challenges of RPP, we also present a heuristic based Priority Assignment Algorithm (PAA) for the UAV planning. Computational results are presented to corroborate the effectiveness of the proposed algorithm to solve SAPP.

Assisted Shortest Path Planning for a Convoy through a Repairable Network

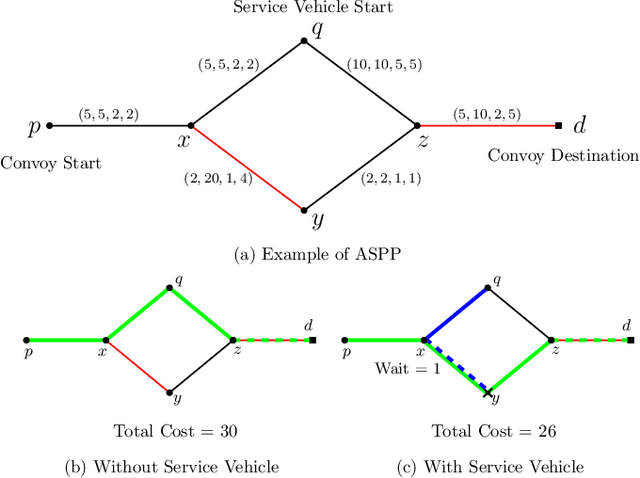
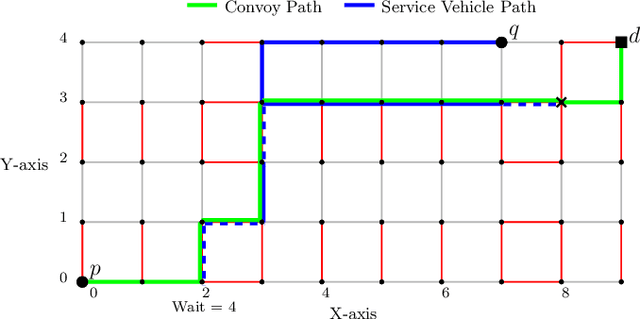
In this article, we consider a multi-agent path planning problem in a partially impeded environment. The impeded environment is represented by a graph with select road segments (edges) in disrepair impeding vehicular movement in the road network. A convoy wishes to travel from a starting location to a destination while minimizing some accumulated cost. The convoy may traverse an impeded edge for an additional cost (associated with repairing the edge) than if it were unimpeded. A second vehicle, referred to as a service vehicle, is simultaneously deployed with the convoy. The service vehicle assists the convoy by repairing an edge, reducing the cost for the convoy to traverse that edge. The convoy is permitted to wait at any vertex to allow the service vehicle to complete repairing an edge. The service vehicle is permitted to terminate its path at any vertex. The goal is then to find a pair of paths so the convoy reaches its destination while minimizing the total time (cost) the two vehicles are active, including any time the convoy waits. We refer to this problem as the Assisted Shortest Path Problem (ASPP). We present a generalized permanent labeling algorithm to find an optimal solution for the ASPP. We also introduce additional modifications to the labeling algorithm to significantly improve the computation time and refer to the modified labeling algorithm as $GPLA^*$. Computational results are presented to illustrate the effectiveness of $GPLA^*$ in solving the ASPP. We then give concluding remarks and briefly discuss potential variants of the ASPP for future work.