Multi Agent Pathfinding for Noise Restricted Hybrid Fuel Unmanned Aerial Vehicles

Multi Agent Path Finding (MAPF) seeks the optimal set of paths for multiple agents from respective start to goal locations such that no paths conflict. We address the MAPF problem for a fleet of hybrid-fuel unmanned aerial vehicles which are subject to location-dependent noise restrictions. We solve this problem by searching a constraint tree for which the subproblem at each node is a set of shortest path problems subject to the noise and fuel constraints and conflict zone avoidance. A labeling algorithm is presented to solve this subproblem, including the conflict zones which are treated as dynamic obstacles. We present the experimental results of the algorithms for various graph sizes and number of agents.

Assisted Path Planning for a UGV-UAV Team Through a Stochastic Network

In this article, we consider a multi-agent path planning problem in a stochastic environment. The environment, which can be an urban road network, is represented by a graph where the travel time for selected road segments (impeded edges) is a random variable because of traffic congestion. An unmanned ground vehicle (UGV) wishes to travel from a starting location to a destination while minimizing the arrival time at the destination. UGV can traverse through an impeded edge but the true travel time is only realized at the end of that edge. This implies that the UGV can potentially get stuck in an impeded edge with high travel time. A support vehicle, such as an unmanned aerial vehicle (UAV) is simultaneously deployed from its starting position to assist the UGV by inspecting and realizing the true cost of impeded edges. With the updated information from UAV, UGV can efficiently reroute its path to the destination. The UGV does not wait at any time until it reaches the destination. The UAV is permitted to terminate its path at any vertex. The goal is then to develop an online algorithm to determine efficient paths for the UGV and the UAV based on the current information so that the UGV reaches the destination in minimum time. We refer to this problem as Stochastic Assisted Path Planning (SAPP). We present Dynamic $k$-Shortest Path Planning (D*KSPP) algorithm for the UGV planning and Rural Postman Problem (RPP) formulation for the UAV planning. Due to the scalability challenges of RPP, we also present a heuristic based Priority Assignment Algorithm (PAA) for the UAV planning. Computational results are presented to corroborate the effectiveness of the proposed algorithm to solve SAPP.

Cooperative Coverage with a Leader and a Wingmate in Communication-Constrained Environments

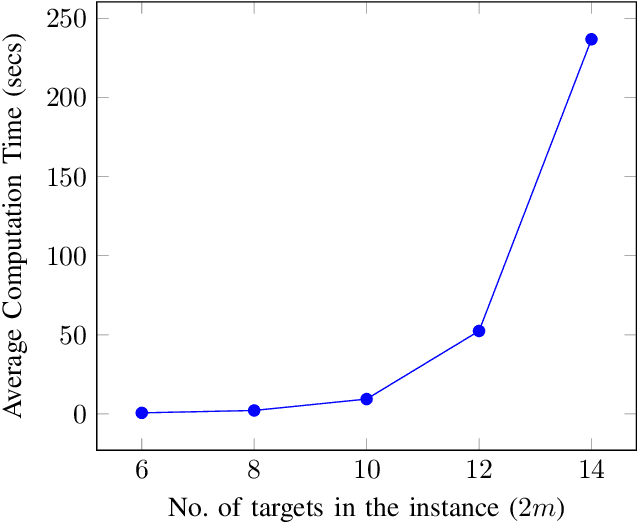
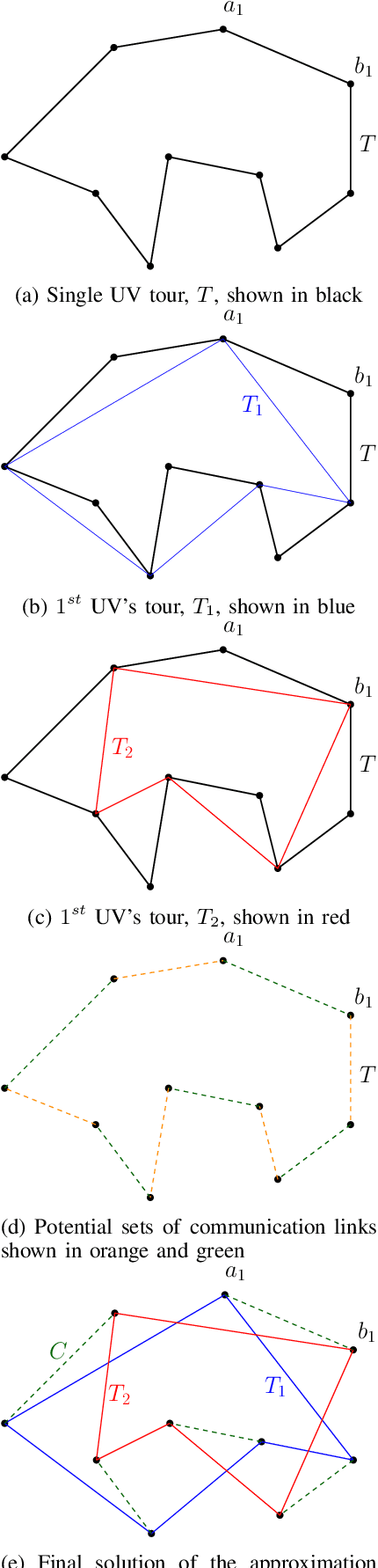
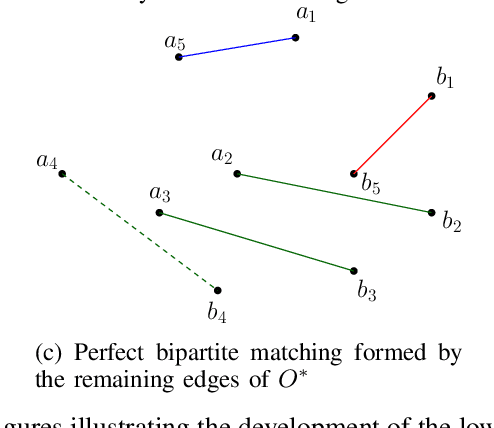
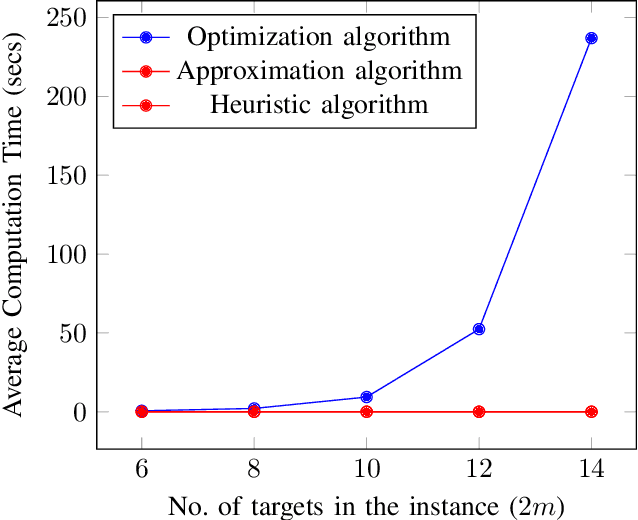
We consider a mission framework in which two unmanned vehicles (UVs), a leader and a wingmate, are required to provide cooperative coverage of an environment while being within a short communication range. This framework finds applications in underwater and/or military domains, where certain constraints are imposed on communication by either the application or the environment. An important objective of missions within this framework is to minimize the total travel and communication costs of the leader-wingmate duo. In this paper, we propose and formulate the problem of finding routes for the UVs that minimize the sum of their travel and communication costs as a network optimization problem of the form of a binary program (BP). The BP is computationally expensive, with the time required to compute optimal solutions increasing rapidly with the problem size. To address this challenge, here, we propose two algorithms, an approximation algorithm and a heuristic algorithm, to solve large-scale instances of the problem swiftly. We demonstrate the effectiveness and the scalability of these algorithms through an analysis of extensive numerical simulations performed over 500 instances, with the number of targets in the instances ranging from 6 to 100.

Assisted Shortest Path Planning for a Convoy through a Repairable Network

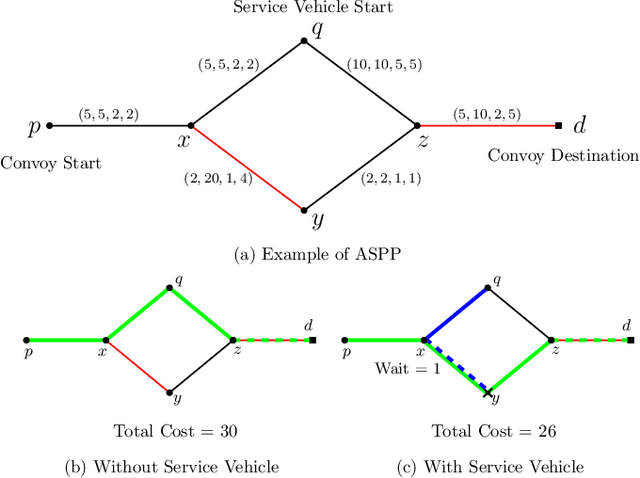
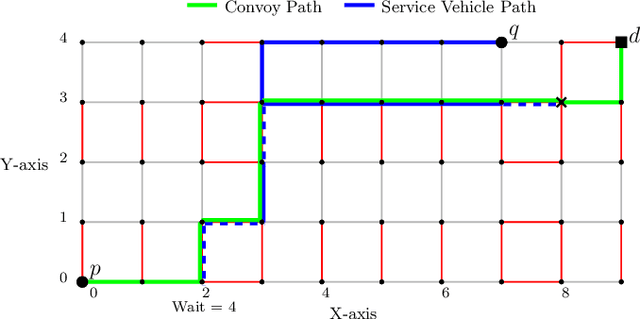
In this article, we consider a multi-agent path planning problem in a partially impeded environment. The impeded environment is represented by a graph with select road segments (edges) in disrepair impeding vehicular movement in the road network. A convoy wishes to travel from a starting location to a destination while minimizing some accumulated cost. The convoy may traverse an impeded edge for an additional cost (associated with repairing the edge) than if it were unimpeded. A second vehicle, referred to as a service vehicle, is simultaneously deployed with the convoy. The service vehicle assists the convoy by repairing an edge, reducing the cost for the convoy to traverse that edge. The convoy is permitted to wait at any vertex to allow the service vehicle to complete repairing an edge. The service vehicle is permitted to terminate its path at any vertex. The goal is then to find a pair of paths so the convoy reaches its destination while minimizing the total time (cost) the two vehicles are active, including any time the convoy waits. We refer to this problem as the Assisted Shortest Path Problem (ASPP). We present a generalized permanent labeling algorithm to find an optimal solution for the ASPP. We also introduce additional modifications to the labeling algorithm to significantly improve the computation time and refer to the modified labeling algorithm as $GPLA^*$. Computational results are presented to illustrate the effectiveness of $GPLA^*$ in solving the ASPP. We then give concluding remarks and briefly discuss potential variants of the ASPP for future work.