Differentially Private Stochastic Linear Bandits: (Almost) for Free

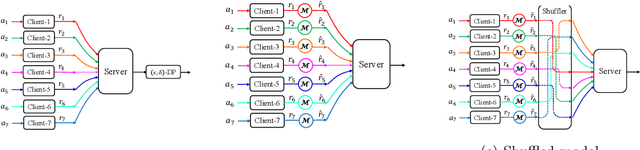
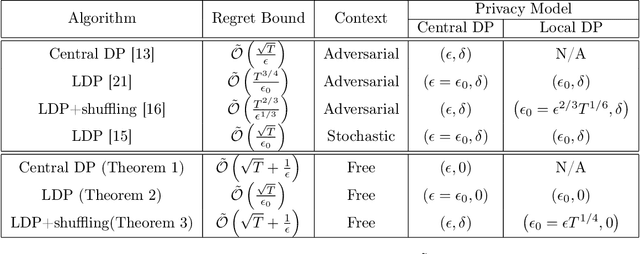
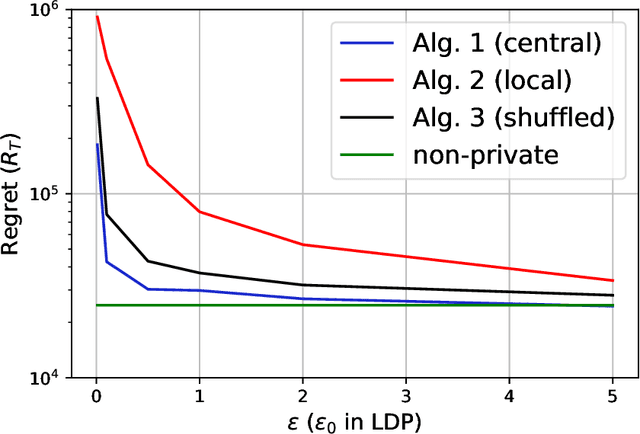
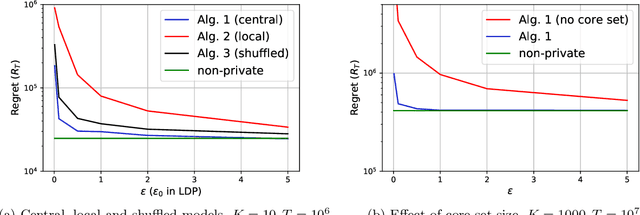
In this paper, we propose differentially private algorithms for the problem of stochastic linear bandits in the central, local and shuffled models. In the central model, we achieve almost the same regret as the optimal non-private algorithms, which means we get privacy for free. In particular, we achieve a regret of $\tilde{O}(\sqrt{T}+\frac{1}{\epsilon})$ matching the known lower bound for private linear bandits, while the best previously known algorithm achieves $\tilde{O}(\frac{1}{\epsilon}\sqrt{T})$. In the local case, we achieve a regret of $\tilde{O}(\frac{1}{\epsilon}{\sqrt{T}})$ which matches the non-private regret for constant $\epsilon$, but suffers a regret penalty when $\epsilon$ is small. In the shuffled model, we also achieve regret of $\tilde{O}(\sqrt{T}+\frac{1}{\epsilon})$ %for small $\epsilon$ as in the central case, while the best previously known algorithm suffers a regret of $\tilde{O}(\frac{1}{\epsilon}{T^{3/5}})$. Our numerical evaluation validates our theoretical results.

A Generative Framework for Personalized Learning and Estimation: Theory, Algorithms, and Privacy

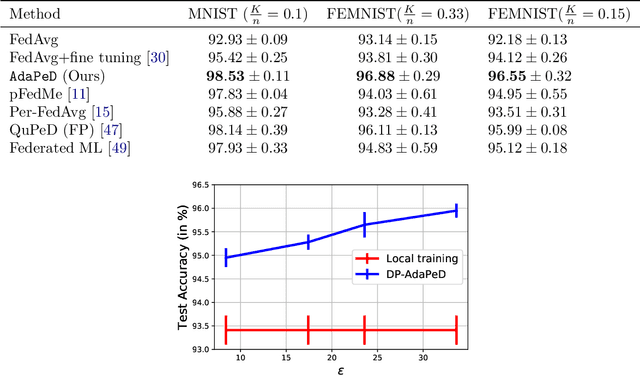
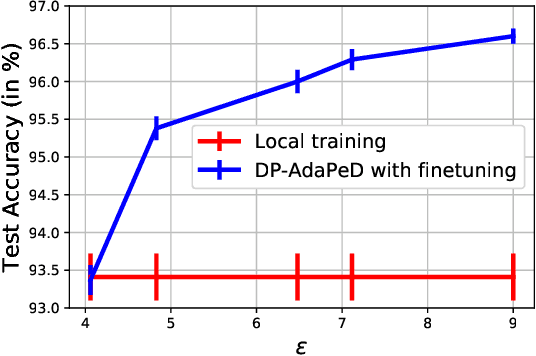
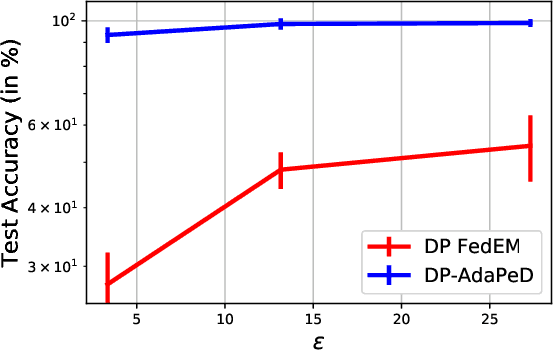
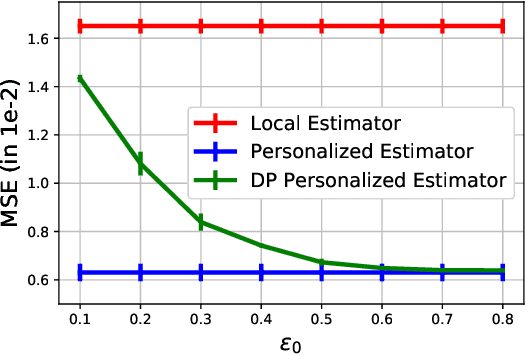
A distinguishing characteristic of federated learning is that the (local) client data could have statistical heterogeneity. This heterogeneity has motivated the design of personalized learning, where individual (personalized) models are trained, through collaboration. There have been various personalization methods proposed in literature, with seemingly very different forms and methods ranging from use of a single global model for local regularization and model interpolation, to use of multiple global models for personalized clustering, etc. In this work, we begin with a generative framework that could potentially unify several different algorithms as well as suggest new algorithms. We apply our generative framework to personalized estimation, and connect it to the classical empirical Bayes' methodology. We develop private personalized estimation under this framework. We then use our generative framework for learning, which unifies several known personalized FL algorithms and also suggests new ones; we propose and study a new algorithm AdaPeD based on a Knowledge Distillation, which numerically outperforms several known algorithms. We also develop privacy for personalized learning methods with guarantees for user-level privacy and composition. We numerically evaluate the performance as well as the privacy for both the estimation and learning problems, demonstrating the advantages of our proposed methods.

On Leave-One-Out Conditional Mutual Information For Generalization

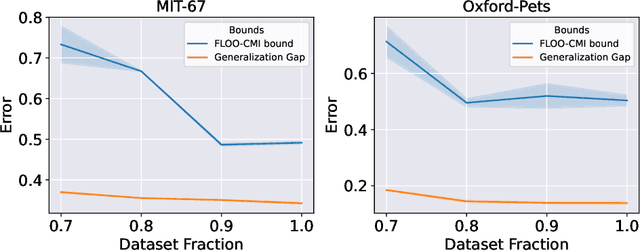
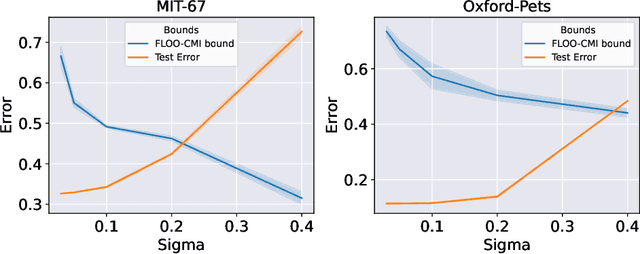
We derive information theoretic generalization bounds for supervised learning algorithms based on a new measure of leave-one-out conditional mutual information (loo-CMI). Contrary to other CMI bounds, which are black-box bounds that do not exploit the structure of the problem and may be hard to evaluate in practice, our loo-CMI bounds can be computed easily and can be interpreted in connection to other notions such as classical leave-one-out cross-validation, stability of the optimization algorithm, and the geometry of the loss-landscape. It applies both to the output of training algorithms as well as their predictions. We empirically validate the quality of the bound by evaluating its predicted generalization gap in scenarios for deep learning. In particular, our bounds are non-vacuous on large-scale image-classification tasks.

Decentralized Multi-Task Stochastic Optimization With Compressed Communications

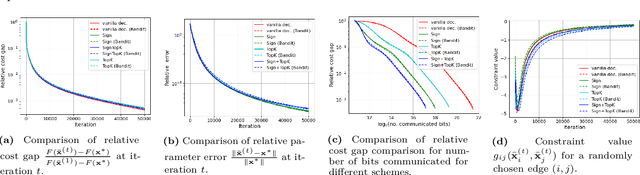
We consider a multi-agent network where each node has a stochastic (local) cost function that depends on the decision variable of that node and a random variable, and further the decision variables of neighboring nodes are pairwise constrained. There is an aggregate objective function for the network, composed additively of the expected values of the local cost functions at the nodes, and the overall goal of the network is to obtain the minimizing solution to this aggregate objective function subject to all the pairwise constraints. This is to be achieved at the node level using decentralized information and local computation, with exchanges of only compressed information allowed by neighboring nodes. The paper develops algorithms and obtains performance bounds for two different models of local information availability at the nodes: (i) sample feedback, where each node has direct access to samples of the local random variable to evaluate its local cost, and (ii) bandit feedback, where samples of the random variables are not available, but only the values of the local cost functions at two random points close to the decision are available to each node. For both models, with compressed communication between neighbors, we have developed decentralized saddle-point algorithms that deliver performances no different (in order sense) from those without communication compression; specifically, we show that deviation from the global minimum value and violations of the constraints are upper-bounded by $\mathcal{O}(T^{-\frac{1}{2}})$ and $\mathcal{O}(T^{-\frac{1}{4}})$, respectively, where $T$ is the number of iterations. Numerical examples provided in the paper corroborate these bounds and demonstrate the communication efficiency of the proposed method.

Coded Estimation: Design of Backscatter Array Codes for 3D Orientation Estimation

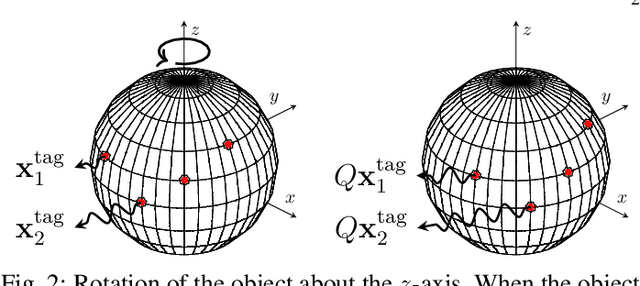
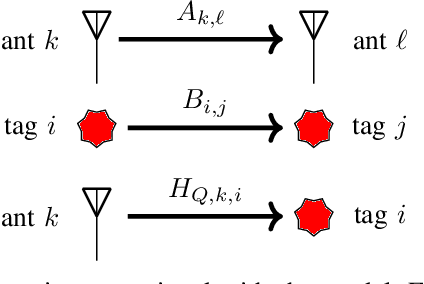
We consider the problem of estimating the orientation of a 3D object with the assistance of configurable backscatter tags. We explore the idea of designing tag response codes to improve the accuracy of orientation estimation. To minimize the difference between the true and estimated orientation, we propose two code design criteria. We also derive a lower bound on the worst-case error using Le Cam's method and provide simulation results for multiple scenarios including line-of-sight only and multipath, comparing the theoretical bounds to those achieved by the designs.

QuPeD: Quantized Personalization via Distillation with Applications to Federated Learning

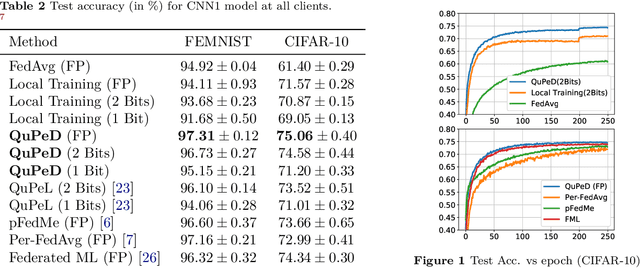
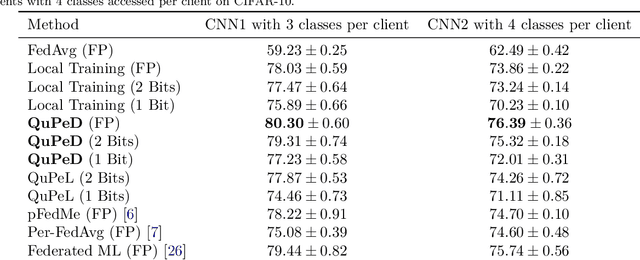
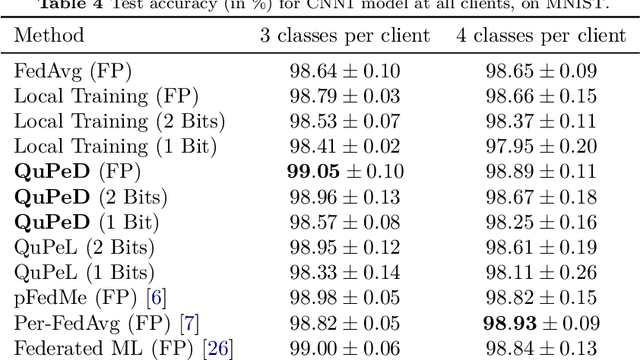
Traditionally, federated learning (FL) aims to train a single global model while collaboratively using multiple clients and a server. Two natural challenges that FL algorithms face are heterogeneity in data across clients and collaboration of clients with {\em diverse resources}. In this work, we introduce a \textit{quantized} and \textit{personalized} FL algorithm QuPeD that facilitates collective (personalized model compression) training via \textit{knowledge distillation} (KD) among clients who have access to heterogeneous data and resources. For personalization, we allow clients to learn \textit{compressed personalized models} with different quantization parameters and model dimensions/structures. Towards this, first we propose an algorithm for learning quantized models through a relaxed optimization problem, where quantization values are also optimized over. When each client participating in the (federated) learning process has different requirements for the compressed model (both in model dimension and precision), we formulate a compressed personalization framework by introducing knowledge distillation loss for local client objectives collaborating through a global model. We develop an alternating proximal gradient update for solving this compressed personalization problem, and analyze its convergence properties. Numerically, we validate that QuPeD outperforms competing personalized FL methods, FedAvg, and local training of clients in various heterogeneous settings.

Renyi Differential Privacy of the Subsampled Shuffle Model in Distributed Learning

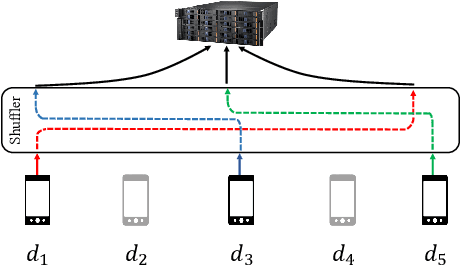
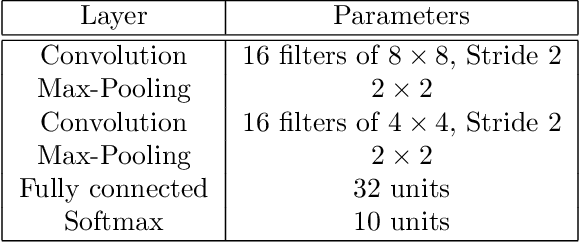
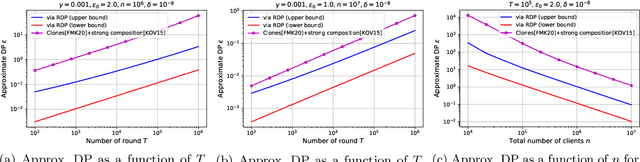
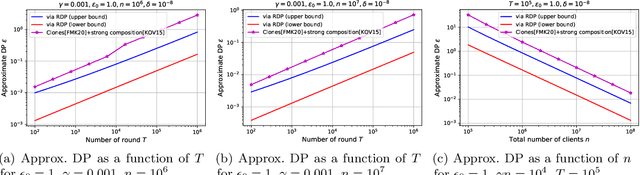
We study privacy in a distributed learning framework, where clients collaboratively build a learning model iteratively through interactions with a server from whom we need privacy. Motivated by stochastic optimization and the federated learning (FL) paradigm, we focus on the case where a small fraction of data samples are randomly sub-sampled in each round to participate in the learning process, which also enables privacy amplification. To obtain even stronger local privacy guarantees, we study this in the shuffle privacy model, where each client randomizes its response using a local differentially private (LDP) mechanism and the server only receives a random permutation (shuffle) of the clients' responses without their association to each client. The principal result of this paper is a privacy-optimization performance trade-off for discrete randomization mechanisms in this sub-sampled shuffle privacy model. This is enabled through a new theoretical technique to analyze the Renyi Differential Privacy (RDP) of the sub-sampled shuffle model. We numerically demonstrate that, for important regimes, with composition our bound yields significant improvement in privacy guarantee over the state-of-the-art approximate Differential Privacy (DP) guarantee (with strong composition) for sub-sampled shuffled models. We also demonstrate numerically significant improvement in privacy-learning performance operating point using real data sets.

A Field Guide to Federated Optimization

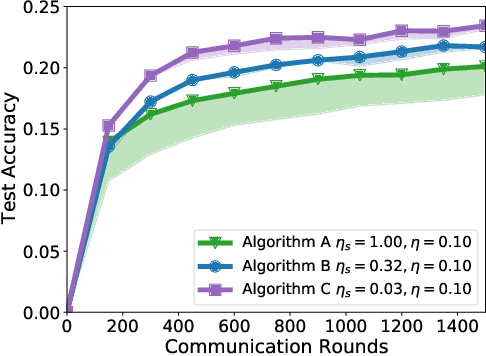
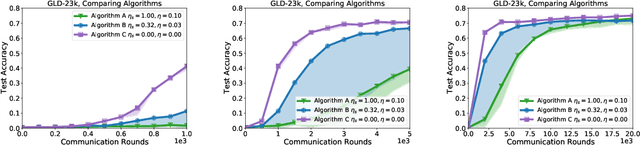
Federated learning and analytics are a distributed approach for collaboratively learning models (or statistics) from decentralized data, motivated by and designed for privacy protection. The distributed learning process can be formulated as solving federated optimization problems, which emphasize communication efficiency, data heterogeneity, compatibility with privacy and system requirements, and other constraints that are not primary considerations in other problem settings. This paper provides recommendations and guidelines on formulating, designing, evaluating and analyzing federated optimization algorithms through concrete examples and practical implementation, with a focus on conducting effective simulations to infer real-world performance. The goal of this work is not to survey the current literature, but to inspire researchers and practitioners to design federated learning algorithms that can be used in various practical applications.

On the Renyi Differential Privacy of the Shuffle Model

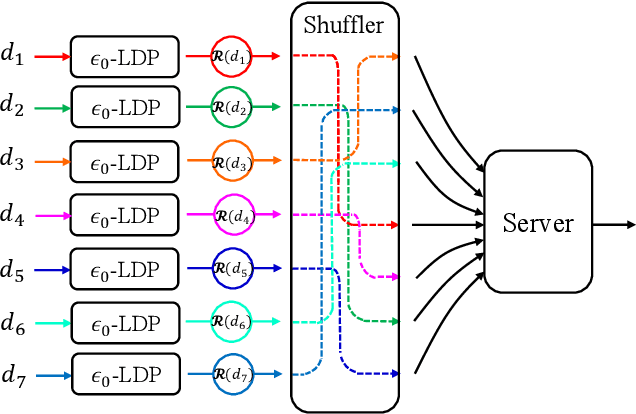
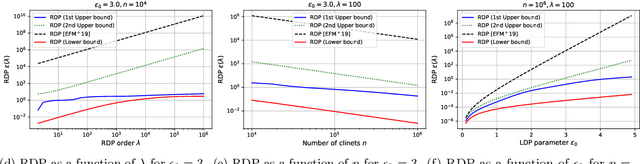
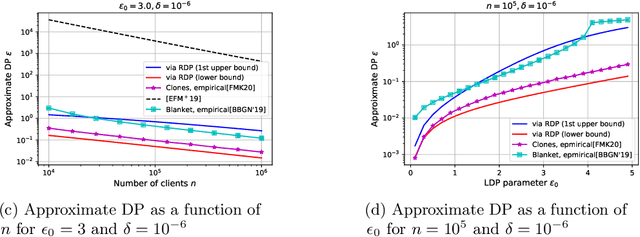
The central question studied in this paper is Renyi Differential Privacy (RDP) guarantees for general discrete local mechanisms in the shuffle privacy model. In the shuffle model, each of the $n$ clients randomizes its response using a local differentially private (LDP) mechanism and the untrusted server only receives a random permutation (shuffle) of the client responses without association to each client. The principal result in this paper is the first non-trivial RDP guarantee for general discrete local randomization mechanisms in the shuffled privacy model, and we develop new analysis techniques for deriving our results which could be of independent interest. In applications, such an RDP guarantee is most useful when we use it for composing several private interactions. We numerically demonstrate that, for important regimes, with composition our bound yields an improvement in privacy guarantee by a factor of $8\times$ over the state-of-the-art approximate Differential Privacy (DP) guarantee (with standard composition) for shuffled models. Moreover, combining with Poisson subsampling, our result leads to at least $10\times$ improvement over subsampled approximate DP with standard composition.

QuPeL: Quantized Personalization with Applications to Federated Learning

Traditionally, federated learning (FL) aims to train a single global model while collaboratively using multiple clients and a server. Two natural challenges that FL algorithms face are heterogeneity in data across clients and collaboration of clients with {\em diverse resources}. In this work, we introduce a \textit{quantized} and \textit{personalized} FL algorithm QuPeL that facilitates collective training with heterogeneous clients while respecting resource diversity. For personalization, we allow clients to learn \textit{compressed personalized models} with different quantization parameters depending on their resources. Towards this, first we propose an algorithm for learning quantized models through a relaxed optimization problem, where quantization values are also optimized over. When each client participating in the (federated) learning process has different requirements of the quantized model (both in value and precision), we formulate a quantized personalization framework by introducing a penalty term for local client objectives against a globally trained model to encourage collaboration. We develop an alternating proximal gradient update for solving this quantized personalization problem, and we analyze its convergence properties. Numerically, we show that optimizing over the quantization levels increases the performance and we validate that QuPeL outperforms both FedAvg and local training of clients in a heterogeneous setting.