Age-of-Gradient Updates for Federated Learning over Random Access Channels

This paper studies the problem of federated training of a deep neural network (DNN) over a random access channel (RACH) such as in computer networks, wireless networks, and cellular systems. More precisely, a set of remote users participate in training a centralized DNN model using SGD under the coordination of a parameter server (PS). The local model updates are transmitted from the remote users to the PS over a RACH using a slotted ALOHA protocol. The PS collects the updates from the remote users, accumulates them, and sends central model updates to the users at regular time intervals. We refer to this setting as the RACH-FL setting. The RACH-FL setting crucially addresses the problem of jointly designing a (i) client selection and (ii) gradient compression strategy which addresses the communication constraints between the remote users and the PS when transmission occurs over a RACH. For the RACH-FL setting, we propose a policy, which we term the ''age-of-gradient'' (AoG) policy in which (i) gradient sparsification is performed using top-K sparsification, (ii) the error correction is performed using memory accumulation, and (iii) the slot transmission probability is obtained by comparing the current local memory magnitude minus the magnitude of the gradient update to a threshold. Intuitively, the AoG measure of ''freshness'' of the memory state is reminiscent of the concept of age-of-information (AoI) in the context of communication theory and provides a rather natural interpretation of this policy. Numerical simulations show the superior performance of the AoG policy as compared to other RACH-FL policies.

HAAQI-Net: A non-intrusive neural music quality assessment model for hearing aids

This paper introduces HAAQI-Net, a non-intrusive deep learning model for music quality assessment tailored to hearing aid users. In contrast to traditional methods like the Hearing Aid Audio Quality Index (HAAQI), HAAQI-Net utilizes a Bidirectional Long Short-Term Memory (BLSTM) with attention. It takes an assessed music sample and a hearing loss pattern as input, generating a predicted HAAQI score. The model employs the pre-trained Bidirectional Encoder representation from Audio Transformers (BEATs) for acoustic feature extraction. Comparing predicted scores with ground truth, HAAQI-Net achieves a Longitudinal Concordance Correlation (LCC) of 0.9257, Spearman's Rank Correlation Coefficient (SRCC) of 0.9394, and Mean Squared Error (MSE) of 0.0080. Notably, this high performance comes with a substantial reduction in inference time: from 62.52 seconds (by HAAQI) to 2.71 seconds (by HAAQI-Net), serving as an efficient music quality assessment model for hearing aid users.

Harmonic Retrieval Using Weighted Lifted-Structure Low-Rank Matrix Completion

In this paper, we investigate the problem of recovering the frequency components of a mixture of $K$ complex sinusoids from a random subset of $N$ equally-spaced time-domain samples. Because of the random subset, the samples are effectively non-uniform. Besides, the frequency values of each of the $K$ complex sinusoids are assumed to vary continuously within a given range. For this problem, we propose a two-step strategy: (i) we first lift the incomplete set of uniform samples (unavailable samples are treated as missing data) into a structured matrix with missing entries, which is potentially low-rank; then (ii) we complete the matrix using a weighted nuclear minimization problem. We call the method a \emph{ weighted lifted-structured (WLi) low-rank matrix recovery}. Our approach can be applied to a range of matrix structures such as Hankel and double-Hankel, among others, and provides improvement over the unweighted existing schemes such as EMaC and DEMaC. We provide theoretical guarantees for the proposed method, as well as numerical simulations in both noiseless and noisy settings. Both the theoretical and the numerical results confirm the superiority of the proposed approach.

M22: A Communication-Efficient Algorithm for Federated Learning Inspired by Rate-Distortion

In federated learning (FL), the communication constraint between the remote learners and the Parameter Server (PS) is a crucial bottleneck. For this reason, model updates must be compressed so as to minimize the loss in accuracy resulting from the communication constraint. This paper proposes ``\emph{${\bf M}$-magnitude weighted $L_{\bf 2}$ distortion + $\bf 2$ degrees of freedom''} (M22) algorithm, a rate-distortion inspired approach to gradient compression for federated training of deep neural networks (DNNs). In particular, we propose a family of distortion measures between the original gradient and the reconstruction we referred to as ``$M$-magnitude weighted $L_2$'' distortion, and we assume that gradient updates follow an i.i.d. distribution -- generalized normal or Weibull, which have two degrees of freedom. In both the distortion measure and the gradient, there is one free parameter for each that can be fitted as a function of the iteration number. Given a choice of gradient distribution and distortion measure, we design the quantizer minimizing the expected distortion in gradient reconstruction. To measure the gradient compression performance under a communication constraint, we define the \emph{per-bit accuracy} as the optimal improvement in accuracy that one bit of communication brings to the centralized model over the training period. Using this performance measure, we systematically benchmark the choice of gradient distribution and distortion measure. We provide substantial insights on the role of these choices and argue that significant performance improvements can be attained using such a rate-distortion inspired compressor.

Empirical Risk Minimization with Generalized Relative Entropy Regularization

The empirical risk minimization (ERM) problem with relative entropy regularization (ERM-RER) is investigated under the assumption that the reference measure is a~$\sigma$-finite measure instead of a probability measure. This assumption leads to a generalization of the ERM-RER (g-ERM-RER) problem that allows for a larger degree of flexibility in the incorporation of prior knowledge over the set of models. The solution of the g-ERM-RER problem is shown to be a unique probability measure mutually absolutely continuous with the reference measure and to exhibit a probably-approximately-correct (PAC) guarantee for the ERM problem. For a given dataset, the empirical risk is shown to be a sub-Gaussian random variable when the models are sampled from the solution to the g-ERM-RER problem. Finally, the sensitivity of the expected empirical risk to deviations from the solution of the g-ERM-RER problem is studied. In particular, the expectation of the absolute value of sensitivity is shown to be upper bounded, up to a constant factor, by the square root of the lautum information between the models and the datasets.

Sharp asymptotics on the compression of two-layer neural networks

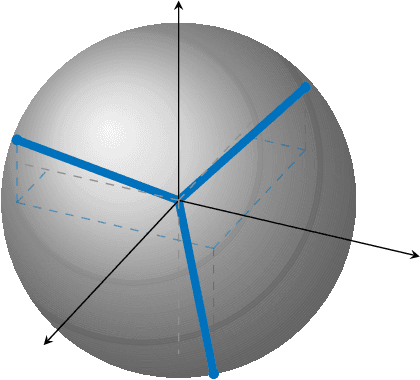
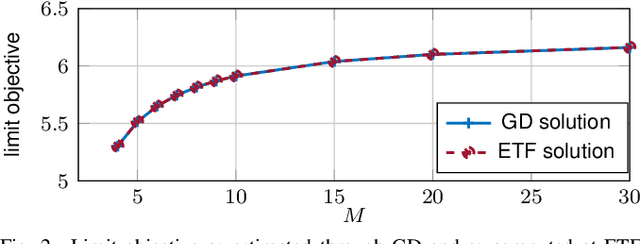
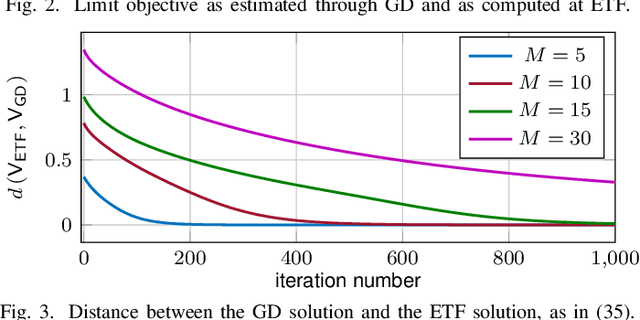
In this paper, we study the compression of a target two-layer neural network with N nodes into a compressed network with M < N nodes. More precisely, we consider the setting in which the weights of the target network are i.i.d. sub-Gaussian, and we minimize the population L2 loss between the outputs of the target and of the compressed network, under the assumption of Gaussian inputs. By using tools from high-dimensional probability, we show that this non-convex problem can be simplified when the target network is sufficiently over-parameterized, and provide the error rate of this approximation as a function of the input dimension and N . For a ReLU activation function, we conjecture that the optimum of the simplified optimization problem is achieved by taking weights on the Equiangular Tight Frame (ETF), while the scaling of the weights and the orientation of the ETF depend on the parameters of the target network. Numerical evidence is provided to support this conjecture.

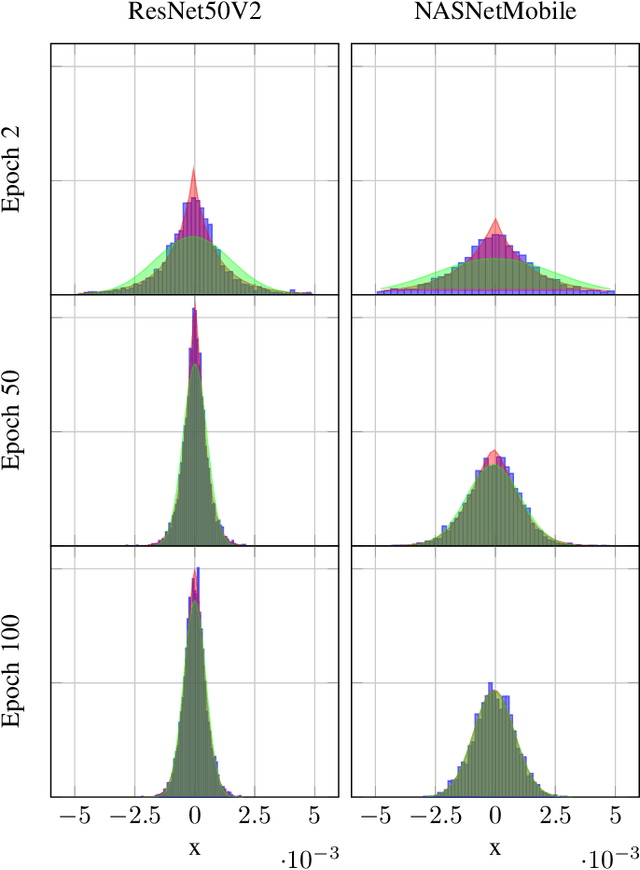
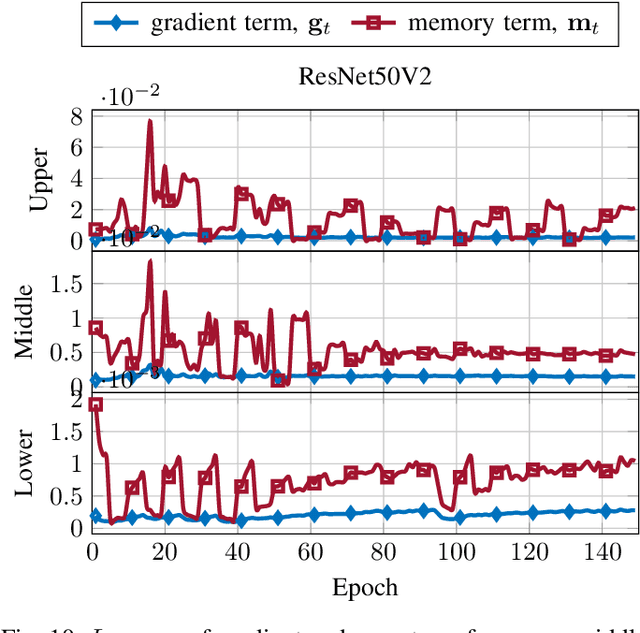
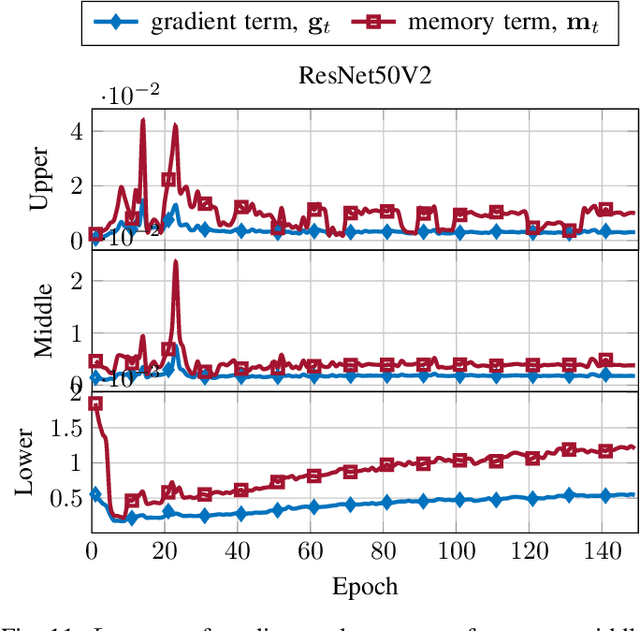
How to Attain Communication-Efficient DNN Training? Convert, Compress, Correct

In this paper, we introduce $\mathsf{CO}_3$, an algorithm for communication-efficiency federated Deep Neural Network (DNN) training.$\mathsf{CO}_3$ takes its name from three processing applied steps which reduce the communication load when transmitting the local gradients from the remote users to the Parameter Server.Namely:(i) gradient quantization through floating-point conversion, (ii) lossless compression of the quantized gradient, and (iii) quantization error correction.We carefully design each of the steps above so as to minimize the loss in the distributed DNN training when the communication overhead is fixed.In particular, in the design of steps (i) and (ii), we adopt the assumption that DNN gradients are distributed according to a generalized normal distribution.This assumption is validated numerically in the paper. For step (iii), we utilize an error feedback with memory decay mechanism to correct the quantization error introduced in step (i). We argue that this coefficient, similarly to the learning rate, can be optimally tuned to improve convergence. The performance of $\mathsf{CO}_3$ is validated through numerical simulations and is shown having better accuracy and improved stability at a reduced communication payload.

A Perspective on Neural Capacity Estimation: Viability and Reliability

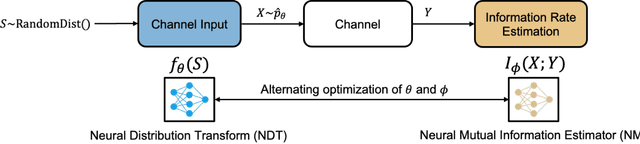
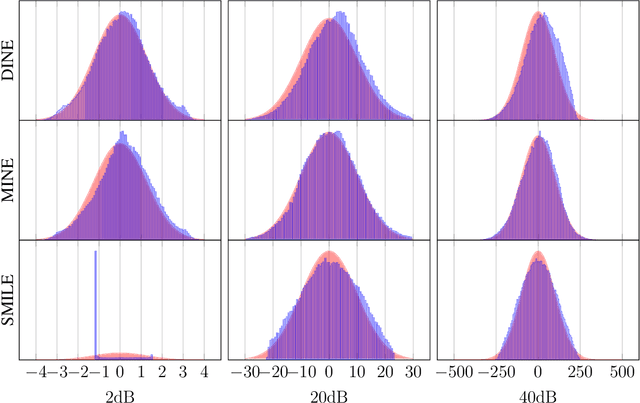
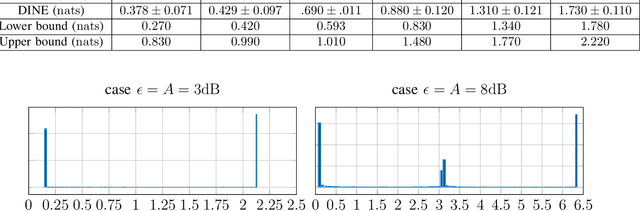
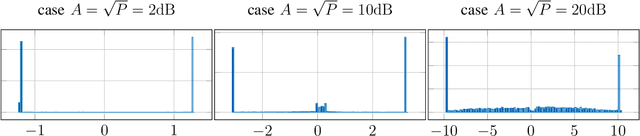
Recently, several methods have been proposed for estimating the mutual information from sample data using deep neural networks and without the knowledge of closed-form distribution of the data. This class of estimators is referred to as neural mutual information estimators (NMIE). In this paper, we investigate the performance of different NMIE proposed in the literature when applied to the capacity estimation problem. In particular, we study the performance of mutual information neural estimator (MINE), smoothed mutual information lower-bound estimator (SMILE), and directed information neural estimator (DINE). For the NMIE above, capacity estimation relies on two deep neural networks (DNN): (i) one DNN generates samples from a distribution that is learned, and (ii) a DNN to estimate the MI between the channel input and the channel output. We benchmark these NMIE in three scenarios: (i) AWGN channel capacity estimation and (ii) channels with unknown capacity and continuous inputs i.e., optical intensity and peak-power constrained AWGN channel (iii) channels with unknown capacity and a discrete number of mass points i.e., Poisson channel. Additionally, we also (iv) consider the extension to the MAC capacity problem by considering the AWGN and optical MAC models.

Convert, compress, correct: Three steps toward communication-efficient DNN training

In this paper, we introduce a novel algorithm, $\mathsf{CO}_3$, for communication-efficiency distributed Deep Neural Network (DNN) training. $\mathsf{CO}_3$ is a joint training/communication protocol, which encompasses three processing steps for the network gradients: (i) quantization through floating-point conversion, (ii) lossless compression, and (iii) error correction. These three components are crucial in the implementation of distributed DNN training over rate-constrained links. The interplay of these three steps in processing the DNN gradients is carefully balanced to yield a robust and high-performance scheme. The performance of the proposed scheme is investigated through numerical evaluations over CIFAR-10.

Two-snapshot DOA Estimation via Hankel-structured Matrix Completion

In this paper, we study the problem of estimating the direction of arrival (DOA) using a sparsely sampled uniform linear array (ULA). Based on an initial incomplete ULA measurement, our strategy is to choose a sparse subset of array elements for measuring the next snapshot. Then, we use a Hankel-structured matrix completion to interpolate for the missing ULA measurements. Finally, the source DOAs are estimated using a subspace method such as Prony on the fully recovered ULA. We theoretically provide a sufficient bound for the number of required samples (array elements) for perfect recovery. The numerical comparisons of the proposed method with existing techniques such as atomic-norm minimization and off-the-grid approaches confirm the superiority of the proposed method.