Mohammad Hossein Amani
Apertus: Democratizing Open and Compliant LLMs for Global Language Environments
Sep 17, 2025
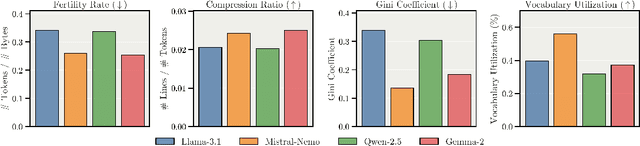

Abstract:We present Apertus, a fully open suite of large language models (LLMs) designed to address two systemic shortcomings in today's open model ecosystem: data compliance and multilingual representation. Unlike many prior models that release weights without reproducible data pipelines or regard for content-owner rights, Apertus models are pretrained exclusively on openly available data, retroactively respecting robots.txt exclusions and filtering for non-permissive, toxic, and personally identifiable content. To mitigate risks of memorization, we adopt the Goldfish objective during pretraining, strongly suppressing verbatim recall of data while retaining downstream task performance. The Apertus models also expand multilingual coverage, training on 15T tokens from over 1800 languages, with ~40% of pretraining data allocated to non-English content. Released at 8B and 70B scales, Apertus approaches state-of-the-art results among fully open models on multilingual benchmarks, rivalling or surpassing open-weight counterparts. Beyond model weights, we release all scientific artifacts from our development cycle with a permissive license, including data preparation scripts, checkpoints, evaluation suites, and training code, enabling transparent audit and extension.
Symbolic Autoencoding for Self-Supervised Sequence Learning
Feb 16, 2024Abstract:Traditional language models, adept at next-token prediction in text sequences, often struggle with transduction tasks between distinct symbolic systems, particularly when parallel data is scarce. Addressing this issue, we introduce \textit{symbolic autoencoding} ($\Sigma$AE), a self-supervised framework that harnesses the power of abundant unparallel data alongside limited parallel data. $\Sigma$AE connects two generative models via a discrete bottleneck layer and is optimized end-to-end by minimizing reconstruction loss (simultaneously with supervised loss for the parallel data), such that the sequence generated by the discrete bottleneck can be read out as the transduced input sequence. We also develop gradient-based methods allowing for efficient self-supervised sequence learning despite the discreteness of the bottleneck. Our results demonstrate that $\Sigma$AE significantly enhances performance on transduction tasks, even with minimal parallel data, offering a promising solution for weakly supervised learning scenarios.
Memorization and Optimization in Deep Neural Networks with Minimum Over-parameterization
May 20, 2022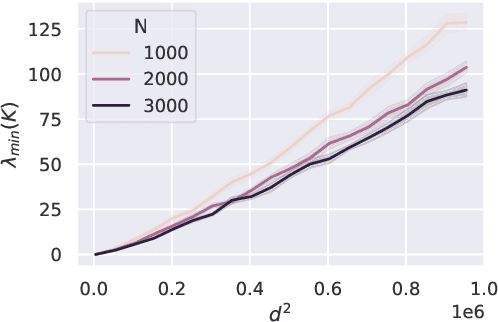
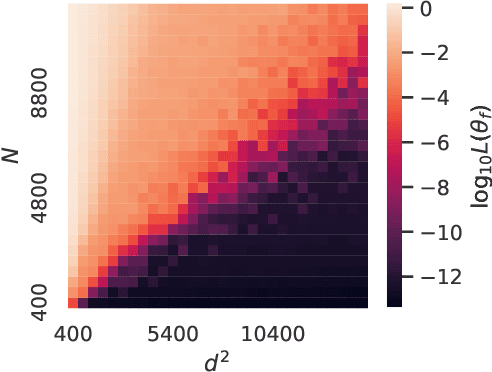
Abstract:The Neural Tangent Kernel (NTK) has emerged as a powerful tool to provide memorization, optimization and generalization guarantees in deep neural networks. A line of work has studied the NTK spectrum for two-layer and deep networks with at least a layer with $\Omega(N)$ neurons, $N$ being the number of training samples. Furthermore, there is increasing evidence suggesting that deep networks with sub-linear layer widths are powerful memorizers and optimizers, as long as the number of parameters exceeds the number of samples. Thus, a natural open question is whether the NTK is well conditioned in such a challenging sub-linear setup. In this paper, we answer this question in the affirmative. Our key technical contribution is a lower bound on the smallest NTK eigenvalue for deep networks with the minimum possible over-parameterization: the number of parameters is roughly $\Omega(N)$ and, hence, the number of neurons is as little as $\Omega(\sqrt{N})$. To showcase the applicability of our NTK bounds, we provide two results concerning memorization capacity and optimization guarantees for gradient descent training.
Sharp asymptotics on the compression of two-layer neural networks
May 18, 2022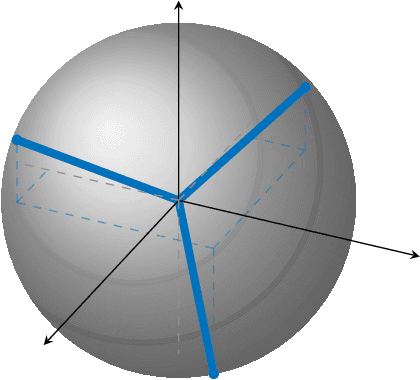
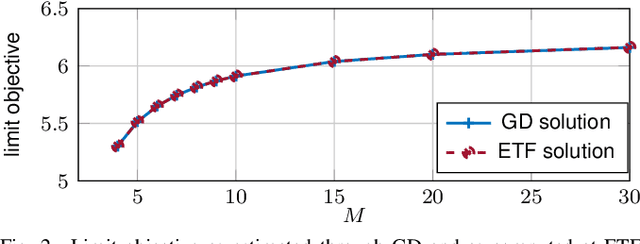
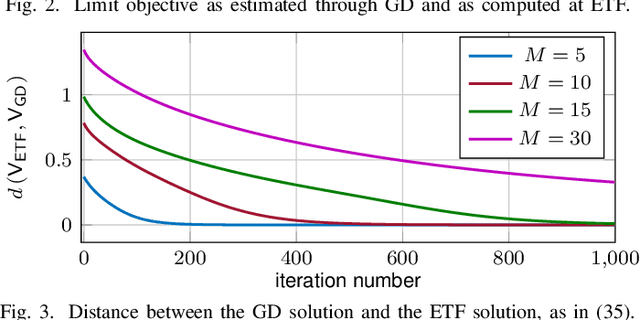

Abstract:In this paper, we study the compression of a target two-layer neural network with N nodes into a compressed network with M < N nodes. More precisely, we consider the setting in which the weights of the target network are i.i.d. sub-Gaussian, and we minimize the population L2 loss between the outputs of the target and of the compressed network, under the assumption of Gaussian inputs. By using tools from high-dimensional probability, we show that this non-convex problem can be simplified when the target network is sufficiently over-parameterized, and provide the error rate of this approximation as a function of the input dimension and N . For a ReLU activation function, we conjecture that the optimum of the simplified optimization problem is achieved by taking weights on the Equiangular Tight Frame (ETF), while the scaling of the weights and the orientation of the ETF depend on the parameters of the target network. Numerical evidence is provided to support this conjecture.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge