What data do we need for training an AV motion planner?

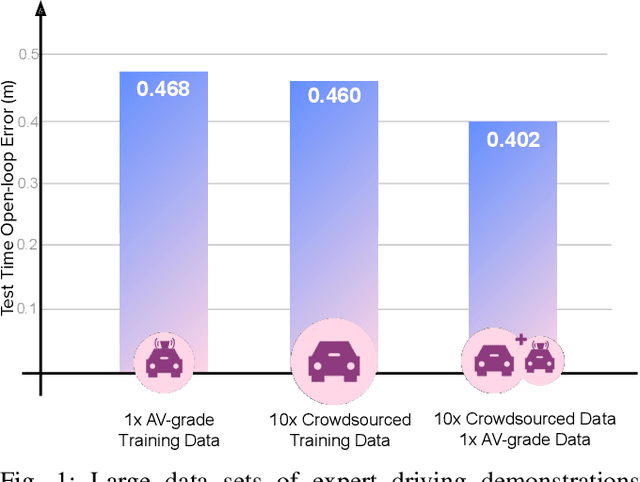
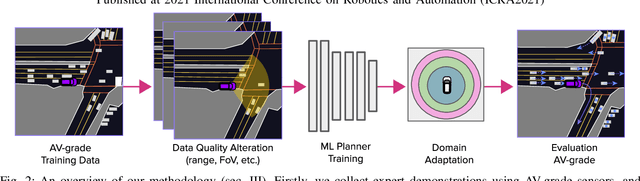
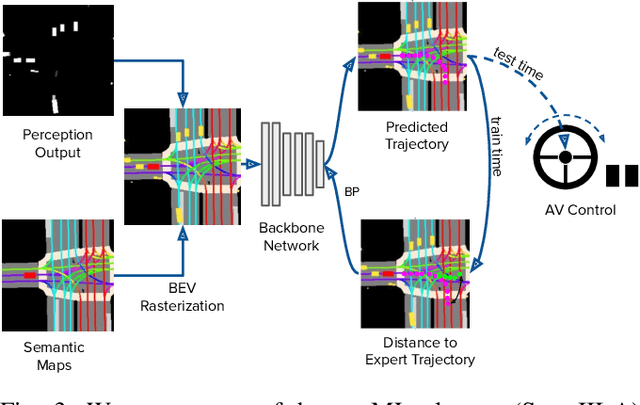
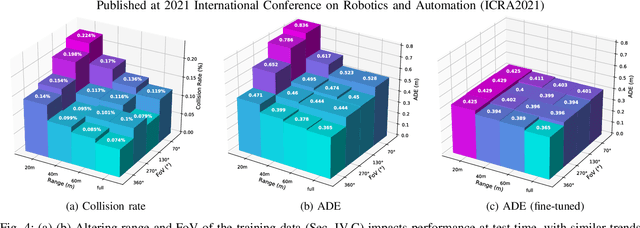
We investigate what grade of sensor data is required for training an imitation-learning-based AV planner on human expert demonstration. Machine-learned planners are very hungry for training data, which is usually collected using vehicles equipped with the same sensors used for autonomous operation. This is costly and non-scalable. If cheaper sensors could be used for collection instead, data availability would go up, which is crucial in a field where data volume requirements are large and availability is small. We present experiments using up to 1000 hours worth of expert demonstration and find that training with 10x lower-quality data outperforms 1x AV-grade data in terms of planner performance. The important implication of this is that cheaper sensors can indeed be used. This serves to improve data access and democratize the field of imitation-based motion planning. Alongside this, we perform a sensitivity analysis of planner performance as a function of perception range, field-of-view, accuracy, and data volume, and the reason why lower-quality data still provide good planning results.

Tractable Querying and Learning in Hybrid Domains via Sum-Product Networks

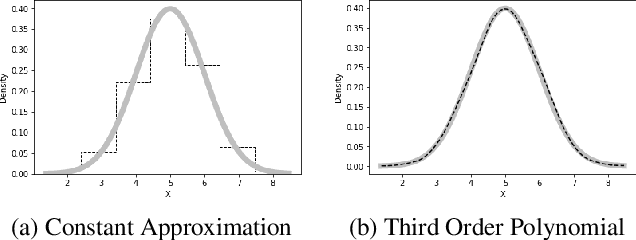
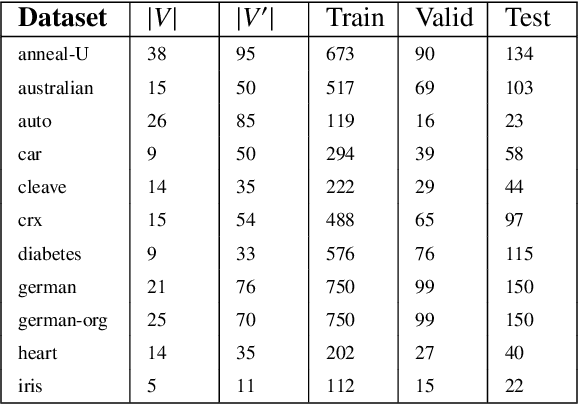
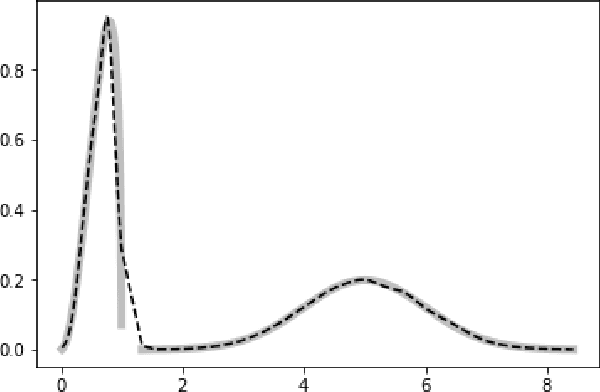
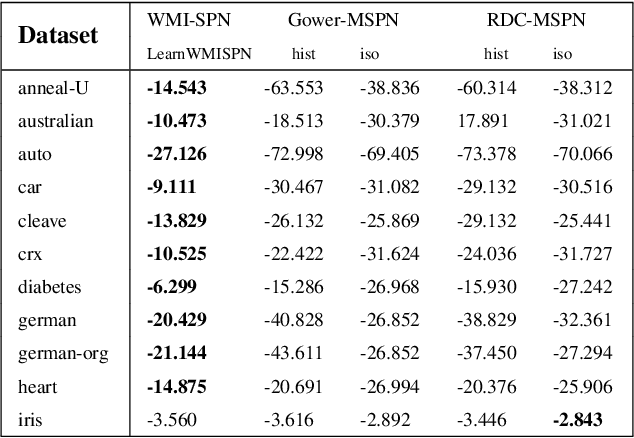
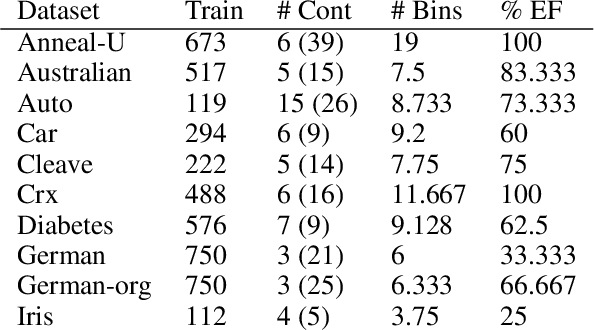
Probabilistic representations, such as Bayesian and Markov networks, are fundamental to much of statistical machine learning. Thus, learning probabilistic representations directly from data is a deep challenge, the main computational bottleneck being inference that is intractable. Tractable learning is a powerful new paradigm that attempts to learn distributions that support efficient probabilistic querying. By leveraging local structure, representations such as sum-product networks (SPNs) can capture high tree-width models with many hidden layers, essentially a deep architecture, while still admitting a range of probabilistic queries to be computable in time polynomial in the network size. The leaf nodes in SPNs, from which more intricate mixtures are formed, are tractable univariate distributions, and so the literature has focused on Bernoulli and Gaussian random variables. This is clearly a restriction for handling mixed discrete-continuous data, especially if the continuous features are generated from non-parametric and non-Gaussian distribution families. In this work, we present a framework that systematically integrates SPN structure learning with weighted model integration, a recently introduced computational abstraction for performing inference in hybrid domains, by means of piecewise polynomial approximations of density functions of arbitrary shape. Our framework is instantiated by exploiting the notion of propositional abstractions, thus minimally interfering with the SPN structure learning module, and supports a powerful query interface for conditioning on interval constraints. Our empirical results show that our approach is effective, and allows a study of the trade off between the granularity of the learned model and its predictive power.

Learning Probabilistic Logic Programs in Continuous Domains

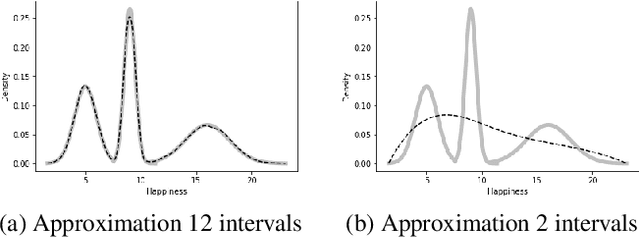
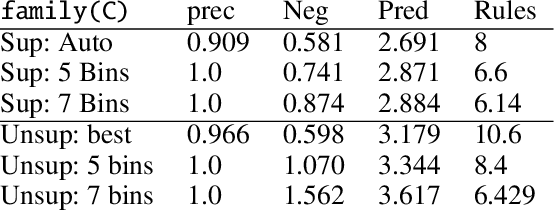
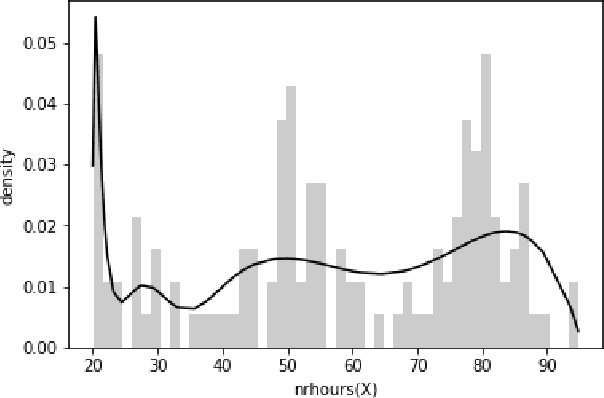
The field of statistical relational learning aims at unifying logic and probability to reason and learn from data. Perhaps the most successful paradigm in the field is probabilistic logic programming: the enabling of stochastic primitives in logic programming, which is now increasingly seen to provide a declarative background to complex machine learning applications. While many systems offer inference capabilities, the more significant challenge is that of learning meaningful and interpretable symbolic representations from data. In that regard, inductive logic programming and related techniques have paved much of the way for the last few decades. Unfortunately, a major limitation of this exciting landscape is that much of the work is limited to finite-domain discrete probability distributions. Recently, a handful of systems have been extended to represent and perform inference with continuous distributions. The problem, of course, is that classical solutions for inference are either restricted to well-known parametric families (e.g., Gaussians) or resort to sampling strategies that provide correct answers only in the limit. When it comes to learning, moreover, inducing representations remains entirely open, other than "data-fitting" solutions that force-fit points to aforementioned parametric families. In this paper, we take the first steps towards inducing probabilistic logic programs for continuous and mixed discrete-continuous data, without being pigeon-holed to a fixed set of distribution families. Our key insight is to leverage techniques from piecewise polynomial function approximation theory, yielding a principled way to learn and compositionally construct density functions. We test the framework and discuss the learned representations.