ODEFormer: Symbolic Regression of Dynamical Systems with Transformers

We introduce ODEFormer, the first transformer able to infer multidimensional ordinary differential equation (ODE) systems in symbolic form from the observation of a single solution trajectory. We perform extensive evaluations on two datasets: (i) the existing "Strogatz" dataset featuring two-dimensional systems; (ii) ODEBench, a collection of one- to four-dimensional systems that we carefully curated from the literature to provide a more holistic benchmark. ODEFormer consistently outperforms existing methods while displaying substantially improved robustness to noisy and irregularly sampled observations, as well as faster inference. We release our code, model and benchmark dataset publicly.

Boolformer: Symbolic Regression of Logic Functions with Transformers

In this work, we introduce Boolformer, the first Transformer architecture trained to perform end-to-end symbolic regression of Boolean functions. First, we show that it can predict compact formulas for complex functions which were not seen during training, when provided a clean truth table. Then, we demonstrate its ability to find approximate expressions when provided incomplete and noisy observations. We evaluate the Boolformer on a broad set of real-world binary classification datasets, demonstrating its potential as an interpretable alternative to classic machine learning methods. Finally, we apply it to the widespread task of modelling the dynamics of gene regulatory networks. Using a recent benchmark, we show that Boolformer is competitive with state-of-the art genetic algorithms with a speedup of several orders of magnitude. Our code and models are available publicly.

Length Generalization in Arithmetic Transformers

We examine how transformers cope with two challenges: learning basic integer arithmetic, and generalizing to longer sequences than seen during training. We find that relative position embeddings enable length generalization for simple tasks, such as addition: models trained on $5$-digit numbers can perform $15$-digit sums. However, this method fails for multiplication, and we propose train set priming: adding a few ($10$ to $50$) long sequences to the training set. We show that priming allows models trained on $5$-digit $\times$ $3$-digit multiplications to generalize to $35\times 3$ examples. We also show that models can be primed for different generalization lengths, and that the priming sample size scales as the logarithm of the training set size. Finally, we discuss potential applications of priming beyond arithmetic.

End-to-end symbolic regression with transformers

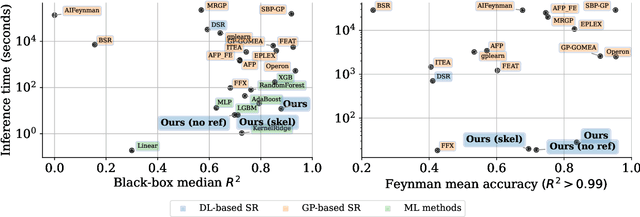
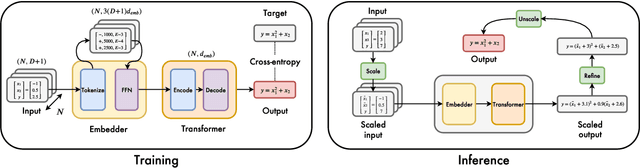
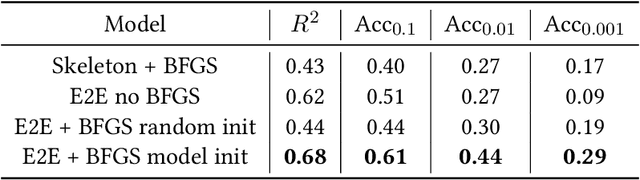
Symbolic regression, the task of predicting the mathematical expression of a function from the observation of its values, is a difficult task which usually involves a two-step procedure: predicting the "skeleton" of the expression up to the choice of numerical constants, then fitting the constants by optimizing a non-convex loss function. The dominant approach is genetic programming, which evolves candidates by iterating this subroutine a large number of times. Neural networks have recently been tasked to predict the correct skeleton in a single try, but remain much less powerful. In this paper, we challenge this two-step procedure, and task a Transformer to directly predict the full mathematical expression, constants included. One can subsequently refine the predicted constants by feeding them to the non-convex optimizer as an informed initialization. We present ablations to show that this end-to-end approach yields better results, sometimes even without the refinement step. We evaluate our model on problems from the SRBench benchmark and show that our model approaches the performance of state-of-the-art genetic programming with several orders of magnitude faster inference.

Optimal learning rate schedules in high-dimensional non-convex optimization problems

Learning rate schedules are ubiquitously used to speed up and improve optimisation. Many different policies have been introduced on an empirical basis, and theoretical analyses have been developed for convex settings. However, in many realistic problems the loss-landscape is high-dimensional and non convex -- a case for which results are scarce. In this paper we present a first analytical study of the role of learning rate scheduling in this setting, focusing on Langevin optimization with a learning rate decaying as $\eta(t)=t^{-\beta}$. We begin by considering models where the loss is a Gaussian random function on the $N$-dimensional sphere ($N\rightarrow \infty$), featuring an extensive number of critical points. We find that to speed up optimization without getting stuck in saddles, one must choose a decay rate $\beta<1$, contrary to convex setups where $\beta=1$ is generally optimal. We then add to the problem a signal to be recovered. In this setting, the dynamics decompose into two phases: an \emph{exploration} phase where the dynamics navigates through rough parts of the landscape, followed by a \emph{convergence} phase where the signal is detected and the dynamics enter a convex basin. In this case, it is optimal to keep a large learning rate during the exploration phase to escape the non-convex region as quickly as possible, then use the convex criterion $\beta=1$ to converge rapidly to the solution. Finally, we demonstrate that our conclusions hold in a common regression task involving neural networks.

Deep Symbolic Regression for Recurrent Sequences

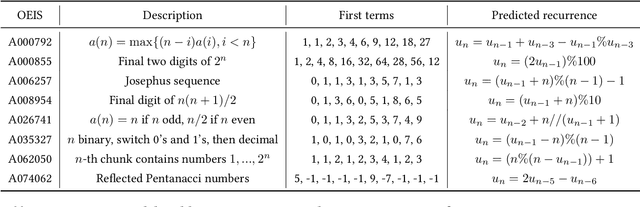
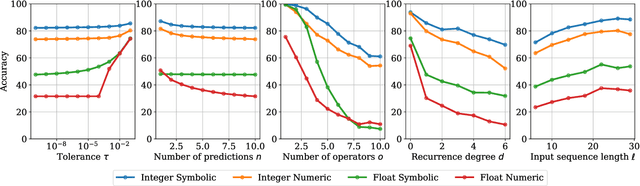
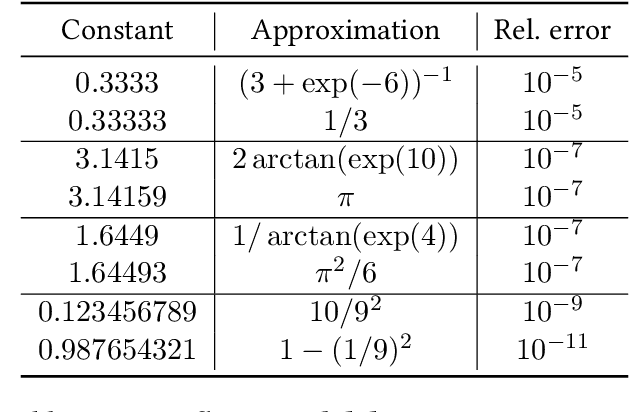
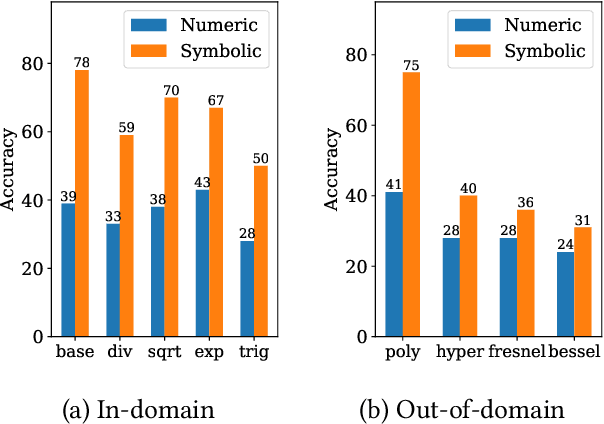
Symbolic regression, i.e. predicting a function from the observation of its values, is well-known to be a challenging task. In this paper, we train Transformers to infer the function or recurrence relation underlying sequences of integers or floats, a typical task in human IQ tests which has hardly been tackled in the machine learning literature. We evaluate our integer model on a subset of OEIS sequences, and show that it outperforms built-in Mathematica functions for recurrence prediction. We also demonstrate that our float model is able to yield informative approximations of out-of-vocabulary functions and constants, e.g. $\operatorname{bessel0}(x)\approx \frac{\sin(x)+\cos(x)}{\sqrt{\pi x}}$ and $1.644934\approx \pi^2/6$. An interactive demonstration of our models is provided at https://bit.ly/3niE5FS.

Transformed CNNs: recasting pre-trained convolutional layers with self-attention

Vision Transformers (ViT) have recently emerged as a powerful alternative to convolutional networks (CNNs). Although hybrid models attempt to bridge the gap between these two architectures, the self-attention layers they rely on induce a strong computational bottleneck, especially at large spatial resolutions. In this work, we explore the idea of reducing the time spent training these layers by initializing them as convolutional layers. This enables us to transition smoothly from any pre-trained CNN to its functionally identical hybrid model, called Transformed CNN (T-CNN). With only 50 epochs of fine-tuning, the resulting T-CNNs demonstrate significant performance gains over the CNN (+2.2% top-1 on ImageNet-1k for a ResNet50-RS) as well as substantially improved robustness (+11% top-1 on ImageNet-C). We analyze the representations learnt by the T-CNN, providing deeper insights into the fruitful interplay between convolutions and self-attention. Finally, we experiment initializing the T-CNN from a partially trained CNN, and find that it reaches better performance than the corresponding hybrid model trained from scratch, while reducing training time.

ConViT: Improving Vision Transformers with Soft Convolutional Inductive Biases

Convolutional architectures have proven extremely successful for vision tasks. Their hard inductive biases enable sample-efficient learning, but come at the cost of a potentially lower performance ceiling. Vision Transformers (ViTs) rely on more flexible self-attention layers, and have recently outperformed CNNs for image classification. However, they require costly pre-training on large external datasets or distillation from pre-trained convolutional networks. In this paper, we ask the following question: is it possible to combine the strengths of these two architectures while avoiding their respective limitations? To this end, we introduce gated positional self-attention (GPSA), a form of positional self-attention which can be equipped with a "soft" convolutional inductive bias. We initialize the GPSA layers to mimic the locality of convolutional layers, then give each attention head the freedom to escape locality by adjusting a gating parameter regulating the attention paid to position versus content information. The resulting convolutional-like ViT architecture, ConViT, outperforms the DeiT on ImageNet, while offering a much improved sample efficiency. We further investigate the role of locality in learning by first quantifying how it is encouraged in vanilla self-attention layers, then analyzing how it is escaped in GPSA layers. We conclude by presenting various ablations to better understand the success of the ConViT. Our code and models are released publicly.

More data or more parameters? Investigating the effect of data structure on generalization

One of the central features of deep learning is the generalization abilities of neural networks, which seem to improve relentlessly with over-parametrization. In this work, we investigate how properties of data impact the test error as a function of the number of training examples and number of training parameters; in other words, how the structure of data shapes the "generalization phase space". We first focus on the random features model trained in the teacher-student scenario. The synthetic input data is composed of independent blocks, which allow us to tune the saliency of low-dimensional structures and their relevance with respect to the target function. Using methods from statistical physics, we obtain an analytical expression for the train and test errors for both regression and classification tasks in the high-dimensional limit. The derivation allows us to show that noise in the labels and strong anisotropy of the input data play similar roles on the test error. Both promote an asymmetry of the phase space where increasing the number of training examples improves generalization further than increasing the number of training parameters. Our analytical insights are confirmed by numerical experiments involving fully-connected networks trained on MNIST and CIFAR10.

The dynamics of learning with feedback alignment

Direct Feedback Alignment (DFA) is emerging as an efficient and biologically plausible alternative to the ubiquitous backpropagation algorithm for training deep neural networks. Despite relying on random feedback weights for the backward pass, DFA successfully trains state-of-the-art models such as Transformers. On the other hand, it notoriously fails to train convolutional networks. An understanding of the inner workings of DFA to explain these diverging results remains elusive. Here, we propose a theory for the success of DFA. We first show that learning in shallow networks proceeds in two steps: an alignment phase, where the model adapts its weights to align the approximate gradient with the true gradient of the loss function, is followed by a memorisation phase, where the model focuses on fitting the data. This two-step process has a degeneracy breaking effect: out of all the low-loss solutions in the landscape, a network trained with DFA naturally converges to the solution which maximises gradient alignment. We also identify a key quantity underlying alignment in deep linear networks: the conditioning of the alignment matrices. The latter enables a detailed understanding of the impact of data structure on alignment, and suggests a simple explanation for the well-known failure of DFA to train convolutional neural networks. Numerical experiments on MNIST and CIFAR10 clearly demonstrate degeneracy breaking in deep non-linear networks and show that the align-then-memorize process occurs sequentially from the bottom layers of the network to the top.