Identifiability Challenges in Sparse Linear Ordinary Differential Equations

Dynamical systems modeling is a core pillar of scientific inquiry across natural and life sciences. Increasingly, dynamical system models are learned from data, rendering identifiability a paramount concept. For systems that are not identifiable from data, no guarantees can be given about their behavior under new conditions and inputs, or about possible control mechanisms to steer the system. It is known in the community that "linear ordinary differential equations (ODE) are almost surely identifiable from a single trajectory." However, this only holds for dense matrices. The sparse regime remains underexplored, despite its practical relevance with sparsity arising naturally in many biological, social, and physical systems. In this work, we address this gap by characterizing the identifiability of sparse linear ODEs. Contrary to the dense case, we show that sparse systems are unidentifiable with a positive probability in practically relevant sparsity regimes and provide lower bounds for this probability. We further study empirically how this theoretical unidentifiability manifests in state-of-the-art methods to estimate linear ODEs from data. Our results corroborate that sparse systems are also practically unidentifiable. Theoretical limitations are not resolved through inductive biases or optimization dynamics. Our findings call for rethinking what can be expected from data-driven dynamical system modeling and allows for quantitative assessments of how much to trust a learned linear ODE.

ODEFormer: Symbolic Regression of Dynamical Systems with Transformers

We introduce ODEFormer, the first transformer able to infer multidimensional ordinary differential equation (ODE) systems in symbolic form from the observation of a single solution trajectory. We perform extensive evaluations on two datasets: (i) the existing "Strogatz" dataset featuring two-dimensional systems; (ii) ODEBench, a collection of one- to four-dimensional systems that we carefully curated from the literature to provide a more holistic benchmark. ODEFormer consistently outperforms existing methods while displaying substantially improved robustness to noisy and irregularly sampled observations, as well as faster inference. We release our code, model and benchmark dataset publicly.

Predicting Ordinary Differential Equations with Transformers

We develop a transformer-based sequence-to-sequence model that recovers scalar ordinary differential equations (ODEs) in symbolic form from irregularly sampled and noisy observations of a single solution trajectory. We demonstrate in extensive empirical evaluations that our model performs better or on par with existing methods in terms of accurate recovery across various settings. Moreover, our method is efficiently scalable: after one-time pretraining on a large set of ODEs, we can infer the governing law of a new observed solution in a few forward passes of the model.

Discovering ordinary differential equations that govern time-series

Natural laws are often described through differential equations yet finding a differential equation that describes the governing law underlying observed data is a challenging and still mostly manual task. In this paper we make a step towards the automation of this process: we propose a transformer-based sequence-to-sequence model that recovers scalar autonomous ordinary differential equations (ODEs) in symbolic form from time-series data of a single observed solution of the ODE. Our method is efficiently scalable: after one-time pretraining on a large set of ODEs, we can infer the governing laws of a new observed solution in a few forward passes of the model. Then we show that our model performs better or on par with existing methods in various test cases in terms of accurate symbolic recovery of the ODE, especially for more complex expressions.

Curiously Effective Features for Image Quality Prediction

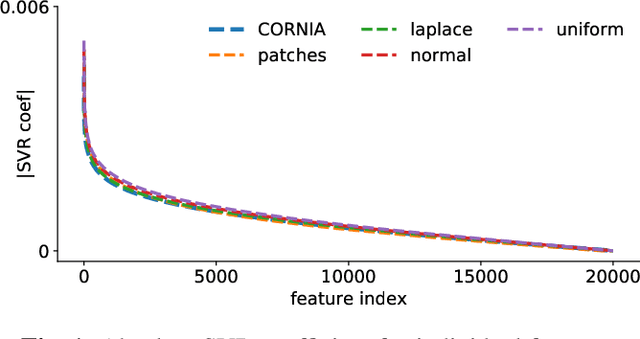
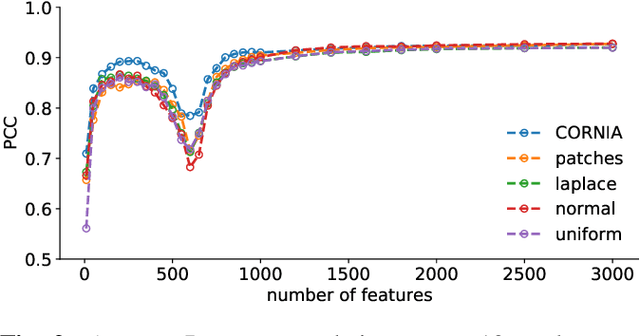
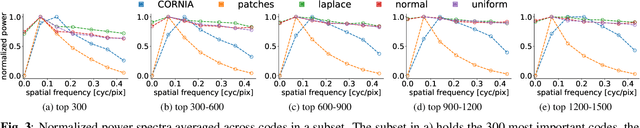
The performance of visual quality prediction models is commonly assumed to be closely tied to their ability to capture perceptually relevant image aspects. Models are thus either based on sophisticated feature extractors carefully designed from extensive domain knowledge or optimized through feature learning. In contrast to this, we find feature extractors constructed from random noise to be sufficient to learn a linear regression model whose quality predictions reach high correlations with human visual quality ratings, on par with a model with learned features. We analyze this curious result and show that besides the quality of feature extractors also their quantity plays a crucial role - with top performances only being achieved in highly overparameterized models.

Interpreting and Explaining Deep Neural Networks for Classification of Audio Signals

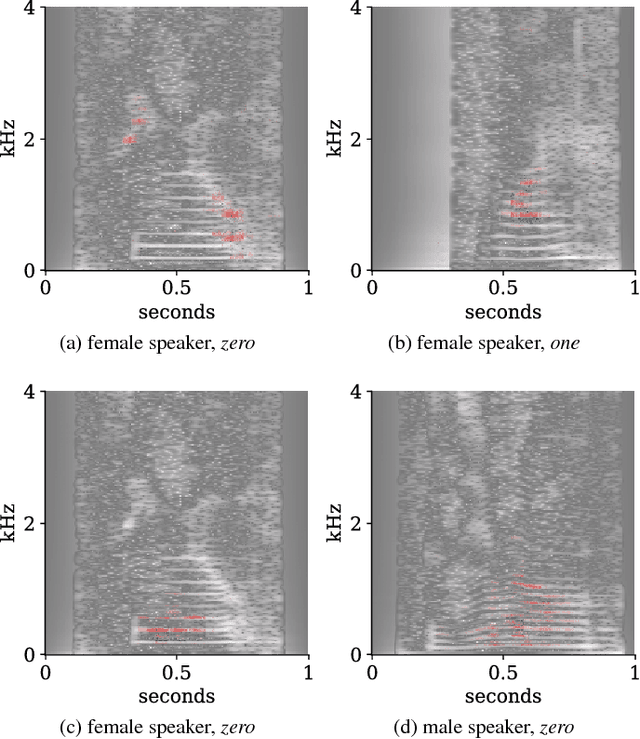
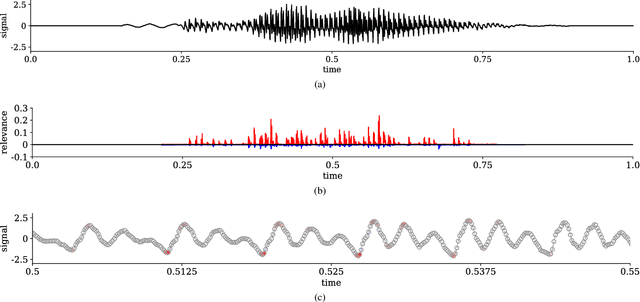
Interpretability of deep neural networks is a recently emerging area of machine learning research targeting a better understanding of how models perform feature selection and derive their classification decisions. In this paper, two neural network architectures are trained on spectrogram and raw waveform data for audio classification tasks on a newly created audio dataset and layer-wise relevance propagation (LRP), a previously proposed interpretability method, is applied to investigate the models' feature selection and decision making. It is demonstrated that the networks are highly reliant on feature marked as relevant by LRP through systematic manipulation of the input data. Our results show that by making deep audio classifiers interpretable, one can analyze and compare the properties and strategies of different models beyond classification accuracy, which potentially opens up new ways for model improvements.