Revisiting the Robustness of the Minimum Error Entropy Criterion: A Transfer Learning Case Study

Coping with distributional shifts is an important part of transfer learning methods in order to perform well in real-life tasks. However, most of the existing approaches in this area either focus on an ideal scenario in which the data does not contain noises or employ a complicated training paradigm or model design to deal with distributional shifts. In this paper, we revisit the robustness of the minimum error entropy (MEE) criterion, a widely used objective in statistical signal processing to deal with non-Gaussian noises, and investigate its feasibility and usefulness in real-life transfer learning regression tasks, where distributional shifts are common. Specifically, we put forward a new theoretical result showing the robustness of MEE against covariate shift. We also show that by simply replacing the mean squared error (MSE) loss with the MEE on basic transfer learning algorithms such as fine-tuning and linear probing, we can achieve competitive performance with respect to state-of-the-art transfer learning algorithms. We justify our arguments on both synthetic data and 5 real-world time-series data.

Coping with Change: Learning Invariant and Minimum Sufficient Representations for Fine-Grained Visual Categorization

Fine-grained visual categorization (FGVC) is a challenging task due to similar visual appearances between various species. Previous studies always implicitly assume that the training and test data have the same underlying distributions, and that features extracted by modern backbone architectures remain discriminative and generalize well to unseen test data. However, we empirically justify that these conditions are not always true on benchmark datasets. To this end, we combine the merits of invariant risk minimization (IRM) and information bottleneck (IB) principle to learn invariant and minimum sufficient (IMS) representations for FGVC, such that the overall model can always discover the most succinct and consistent fine-grained features. We apply the matrix-based R{\'e}nyi's $\alpha$-order entropy to simplify and stabilize the training of IB; we also design a ``soft" environment partition scheme to make IRM applicable to FGVC task. To the best of our knowledge, we are the first to address the problem of FGVC from a generalization perspective and develop a new information-theoretic solution accordingly. Extensive experiments demonstrate the consistent performance gain offered by our IMS.

The Conditional Cauchy-Schwarz Divergence with Applications to Time-Series Data and Sequential Decision Making

The Cauchy-Schwarz (CS) divergence was developed by Pr\'{i}ncipe et al. in 2000. In this paper, we extend the classic CS divergence to quantify the closeness between two conditional distributions and show that the developed conditional CS divergence can be simply estimated by a kernel density estimator from given samples. We illustrate the advantages (e.g., the rigorous faithfulness guarantee, the lower computational complexity, the higher statistical power, and the much more flexibility in a wide range of applications) of our conditional CS divergence over previous proposals, such as the conditional KL divergence and the conditional maximum mean discrepancy. We also demonstrate the compelling performance of conditional CS divergence in two machine learning tasks related to time series data and sequential inference, namely the time series clustering and the uncertainty-guided exploration for sequential decision making.

Causal Recurrent Variational Autoencoder for Medical Time Series Generation

We propose causal recurrent variational autoencoder (CR-VAE), a novel generative model that is able to learn a Granger causal graph from a multivariate time series x and incorporates the underlying causal mechanism into its data generation process. Distinct to the classical recurrent VAEs, our CR-VAE uses a multi-head decoder, in which the $p$-th head is responsible for generating the $p$-th dimension of $\mathbf{x}$ (i.e., $\mathbf{x}^p$). By imposing a sparsity-inducing penalty on the weights (of the decoder) and encouraging specific sets of weights to be zero, our CR-VAE learns a sparse adjacency matrix that encodes causal relations between all pairs of variables. Thanks to this causal matrix, our decoder strictly obeys the underlying principles of Granger causality, thereby making the data generating process transparent. We develop a two-stage approach to train the overall objective. Empirically, we evaluate the behavior of our model in synthetic data and two real-world human brain datasets involving, respectively, the electroencephalography (EEG) signals and the functional magnetic resonance imaging (fMRI) data. Our model consistently outperforms state-of-the-art time series generative models both qualitatively and quantitatively. Moreover, it also discovers a faithful causal graph with similar or improved accuracy over existing Granger causality-based causal inference methods. Code of CR-VAE is publicly available at https://github.com/hongmingli1995/CR-VAE.

CI-GNN: A Granger Causality-Inspired Graph Neural Network for Interpretable Brain Network-Based Psychiatric Diagnosis

There is a recent trend to leverage the power of graph neural networks (GNNs) for brain-network based psychiatric diagnosis, which,in turn, also motivates an urgent need for psychiatrists to fully understand the decision behavior of the used GNNs. However, most of the existing GNN explainers are either post-hoc in which another interpretive model needs to be created to explain a well-trained GNN, or do not consider the causal relationship between the extracted explanation and the decision, such that the explanation itself contains spurious correlations and suffers from weak faithfulness. In this work, we propose a granger causality-inspired graph neural network (CI-GNN), a built-in interpretable model that is able to identify the most influential subgraph (i.e., functional connectivity within brain regions) that is causally related to the decision (e.g., major depressive disorder patients or healthy controls), without the training of an auxillary interpretive network. CI-GNN learns disentangled subgraph-level representations {\alpha} and \b{eta} that encode, respectively, the causal and noncausal aspects of original graph under a graph variational autoencoder framework, regularized by a conditional mutual information (CMI) constraint. We theoretically justify the validity of the CMI regulation in capturing the causal relationship. We also empirically evaluate the performance of CI-GNN against three baseline GNNs and four state-of-the-art GNN explainers on synthetic data and two large-scale brain disease datasets. We observe that CI-GNN achieves the best performance in a wide range of metrics and provides more reliable and concise explanations which have clinical evidence.

Robust and Fast Measure of Information via Low-rank Representation

The matrix-based R\'enyi's entropy allows us to directly quantify information measures from given data, without explicit estimation of the underlying probability distribution. This intriguing property makes it widely applied in statistical inference and machine learning tasks. However, this information theoretical quantity is not robust against noise in the data, and is computationally prohibitive in large-scale applications. To address these issues, we propose a novel measure of information, termed low-rank matrix-based R\'enyi's entropy, based on low-rank representations of infinitely divisible kernel matrices. The proposed entropy functional inherits the specialty of of the original definition to directly quantify information from data, but enjoys additional advantages including robustness and effective calculation. Specifically, our low-rank variant is more sensitive to informative perturbations induced by changes in underlying distributions, while being insensitive to uninformative ones caused by noises. Moreover, low-rank R\'enyi's entropy can be efficiently approximated by random projection and Lanczos iteration techniques, reducing the overall complexity from $\mathcal{O}(n^3)$ to $\mathcal{O}(n^2 s)$ or even $\mathcal{O}(ns^2)$, where $n$ is the number of data samples and $s \ll n$. We conduct large-scale experiments to evaluate the effectiveness of this new information measure, demonstrating superior results compared to matrix-based R\'enyi's entropy in terms of both performance and computational efficiency.

Information-Theoretic Hashing for Zero-Shot Cross-Modal Retrieval

Zero-shot cross-modal retrieval (ZS-CMR) deals with the retrieval problem among heterogenous data from unseen classes. Typically, to guarantee generalization, the pre-defined class embeddings from natural language processing (NLP) models are used to build a common space. In this paper, instead of using an extra NLP model to define a common space beforehand, we consider a totally different way to construct (or learn) a common hamming space from an information-theoretic perspective. We term our model the Information-Theoretic Hashing (ITH), which is composed of two cascading modules: an Adaptive Information Aggregation (AIA) module; and a Semantic Preserving Encoding (SPE) module. Specifically, our AIA module takes the inspiration from the Principle of Relevant Information (PRI) to construct a common space that adaptively aggregates the intrinsic semantics of different modalities of data and filters out redundant or irrelevant information. On the other hand, our SPE module further generates the hashing codes of different modalities by preserving the similarity of intrinsic semantics with the element-wise Kullback-Leibler (KL) divergence. A total correlation regularization term is also imposed to reduce the redundancy amongst different dimensions of hash codes. Sufficient experiments on three benchmark datasets demonstrate the superiority of the proposed ITH in ZS-CMR. Source code is available in the supplementary material.

Principle of Relevant Information for Graph Sparsification

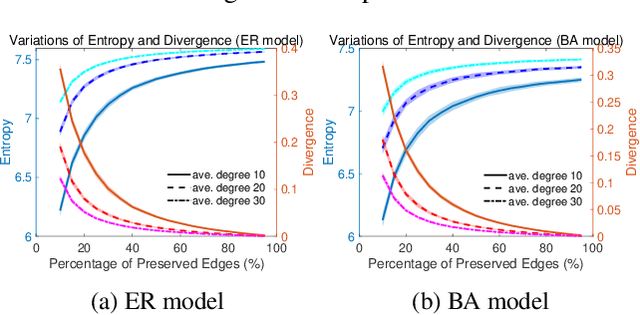
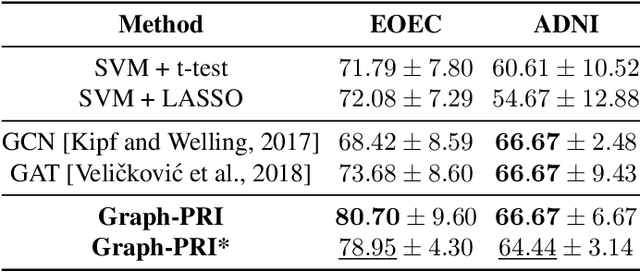
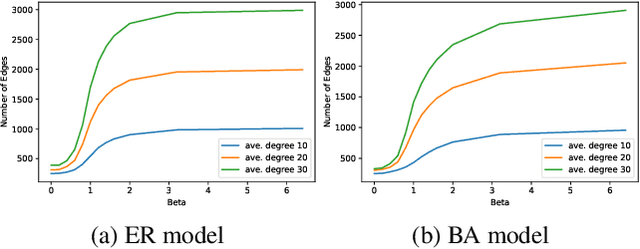
Graph sparsification aims to reduce the number of edges of a graph while maintaining its structural properties. In this paper, we propose the first general and effective information-theoretic formulation of graph sparsification, by taking inspiration from the Principle of Relevant Information (PRI). To this end, we extend the PRI from a standard scalar random variable setting to structured data (i.e., graphs). Our Graph-PRI objective is achieved by operating on the graph Laplacian, made possible by expressing the graph Laplacian of a subgraph in terms of a sparse edge selection vector $\mathbf{w}$. We provide both theoretical and empirical justifications on the validity of our Graph-PRI approach. We also analyze its analytical solutions in a few special cases. We finally present three representative real-world applications, namely graph sparsification, graph regularized multi-task learning, and medical imaging-derived brain network classification, to demonstrate the effectiveness, the versatility and the enhanced interpretability of our approach over prevalent sparsification techniques. Code of Graph-PRI is available at https://github.com/SJYuCNEL/PRI-Graphs

Optimal Randomized Approximations for Matrix based Renyi's Entropy

The Matrix-based Renyi's entropy enables us to directly measure information quantities from given data without the costly probability density estimation of underlying distributions, thus has been widely adopted in numerous statistical learning and inference tasks. However, exactly calculating this new information quantity requires access to the eigenspectrum of a semi-positive definite (SPD) matrix $A$ which grows linearly with the number of samples $n$, resulting in a $O(n^3)$ time complexity that is prohibitive for large-scale applications. To address this issue, this paper takes advantage of stochastic trace approximations for matrix-based Renyi's entropy with arbitrary $\alpha \in R^+$ orders, lowering the complexity by converting the entropy approximation to a matrix-vector multiplication problem. Specifically, we develop random approximations for integer order $\alpha$ cases and polynomial series approximations (Taylor and Chebyshev) for non-integer $\alpha$ cases, leading to a $O(n^2sm)$ overall time complexity, where $s,m \ll n$ denote the number of vector queries and the polynomial order respectively. We theoretically establish statistical guarantees for all approximation algorithms and give explicit order of s and m with respect to the approximation error $\varepsilon$, showing optimal convergence rate for both parameters up to a logarithmic factor. Large-scale simulations and real-world applications validate the effectiveness of the developed approximations, demonstrating remarkable speedup with negligible loss in accuracy.

BrainIB: Interpretable Brain Network-based Psychiatric Diagnosis with Graph Information Bottleneck

Developing a new diagnostic models based on the underlying biological mechanisms rather than subjective symptoms for psychiatric disorders is an emerging consensus. Recently, machine learning-based classifiers using functional connectivity (FC) for psychiatric disorders and healthy controls are developed to identify brain markers. However, existing machine learningbased diagnostic models are prone to over-fitting (due to insufficient training samples) and perform poorly in new test environment. Furthermore, it is difficult to obtain explainable and reliable brain biomarkers elucidating the underlying diagnostic decisions. These issues hinder their possible clinical applications. In this work, we propose BrainIB, a new graph neural network (GNN) framework to analyze functional magnetic resonance images (fMRI), by leveraging the famed Information Bottleneck (IB) principle. BrainIB is able to identify the most informative regions in the brain (i.e., subgraph) and generalizes well to unseen data. We evaluate the performance of BrainIB against 6 popular brain network classification methods on two multi-site, largescale datasets and observe that our BrainIB always achieves the highest diagnosis accuracy. It also discovers the subgraph biomarkers which are consistent to clinical and neuroimaging findings.