Shangtong Zhang
Prompt-Driven Domain Adaptation for End-to-End Autonomous Driving via In-Context RL
Nov 16, 2025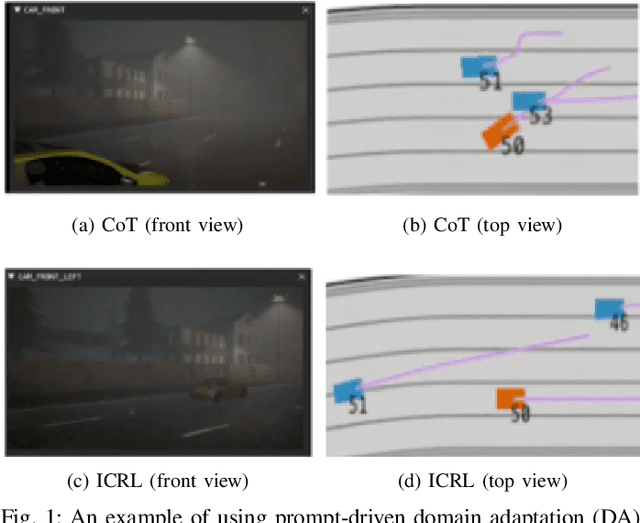
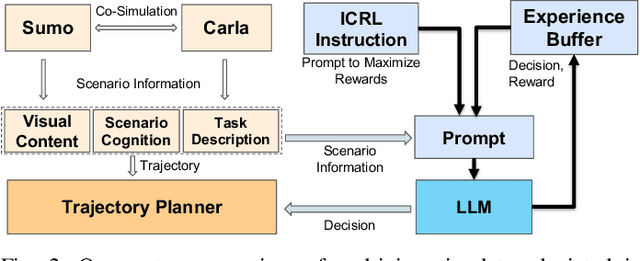

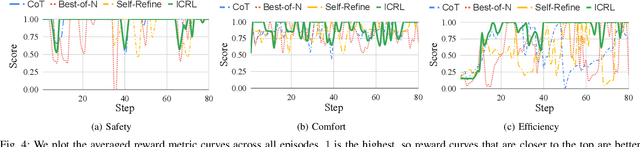
Abstract:Despite significant progress and advances in autonomous driving, many end-to-end systems still struggle with domain adaptation (DA), such as transferring a policy trained under clear weather to adverse weather conditions. Typical DA strategies in the literature include collecting additional data in the target domain or re-training the model, or both. Both these strategies quickly become impractical as we increase scale and complexity of driving. These limitations have encouraged investigation into few-shot and zero-shot prompt-driven DA at inference time involving LLMs and VLMs. These methods work by adding a few state-action trajectories during inference to the prompt (similar to in-context learning). However, there are two limitations of such an approach: $(i)$ prompt-driven DA methods are currently restricted to perception tasks such as detection and segmentation and $(ii)$ they require expert few-shot data. In this work, we present a new approach to inference-time few-shot prompt-driven DA for closed-loop autonomous driving in adverse weather condition using in-context reinforcement learning (ICRL). Similar to other prompt-driven DA methods, our approach does not require any updates to the model parameters nor does it require additional data collection in adversarial weather regime. Furthermore, our approach advances the state-of-the-art in prompt-driven DA by extending to closed driving using general trajectories observed during inference. Our experiments using the CARLA simulator show that ICRL results in safer, more efficient, and more comfortable driving policies in the target domain compared to state-of-the-art prompt-driven DA baselines.
Towards Formalizing Reinforcement Learning Theory
Nov 05, 2025Abstract:In this paper, we formalize the almost sure convergence of $Q$-learning and linear temporal difference (TD) learning with Markovian samples using the Lean 4 theorem prover based on the Mathlib library. $Q$-learning and linear TD are among the earliest and most influential reinforcement learning (RL) algorithms. The investigation of their convergence properties is not only a major research topic during the early development of the RL field but also receives increasing attention nowadays. This paper formally verifies their almost sure convergence in a unified framework based on the Robbins-Siegmund theorem. The framework developed in this work can be easily extended to convergence rates and other modes of convergence. This work thus makes an important step towards fully formalizing convergent RL results. The code is available at https://github.com/ShangtongZhang/rl-theory-in-lean.
Extensions of Robbins-Siegmund Theorem with Applications in Reinforcement Learning
Sep 30, 2025Abstract:The Robbins-Siegmund theorem establishes the convergence of stochastic processes that are almost supermartingales and is foundational for analyzing a wide range of stochastic iterative algorithms in stochastic approximation and reinforcement learning (RL). However, its original form has a significant limitation as it requires the zero-order term to be summable. In many important RL applications, this summable condition, however, cannot be met. This limitation motivates us to extend the Robbins-Siegmund theorem for almost supermartingales where the zero-order term is not summable but only square summable. Particularly, we introduce a novel and mild assumption on the increments of the stochastic processes. This together with the square summable condition enables an almost sure convergence to a bounded set. Additionally, we further provide almost sure convergence rates, high probability concentration bounds, and $L^p$ convergence rates. We then apply the new results in stochastic approximation and RL. Notably, we obtain the first almost sure convergence rate, the first high probability concentration bound, and the first $L^p$ convergence rate for $Q$-learning with linear function approximation.
Finite Sample Analysis of Linear Temporal Difference Learning with Arbitrary Features
May 27, 2025Abstract:Linear TD($\lambda$) is one of the most fundamental reinforcement learning algorithms for policy evaluation. Previously, convergence rates are typically established under the assumption of linearly independent features, which does not hold in many practical scenarios. This paper instead establishes the first $L^2$ convergence rates for linear TD($\lambda$) operating under arbitrary features, without making any algorithmic modification or additional assumptions. Our results apply to both the discounted and average-reward settings. To address the potential non-uniqueness of solutions resulting from arbitrary features, we develop a novel stochastic approximation result featuring convergence rates to the solution set instead of a single point.
Counterfactual Explanations for Continuous Action Reinforcement Learning
May 19, 2025Abstract:Reinforcement Learning (RL) has shown great promise in domains like healthcare and robotics but often struggles with adoption due to its lack of interpretability. Counterfactual explanations, which address "what if" scenarios, provide a promising avenue for understanding RL decisions but remain underexplored for continuous action spaces. We propose a novel approach for generating counterfactual explanations in continuous action RL by computing alternative action sequences that improve outcomes while minimizing deviations from the original sequence. Our approach leverages a distance metric for continuous actions and accounts for constraints such as adhering to predefined policies in specific states. Evaluations in two RL domains, Diabetes Control and Lunar Lander, demonstrate the effectiveness, efficiency, and generalization of our approach, enabling more interpretable and trustworthy RL applications.
Experience Replay Addresses Loss of Plasticity in Continual Learning
Mar 25, 2025



Abstract:Loss of plasticity is one of the main challenges in continual learning with deep neural networks, where neural networks trained via backpropagation gradually lose their ability to adapt to new tasks and perform significantly worse than their freshly initialized counterparts. The main contribution of this paper is to propose a new hypothesis that experience replay addresses the loss of plasticity in continual learning. Here, experience replay is a form of memory. We provide supporting evidence for this hypothesis. In particular, we demonstrate in multiple different tasks, including regression, classification, and policy evaluation, that by simply adding an experience replay and processing the data in the experience replay with Transformers, the loss of plasticity disappears. Notably, we do not alter any standard components of deep learning. For example, we do not change backpropagation. We do not modify the activation functions. And we do not use any regularization. We conjecture that experience replay and Transformers can address the loss of plasticity because of the in-context learning phenomenon.
GameChat: Multi-LLM Dialogue for Safe, Agile, and Socially Optimal Multi-Agent Navigation in Constrained Environments
Mar 16, 2025



Abstract:Safe, agile, and socially compliant multi-robot navigation in cluttered and constrained environments remains a critical challenge. This is especially difficult with self-interested agents in decentralized settings, where there is no central authority to resolve conflicts induced by spatial symmetry. We address this challenge by proposing a novel approach, GameChat, which facilitates safe, agile, and deadlock-free navigation for both cooperative and self-interested agents. Key to our approach is the use of natural language communication to resolve conflicts, enabling agents to prioritize more urgent tasks and break spatial symmetry in a socially optimal manner. Our algorithm ensures subgame perfect equilibrium, preventing agents from deviating from agreed-upon behaviors and supporting cooperation. Furthermore, we guarantee safety through control barrier functions and preserve agility by minimizing disruptions to agents' planned trajectories. We evaluate GameChat in simulated environments with doorways and intersections. The results show that even in the worst case, GameChat reduces the time for all agents to reach their goals by over 35% from a naive baseline and by over 20% from SMG-CBF in the intersection scenario, while doubling the rate of ensuring the agent with a higher priority task reaches the goal first, from 50% (equivalent to random chance) to a 100% perfect performance at maximizing social welfare.
Group Fairness in Multi-Task Reinforcement Learning
Mar 10, 2025



Abstract:This paper addresses a critical societal consideration in the application of Reinforcement Learning (RL): ensuring equitable outcomes across different demographic groups in multi-task settings. While previous work has explored fairness in single-task RL, many real-world applications are multi-task in nature and require policies to maintain fairness across all tasks. We introduce a novel formulation of multi-task group fairness in RL and propose a constrained optimization algorithm that explicitly enforces fairness constraints across multiple tasks simultaneously. We have shown that our proposed algorithm does not violate fairness constraints with high probability and with sublinear regret in the finite-horizon episodic setting. Through experiments in RiverSwim and MuJoCo environments, we demonstrate that our approach better ensures group fairness across multiple tasks compared to previous methods that lack explicit multi-task fairness constraints in both the finite-horizon setting and the infinite-horizon setting. Our results show that the proposed algorithm achieves smaller fairness gaps while maintaining comparable returns across different demographic groups and tasks, suggesting its potential for addressing fairness concerns in real-world multi-task RL applications.
Towards Large Language Models that Benefit for All: Benchmarking Group Fairness in Reward Models
Mar 10, 2025



Abstract:As Large Language Models (LLMs) become increasingly powerful and accessible to human users, ensuring fairness across diverse demographic groups, i.e., group fairness, is a critical ethical concern. However, current fairness and bias research in LLMs is limited in two aspects. First, compared to traditional group fairness in machine learning classification, it requires that the non-sensitive attributes, in this case, the prompt questions, be the same across different groups. In many practical scenarios, different groups, however, may prefer different prompt questions and this requirement becomes impractical. Second, it evaluates group fairness only for the LLM's final output without identifying the source of possible bias. Namely, the bias in LLM's output can result from both the pretraining and the finetuning. For finetuning, the bias can result from both the RLHF procedure and the learned reward model. Arguably, evaluating the group fairness of each component in the LLM pipeline could help develop better methods to mitigate the possible bias. Recognizing those two limitations, this work benchmarks the group fairness of learned reward models. By using expert-written text from arXiv, we are able to benchmark the group fairness of reward models without requiring the same prompt questions across different demographic groups. Surprisingly, our results demonstrate that all the evaluated reward models (e.g., Nemotron-4-340B-Reward, ArmoRM-Llama3-8B-v0.1, and GRM-llama3-8B-sftreg) exhibit statistically significant group unfairness. We also observed that top-performing reward models (w.r.t. canonical performance metrics) tend to demonstrate better group fairness.
A Survey of In-Context Reinforcement Learning
Feb 11, 2025

Abstract:Reinforcement learning (RL) agents typically optimize their policies by performing expensive backward passes to update their network parameters. However, some agents can solve new tasks without updating any parameters by simply conditioning on additional context such as their action-observation histories. This paper surveys work on such behavior, known as in-context reinforcement learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge