MathlibLemma: Folklore Lemma Generation and Benchmark for Formal Mathematics

While the ecosystem of Lean and Mathlib has enjoyed celebrated success in formal mathematical reasoning with the help of large language models (LLMs), the absence of many folklore lemmas in Mathlib remains a persistent barrier that limits Lean's usability as an everyday tool for mathematicians like LaTeX or Maple. To address this, we introduce MathlibLemma, the first LLM-based multi-agent system to automate the discovery and formalization of mathematical folklore lemmas. This framework constitutes our primary contribution, proactively mining the missing connective tissue of mathematics. Its efficacy is demonstrated by the production of a verified library of folklore lemmas, a subset of which has already been formally merged into the latest build of Mathlib, thereby validating the system's real-world utility and alignment with expert standards. Leveraging this pipeline, we further construct the MathlibLemma benchmark, a suite of 4,028 type-checked Lean statements spanning a broad range of mathematical domains. By transforming the role of LLMs from passive consumers to active contributors, this work establishes a constructive methodology for the self-evolution of formal mathematical libraries.

Prompt-Driven Domain Adaptation for End-to-End Autonomous Driving via In-Context RL

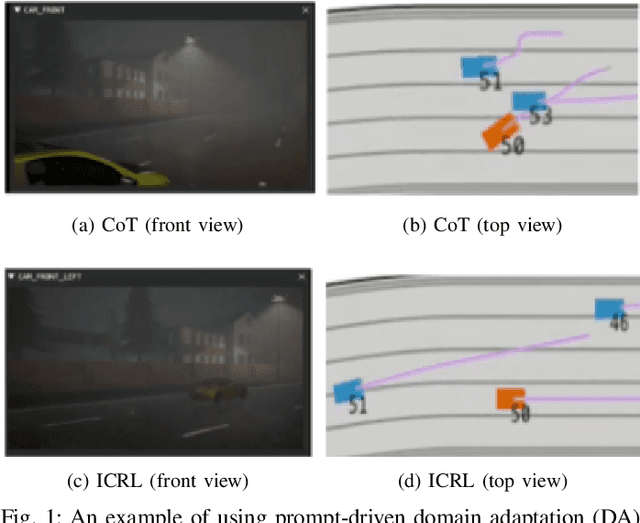
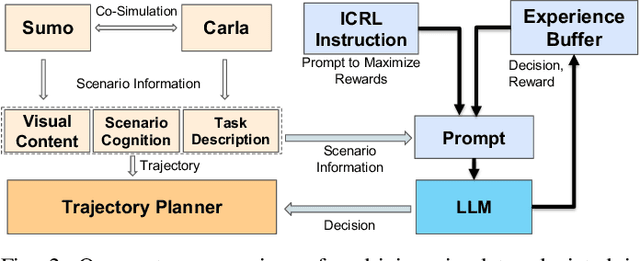
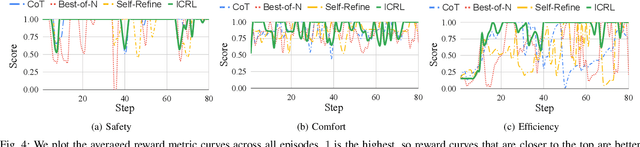
Despite significant progress and advances in autonomous driving, many end-to-end systems still struggle with domain adaptation (DA), such as transferring a policy trained under clear weather to adverse weather conditions. Typical DA strategies in the literature include collecting additional data in the target domain or re-training the model, or both. Both these strategies quickly become impractical as we increase scale and complexity of driving. These limitations have encouraged investigation into few-shot and zero-shot prompt-driven DA at inference time involving LLMs and VLMs. These methods work by adding a few state-action trajectories during inference to the prompt (similar to in-context learning). However, there are two limitations of such an approach: $(i)$ prompt-driven DA methods are currently restricted to perception tasks such as detection and segmentation and $(ii)$ they require expert few-shot data. In this work, we present a new approach to inference-time few-shot prompt-driven DA for closed-loop autonomous driving in adverse weather condition using in-context reinforcement learning (ICRL). Similar to other prompt-driven DA methods, our approach does not require any updates to the model parameters nor does it require additional data collection in adversarial weather regime. Furthermore, our approach advances the state-of-the-art in prompt-driven DA by extending to closed driving using general trajectories observed during inference. Our experiments using the CARLA simulator show that ICRL results in safer, more efficient, and more comfortable driving policies in the target domain compared to state-of-the-art prompt-driven DA baselines.

A Survey of In-Context Reinforcement Learning

Reinforcement learning (RL) agents typically optimize their policies by performing expensive backward passes to update their network parameters. However, some agents can solve new tasks without updating any parameters by simply conditioning on additional context such as their action-observation histories. This paper surveys work on such behavior, known as in-context reinforcement learning.

Mathador-LM: A Dynamic Benchmark for Mathematical Reasoning on Large Language Models

We introduce Mathador-LM, a new benchmark for evaluating the mathematical reasoning on large language models (LLMs), combining ruleset interpretation, planning, and problem-solving. This benchmark is inspired by the Mathador game, where the objective is to reach a target number using basic arithmetic operations on a given set of base numbers, following a simple set of rules. We show that, across leading LLMs, we obtain stable average performance while generating benchmark instances dynamically, following a target difficulty level. Thus, our benchmark alleviates concerns about test-set leakage into training data, an issue that often undermines popular benchmarks. Additionally, we conduct a comprehensive evaluation of both open and closed-source state-of-the-art LLMs on Mathador-LM. Our findings reveal that contemporary models struggle with Mathador-LM, scoring significantly lower than average 5th graders. This stands in stark contrast to their strong performance on popular mathematical reasoning benchmarks.