Implicit Rate-Constrained Optimization of Non-decomposable Objectives

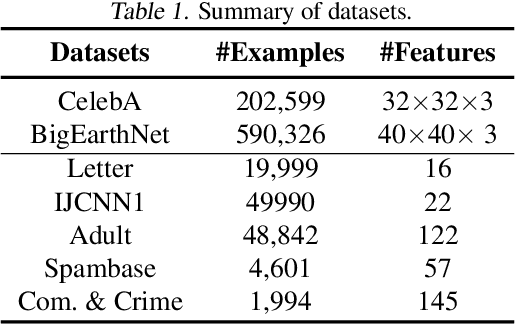
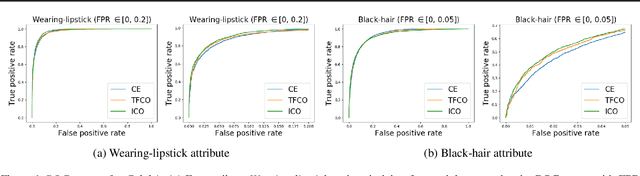
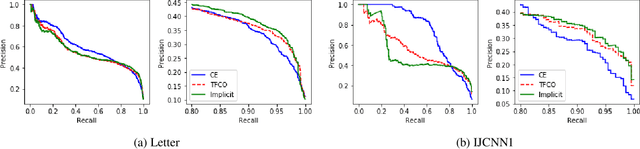
We consider a popular family of constrained optimization problems arising in machine learning that involve optimizing a non-decomposable evaluation metric with a certain thresholded form, while constraining another metric of interest. Examples of such problems include optimizing the false negative rate at a fixed false positive rate, optimizing precision at a fixed recall, optimizing the area under the precision-recall or ROC curves, etc. Our key idea is to formulate a rate-constrained optimization that expresses the threshold parameter as a function of the model parameters via the Implicit Function theorem. We show how the resulting optimization problem can be solved using standard gradient based methods. Experiments on benchmark datasets demonstrate the effectiveness of our proposed method over existing state-of-the art approaches for these problems. The code for the proposed method is available at https://github.com/google-research/google-research/tree/master/implicit_constrained_optimization .

Churn Reduction via Distillation

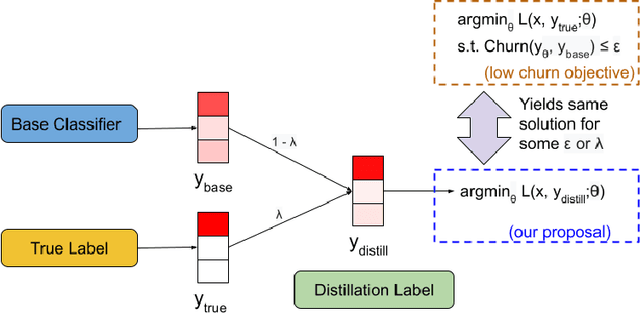
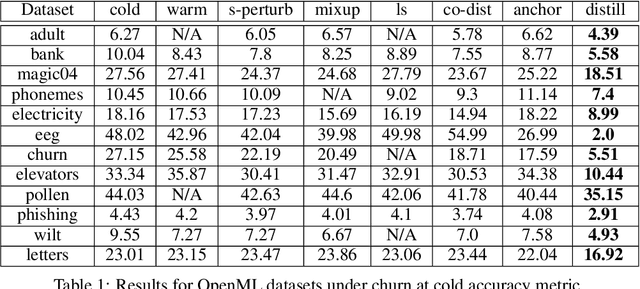
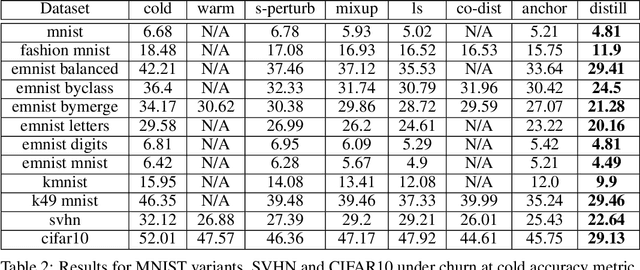
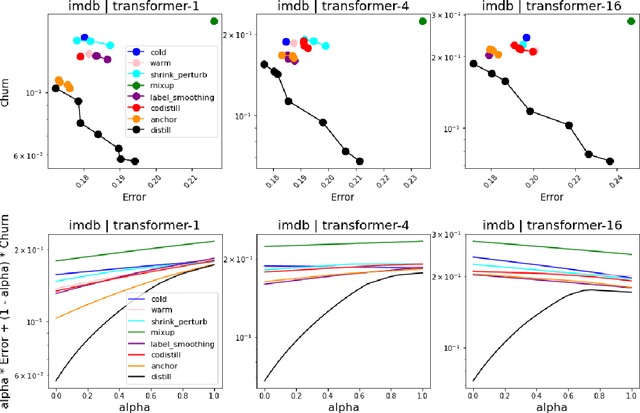
In real-world systems, models are frequently updated as more data becomes available, and in addition to achieving high accuracy, the goal is to also maintain a low difference in predictions compared to the base model (i.e. predictive ``churn''). If model retraining results in vastly different behavior, then it could cause negative effects in downstream systems, especially if this churn can be avoided with limited impact on model accuracy. In this paper, we show an equivalence between training with distillation using the base model as the teacher and training with an explicit constraint on the predictive churn. We then show that distillation performs strongly for low churn training against a number of recent baselines on a wide range of datasets and model architectures, including fully-connected networks, convolutional networks, and transformers.

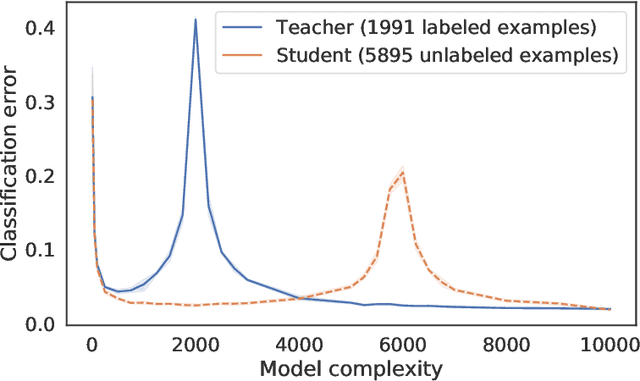
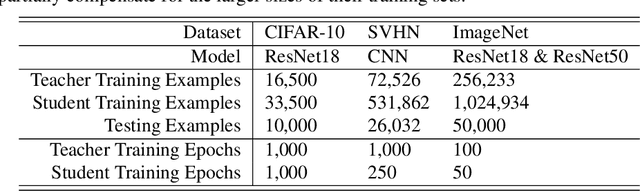
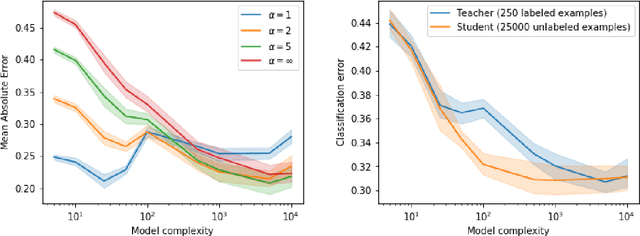
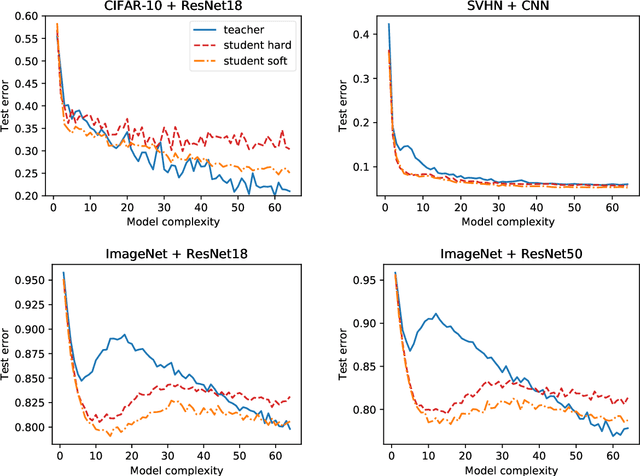
Distilling Double Descent

Distillation is the technique of training a "student" model based on examples that are labeled by a separate "teacher" model, which itself is trained on a labeled dataset. The most common explanations for why distillation "works" are predicated on the assumption that student is provided with \emph{soft} labels, \eg probabilities or confidences, from the teacher model. In this work, we show, that, even when the teacher model is highly overparameterized, and provides \emph{hard} labels, using a very large held-out unlabeled dataset to train the student model can result in a model that outperforms more "traditional" approaches. Our explanation for this phenomenon is based on recent work on "double descent". It has been observed that, once a model's complexity roughly exceeds the amount required to memorize the training data, increasing the complexity \emph{further} can, counterintuitively, result in \emph{better} generalization. Researchers have identified several settings in which it takes place, while others have made various attempts to explain it (thus far, with only partial success). In contrast, we avoid these questions, and instead seek to \emph{exploit} this phenomenon by demonstrating that a highly-overparameterized teacher can avoid overfitting via double descent, while a student trained on a larger independent dataset labeled by this teacher will avoid overfitting due to the size of its training set.

Robust Optimization for Fairness with Noisy Protected Groups

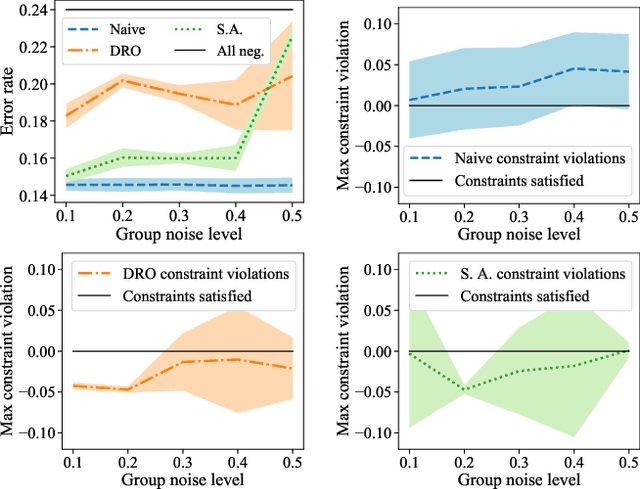
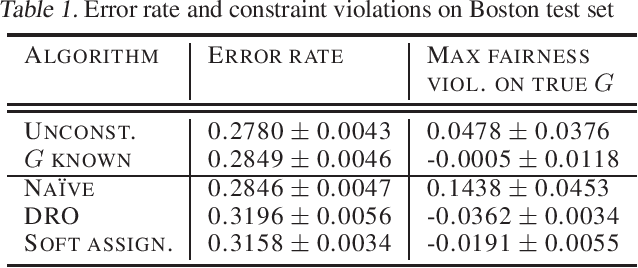
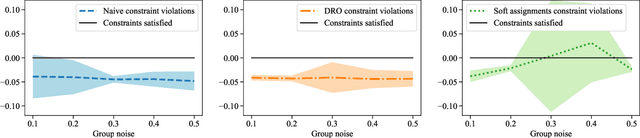
Many existing fairness criteria for machine learning involve equalizing or achieving some metric across \textit{protected groups} such as race or gender groups. However, practitioners trying to audit or enforce such group-based criteria can easily face the problem of noisy or biased protected group information. We study this important practical problem in two ways. First, we study the consequences of na{\"i}vely only relying on noisy protected groups: we provide an upper bound on the fairness violations on the true groups $G$ when the fairness criteria are satisfied on noisy groups $\hat{G}$. Second, we introduce two new approaches using robust optimization that, unlike the na{\"i}ve approach of only relying on $\hat{G}$, are guaranteed to satisfy fairness criteria on the true protected groups $G$ while minimizing a training objective. We provide theoretical guarantees that one such approach converges to an optimal feasible solution. Using two case studies, we empirically show that the robust approaches achieve better true group fairness guarantees than the na{\"i}ve approach.

Optimizing Generalized Rate Metrics through Game Equilibrium

We present a general framework for solving a large class of learning problems with non-linear functions of classification rates. This includes problems where one wishes to optimize a non-decomposable performance metric such as the F-measure or G-mean, and constrained training problems where the classifier needs to satisfy non-linear rate constraints such as predictive parity fairness, distribution divergences or churn ratios. We extend previous two-player game approaches for constrained optimization to a game between three players to decouple the classifier rates from the non-linear objective, and seek to find an equilibrium of the game. Our approach generalizes many existing algorithms, and makes possible new algorithms with more flexibility and tighter handling of non-linear rate constraints. We provide convergence guarantees for convex functions of rates, and show how our methodology can be extended to handle sums of ratios of rates. Experiments on different fairness tasks confirm the efficacy of our approach.

Pairwise Fairness for Ranking and Regression

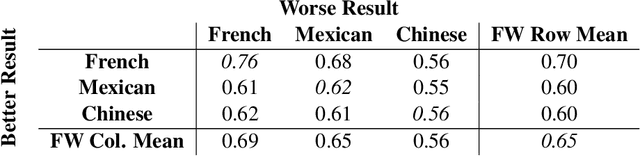
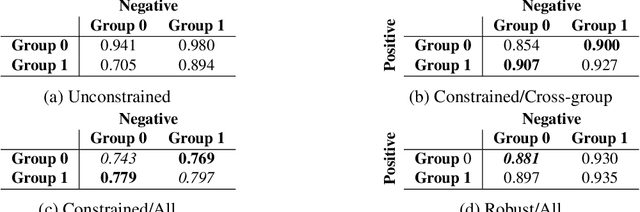
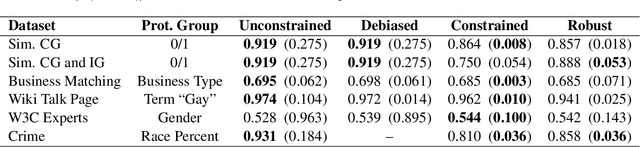
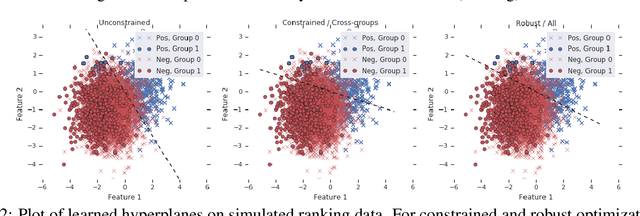
We present pairwise metrics of fairness for ranking and regression models that form analogues of statistical fairness notions such as equal opportunity or equal accuracy, as well as statistical parity. Our pairwise formulation supports both discrete protected groups, and continuous protected attributes. We show that the resulting training problems can be efficiently and effectively solved using constrained optimization and robust optimization techniques based on two player game algorithms developed for fair classification. Experiments illustrate the broad applicability and trade-offs of these methods.

Training Well-Generalizing Classifiers for Fairness Metrics and Other Data-Dependent Constraints

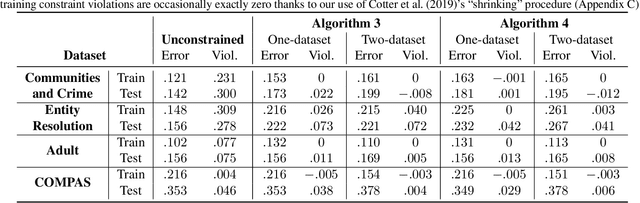
Classifiers can be trained with data-dependent constraints to satisfy fairness goals, reduce churn, achieve a targeted false positive rate, or other policy goals. We study the generalization performance for such constrained optimization problems, in terms of how well the constraints are satisfied at evaluation time, given that they are satisfied at training time. To improve generalization performance, we frame the problem as a two-player game where one player optimizes the model parameters on a training dataset, and the other player enforces the constraints on an independent validation dataset. We build on recent work in two-player constrained optimization to show that if one uses this two-dataset approach, then constraint generalization can be significantly improved. As we illustrate experimentally, this approach works not only in theory, but also in practice.

Two-Player Games for Efficient Non-Convex Constrained Optimization

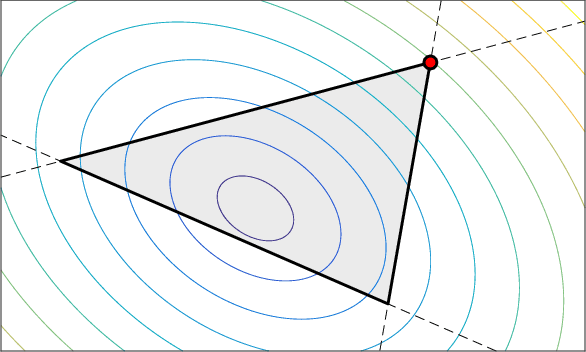
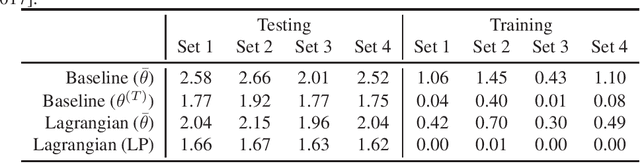
In recent years, constrained optimization has become increasingly relevant to the machine learning community, with applications including Neyman-Pearson classification, robust optimization, and fair machine learning. A natural approach to constrained optimization is to optimize the Lagrangian, but this is not guaranteed to work in the non-convex setting, and, if using a first-order method, cannot cope with non-differentiable constraints (e.g. constraints on rates or proportions). The Lagrangian can be interpreted as a two-player game played between a player who seeks to optimize over the model parameters, and a player who wishes to maximize over the Lagrange multipliers. We propose a non-zero-sum variant of the Lagrangian formulation that can cope with non-differentiable--even discontinuous--constraints, which we call the "proxy-Lagrangian". The first player minimizes external regret in terms of easy-to-optimize "proxy constraints", while the second player enforces the original constraints by minimizing swap regret. For this new formulation, as for the Lagrangian in the non-convex setting, the result is a stochastic classifier. For both the proxy-Lagrangian and Lagrangian formulations, however, we prove that this classifier, instead of having unbounded size, can be taken to be a distribution over no more than m+1 models (where m is the number of constraints). This is a significant improvement in practical terms.

Optimization with Non-Differentiable Constraints with Applications to Fairness, Recall, Churn, and Other Goals

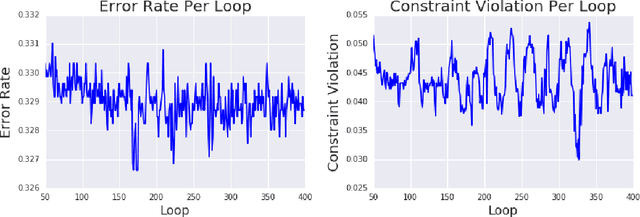
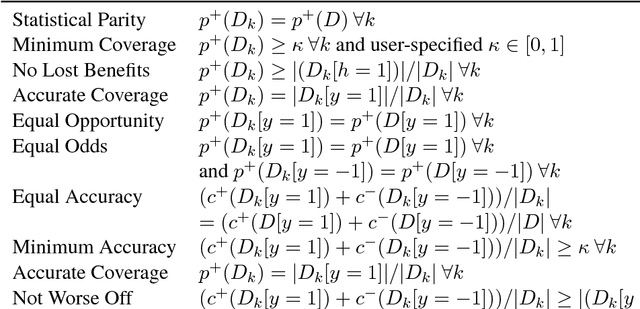
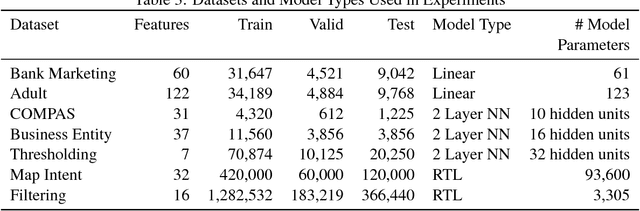
We show that many machine learning goals, such as improved fairness metrics, can be expressed as constraints on the model's predictions, which we call rate constraints. We study the problem of training non-convex models subject to these rate constraints (or any non-convex and non-differentiable constraints). In the non-convex setting, the standard approach of Lagrange multipliers may fail. Furthermore, if the constraints are non-differentiable, then one cannot optimize the Lagrangian with gradient-based methods. To solve these issues, we introduce the proxy-Lagrangian formulation. This new formulation leads to an algorithm that produces a stochastic classifier by playing a two-player non-zero-sum game solving for what we call a semi-coarse correlated equilibrium, which in turn corresponds to an approximately optimal and feasible solution to the constrained optimization problem. We then give a procedure which shrinks the randomized solution down to one that is a mixture of at most $m+1$ deterministic solutions, given $m$ constraints. This culminates in algorithms that can solve non-convex constrained optimization problems with possibly non-differentiable and non-convex constraints with theoretical guarantees. We provide extensive experimental results enforcing a wide range of policy goals including different fairness metrics, and other goals on accuracy, coverage, recall, and churn.

Proxy Fairness

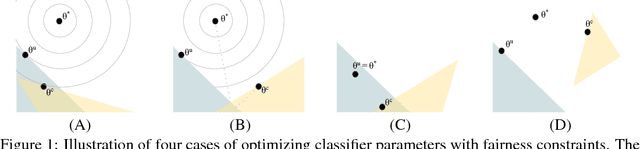
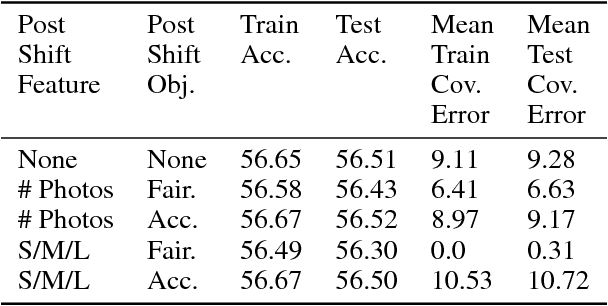
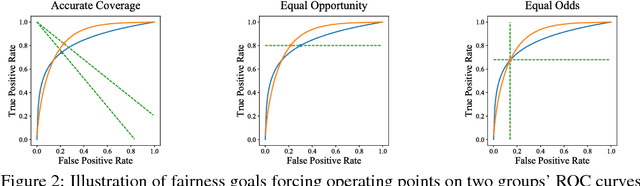
We consider the problem of improving fairness when one lacks access to a dataset labeled with protected groups, making it difficult to take advantage of strategies that can improve fairness but require protected group labels, either at training or runtime. To address this, we investigate improving fairness metrics for proxy groups, and test whether doing so results in improved fairness for the true sensitive groups. Results on benchmark and real-world datasets demonstrate that such a proxy fairness strategy can work well in practice. However, we caution that the effectiveness likely depends on the choice of fairness metric, as well as how aligned the proxy groups are with the true protected groups in terms of the constrained model parameters.