Informed Correctors for Discrete Diffusion Models

Discrete diffusion modeling is a promising framework for modeling and generating data in discrete spaces. To sample from these models, different strategies present trade-offs between computation and sample quality. A predominant sampling strategy is predictor-corrector $\tau$-leaping, which simulates the continuous time generative process with discretized predictor steps and counteracts the accumulation of discretization error via corrector steps. However, for absorbing state diffusion, an important class of discrete diffusion models, the standard forward-backward corrector can be ineffective in fixing such errors, resulting in subpar sample quality. To remedy this problem, we propose a family of informed correctors that more reliably counteracts discretization error by leveraging information learned by the model. For further efficiency gains, we also propose $k$-Gillespie's, a sampling algorithm that better utilizes each model evaluation, while still enjoying the speed and flexibility of $\tau$-leaping. Across several real and synthetic datasets, we show that $k$-Gillespie's with informed correctors reliably produces higher quality samples at lower computational cost.

Modeling Latent Neural Dynamics with Gaussian Process Switching Linear Dynamical Systems

Understanding how the collective activity of neural populations relates to computation and ultimately behavior is a key goal in neuroscience. To this end, statistical methods which describe high-dimensional neural time series in terms of low-dimensional latent dynamics have played a fundamental role in characterizing neural systems. Yet, what constitutes a successful method involves two opposing criteria: (1) methods should be expressive enough to capture complex nonlinear dynamics, and (2) they should maintain a notion of interpretability often only warranted by simpler linear models. In this paper, we develop an approach that balances these two objectives: the Gaussian Process Switching Linear Dynamical System (gpSLDS). Our method builds on previous work modeling the latent state evolution via a stochastic differential equation whose nonlinear dynamics are described by a Gaussian process (GP-SDEs). We propose a novel kernel function which enforces smoothly interpolated locally linear dynamics, and therefore expresses flexible -- yet interpretable -- dynamics akin to those of recurrent switching linear dynamical systems (rSLDS). Our approach resolves key limitations of the rSLDS such as artifactual oscillations in dynamics near discrete state boundaries, while also providing posterior uncertainty estimates of the dynamics. To fit our models, we leverage a modified learning objective which improves the estimation accuracy of kernel hyperparameters compared to previous GP-SDE fitting approaches. We apply our method to synthetic data and data recorded in two neuroscience experiments and demonstrate favorable performance in comparison to the rSLDS.

Inferring Inference

Patterns of microcircuitry suggest that the brain has an array of repeated canonical computational units. Yet neural representations are distributed, so the relevant computations may only be related indirectly to single-neuron transformations. It thus remains an open challenge how to define canonical distributed computations. We integrate normative and algorithmic theories of neural computation into a mathematical framework for inferring canonical distributed computations from large-scale neural activity patterns. At the normative level, we hypothesize that the brain creates a structured internal model of its environment, positing latent causes that explain its sensory inputs, and uses those sensory inputs to infer the latent causes. At the algorithmic level, we propose that this inference process is a nonlinear message-passing algorithm on a graph-structured model of the world. Given a time series of neural activity during a perceptual inference task, our framework finds (i) the neural representation of relevant latent variables, (ii) interactions between these variables that define the brain's internal model of the world, and (iii) message-functions specifying the inference algorithm. These targeted computational properties are then statistically distinguishable due to the symmetries inherent in any canonical computation, up to a global transformation. As a demonstration, we simulate recordings for a model brain that implicitly implements an approximate inference algorithm on a probabilistic graphical model. Given its external inputs and noisy neural activity, we recover the latent variables, their neural representation and dynamics, and canonical message-functions. We highlight features of experimental design needed to successfully extract canonical computations from neural data. Overall, this framework provides a new tool for discovering interpretable structure in neural recordings.

NAS-X: Neural Adaptive Smoothing via Twisting

We present Neural Adaptive Smoothing via Twisting (NAS-X), a method for learning and inference in sequential latent variable models based on reweighted wake-sleep (RWS). NAS-X works with both discrete and continuous latent variables, and leverages smoothing SMC to fit a broader range of models than traditional RWS methods. We test NAS-X on discrete and continuous tasks and find that it substantially outperforms previous variational and RWS-based methods in inference and parameter recovery.

SIXO: Smoothing Inference with Twisted Objectives

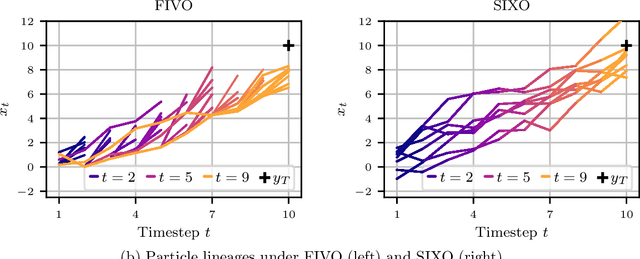
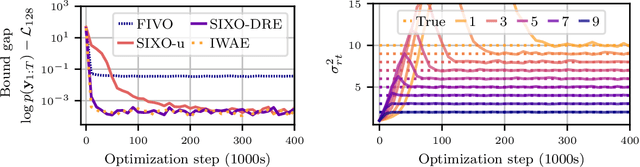
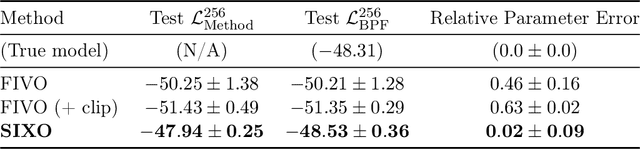
Sequential Monte Carlo (SMC) is an inference algorithm for state space models that approximates the posterior by sampling from a sequence of target distributions. The target distributions are often chosen to be the filtering distributions, but these ignore information from future observations, leading to practical and theoretical limitations in inference and model learning. We introduce SIXO, a method that instead learns targets that approximate the smoothing distributions, incorporating information from all observations. The key idea is to use density ratio estimation to fit functions that warp the filtering distributions into the smoothing distributions. We then use SMC with these learned targets to define a variational objective for model and proposal learning. SIXO yields provably tighter log marginal lower bounds and offers significantly more accurate posterior inferences and parameter estimates in a variety of domains.

Streaming Inference for Infinite Non-Stationary Clustering

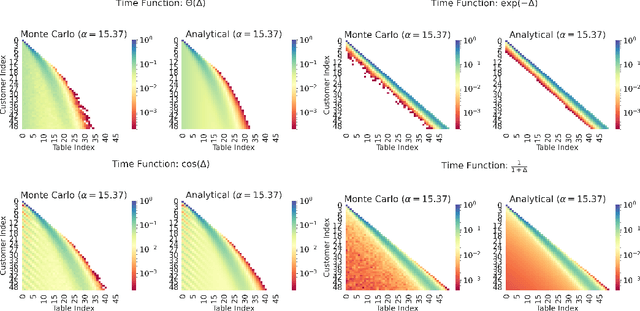
Learning from a continuous stream of non-stationary data in an unsupervised manner is arguably one of the most common and most challenging settings facing intelligent agents. Here, we attack learning under all three conditions (unsupervised, streaming, non-stationary) in the context of clustering, also known as mixture modeling. We introduce a novel clustering algorithm that endows mixture models with the ability to create new clusters online, as demanded by the data, in a probabilistic, time-varying, and principled manner. To achieve this, we first define a novel stochastic process called the Dynamical Chinese Restaurant Process (Dynamical CRP), which is a non-exchangeable distribution over partitions of a set; next, we show that the Dynamical CRP provides a non-stationary prior over cluster assignments and yields an efficient streaming variational inference algorithm. We conclude with experiments showing that the Dynamical CRP can be applied on diverse synthetic and real data with Gaussian and non-Gaussian likelihoods.

Bayesian recurrent state space model for rs-fMRI

We propose a hierarchical Bayesian recurrent state space model for modeling switching network connectivity in resting state fMRI data. Our model allows us to uncover shared network patterns across disease conditions. We evaluate our method on the ADNI2 dataset by inferring latent state patterns corresponding to altered neural circuits in individuals with Mild Cognitive Impairment (MCI). In addition to states shared across healthy and individuals with MCI, we discover latent states that are predominantly observed in individuals with MCI. Our model outperforms current state of the art deep learning method on ADNI2 dataset.

Learning Latent Permutations with Gumbel-Sinkhorn Networks

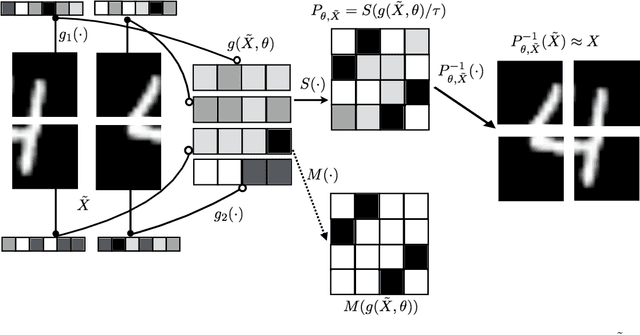
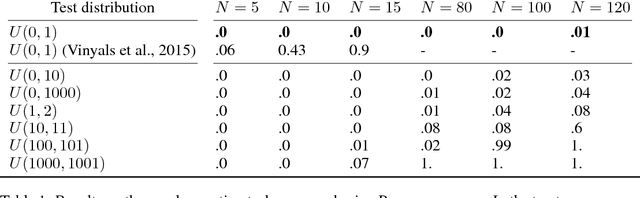
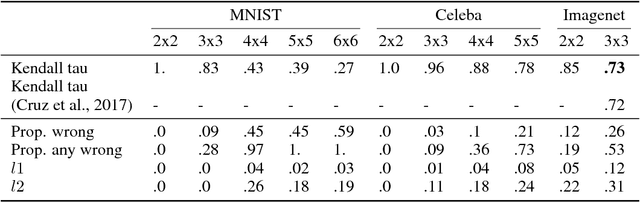
Permutations and matchings are core building blocks in a variety of latent variable models, as they allow us to align, canonicalize, and sort data. Learning in such models is difficult, however, because exact marginalization over these combinatorial objects is intractable. In response, this paper introduces a collection of new methods for end-to-end learning in such models that approximate discrete maximum-weight matching using the continuous Sinkhorn operator. Sinkhorn iteration is attractive because it functions as a simple, easy-to-implement analog of the softmax operator. With this, we can define the Gumbel-Sinkhorn method, an extension of the Gumbel-Softmax method (Jang et al. 2016, Maddison2016 et al. 2016) to distributions over latent matchings. We demonstrate the effectiveness of our method by outperforming competitive baselines on a range of qualitatively different tasks: sorting numbers, solving jigsaw puzzles, and identifying neural signals in worms.