Separating the what and how of compositional computation to enable reuse and continual learning

The ability to continually learn, retain and deploy skills to accomplish goals is a key feature of intelligent and efficient behavior. However, the neural mechanisms facilitating the continual learning and flexible (re-)composition of skills remain elusive. Here, we study continual learning and the compositional reuse of learned computations in recurrent neural network (RNN) models using a novel two-system approach: one system that infers what computation to perform, and one that implements how to perform it. We focus on a set of compositional cognitive tasks commonly studied in neuroscience. To construct the what system, we first show that a large family of tasks can be systematically described by a probabilistic generative model, where compositionality stems from a shared underlying vocabulary of discrete task epochs. The shared epoch structure makes these tasks inherently compositional. We first show that this compositionality can be systematically described by a probabilistic generative model. Furthermore, We develop an unsupervised online learning approach that can learn this model on a single-trial basis, building its vocabulary incrementally as it is exposed to new tasks, and inferring the latent epoch structure as a time-varying computational context within a trial. We implement the how system as an RNN whose low-rank components are composed according to the context inferred by the what system. Contextual inference facilitates the creation, learning, and reuse of low-rank RNN components as new tasks are introduced sequentially, enabling continual learning without catastrophic forgetting. Using an example task set, we demonstrate the efficacy and competitive performance of this two-system learning framework, its potential for forward and backward transfer, as well as fast compositional generalization to unseen tasks.

Modeling Latent Neural Dynamics with Gaussian Process Switching Linear Dynamical Systems

Understanding how the collective activity of neural populations relates to computation and ultimately behavior is a key goal in neuroscience. To this end, statistical methods which describe high-dimensional neural time series in terms of low-dimensional latent dynamics have played a fundamental role in characterizing neural systems. Yet, what constitutes a successful method involves two opposing criteria: (1) methods should be expressive enough to capture complex nonlinear dynamics, and (2) they should maintain a notion of interpretability often only warranted by simpler linear models. In this paper, we develop an approach that balances these two objectives: the Gaussian Process Switching Linear Dynamical System (gpSLDS). Our method builds on previous work modeling the latent state evolution via a stochastic differential equation whose nonlinear dynamics are described by a Gaussian process (GP-SDEs). We propose a novel kernel function which enforces smoothly interpolated locally linear dynamics, and therefore expresses flexible -- yet interpretable -- dynamics akin to those of recurrent switching linear dynamical systems (rSLDS). Our approach resolves key limitations of the rSLDS such as artifactual oscillations in dynamics near discrete state boundaries, while also providing posterior uncertainty estimates of the dynamics. To fit our models, we leverage a modified learning objective which improves the estimation accuracy of kernel hyperparameters compared to previous GP-SDE fitting approaches. We apply our method to synthetic data and data recorded in two neuroscience experiments and demonstrate favorable performance in comparison to the rSLDS.

Learning interpretable continuous-time models of latent stochastic dynamical systems

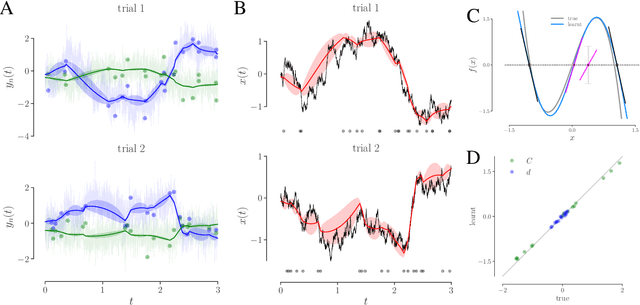
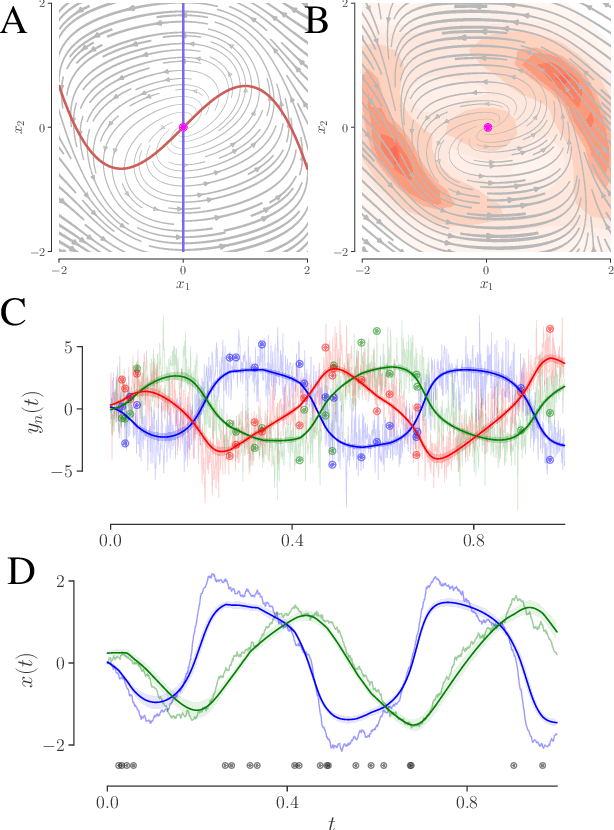
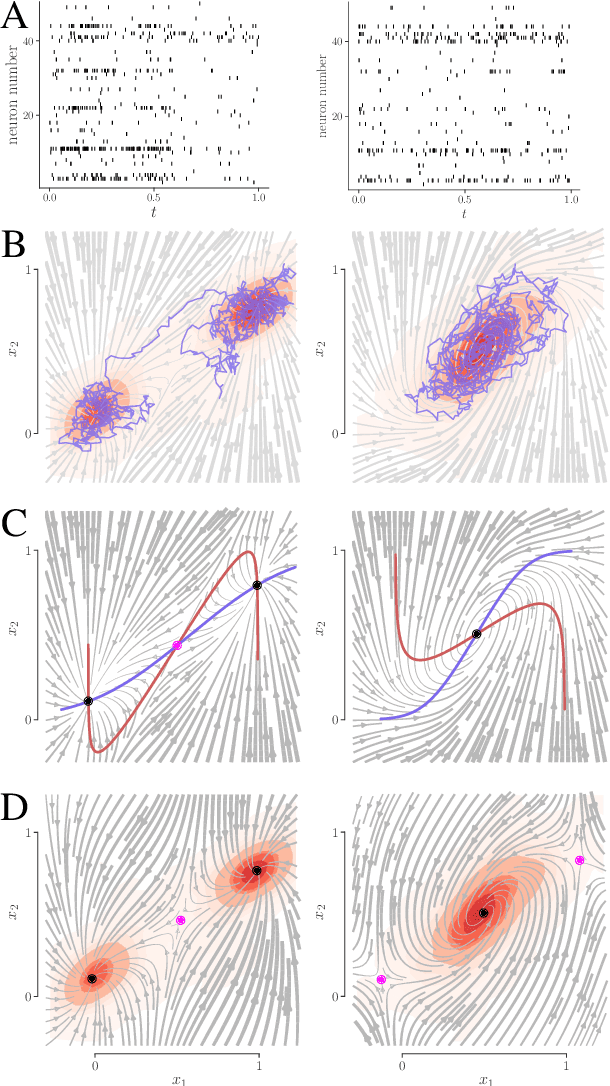
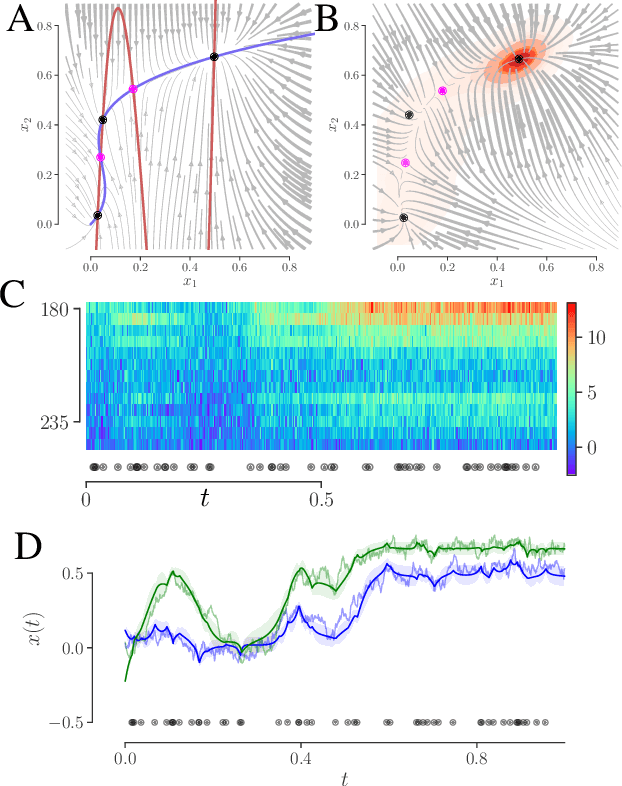
We develop an approach to learn an interpretable semi-parametric model of a latent continuous-time stochastic dynamical system, assuming noisy high-dimensional outputs sampled at uneven times. The dynamics are described by a nonlinear stochastic differential equation (SDE) driven by a Wiener process, with a drift evolution function drawn from a Gaussian process (GP) conditioned on a set of learnt fixed points and corresponding local Jacobian matrices. This form yields a flexible nonparametric model of the dynamics, with a representation corresponding directly to the interpretable portraits routinely employed in the study of nonlinear dynamical systems. The learning algorithm combines inference of continuous latent paths underlying observed data with a sparse variational description of the dynamical process. We demonstrate our approach on simulated data from different nonlinear dynamical systems.