Sanjiv Kumar
Google Research
Low-Rank Bottleneck in Multi-head Attention Models
Feb 17, 2020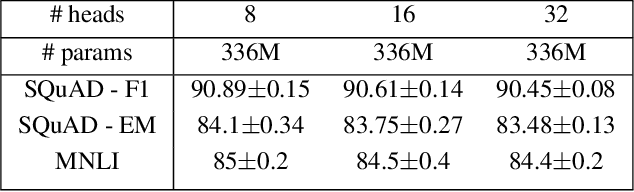
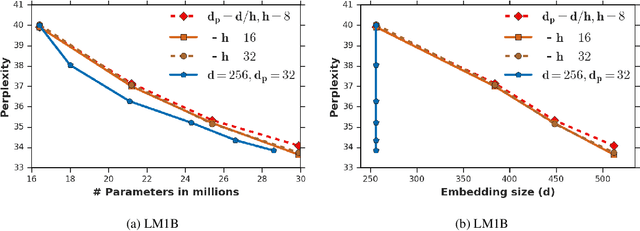
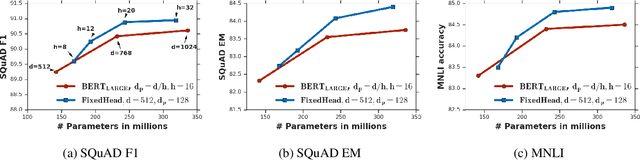
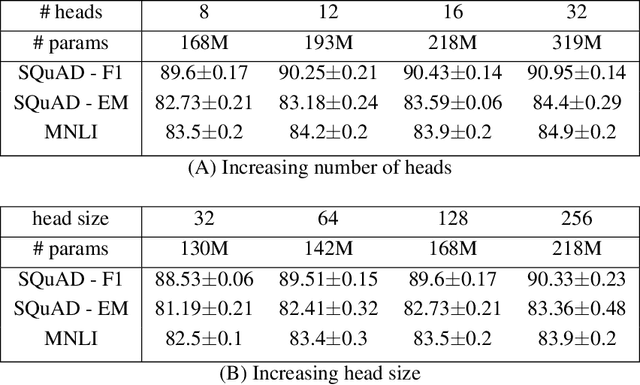
Abstract:Attention based Transformer architecture has enabled significant advances in the field of natural language processing. In addition to new pre-training techniques, recent improvements crucially rely on working with a relatively larger embedding dimension for tokens. Unfortunately, this leads to models that are prohibitively large to be employed in the downstream tasks. In this paper we identify one of the important factors contributing to the large embedding size requirement. In particular, our analysis highlights that the scaling between the number of heads and the size of each head in the current architecture gives rise to a low-rank bottleneck in attention heads, causing this limitation. We further validate this in our experiments. As a solution we propose to set the head size of an attention unit to input sequence length, and independent of the number of heads, resulting in multi-head attention layers with provably more expressive power. We empirically show that this allows us to train models with a relatively smaller embedding dimension and with better performance scaling.
Pre-training Tasks for Embedding-based Large-scale Retrieval
Feb 10, 2020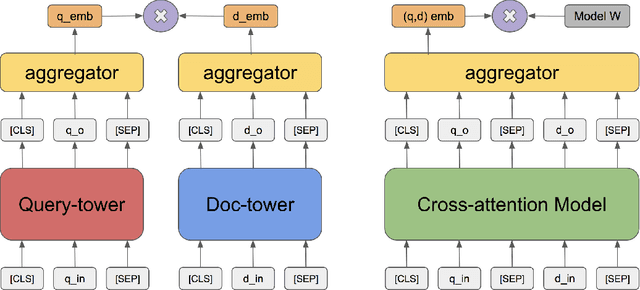
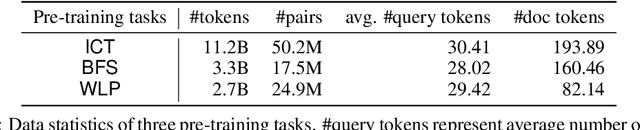

Abstract:We consider the large-scale query-document retrieval problem: given a query (e.g., a question), return the set of relevant documents (e.g., paragraphs containing the answer) from a large document corpus. This problem is often solved in two steps. The retrieval phase first reduces the solution space, returning a subset of candidate documents. The scoring phase then re-ranks the documents. Critically, the retrieval algorithm not only desires high recall but also requires to be highly efficient, returning candidates in time sublinear to the number of documents. Unlike the scoring phase witnessing significant advances recently due to the BERT-style pre-training tasks on cross-attention models, the retrieval phase remains less well studied. Most previous works rely on classic Information Retrieval (IR) methods such as BM-25 (token matching + TF-IDF weights). These models only accept sparse handcrafted features and can not be optimized for different downstream tasks of interest. In this paper, we conduct a comprehensive study on the embedding-based retrieval models. We show that the key ingredient of learning a strong embedding-based Transformer model is the set of pre-training tasks. With adequately designed paragraph-level pre-training tasks, the Transformer models can remarkably improve over the widely-used BM-25 as well as embedding models without Transformers. The paragraph-level pre-training tasks we studied are Inverse Cloze Task (ICT), Body First Selection (BFS), Wiki Link Prediction (WLP), and the combination of all three.
Are Transformers universal approximators of sequence-to-sequence functions?
Dec 20, 2019

Abstract:Despite the widespread adoption of Transformer models for NLP tasks, the expressive power of these models is not well-understood. In this paper, we establish that Transformer models are universal approximators of continuous permutation equivariant sequence-to-sequence functions with compact support, which is quite surprising given the amount of shared parameters in these models. Furthermore, using positional encodings, we circumvent the restriction of permutation equivariance, and show that Transformer models can universally approximate arbitrary continuous sequence-to-sequence functions on a compact domain. Interestingly, our proof techniques clearly highlight the different roles of the self-attention and the feed-forward layers in Transformers. In particular, we prove that fixed width self-attention layers can compute contextual mappings of the input sequences, playing a key role in the universal approximation property of Transformers. Based on this insight from our analysis, we consider other simpler alternatives to self-attention layers and empirically evaluate them.
Why ADAM Beats SGD for Attention Models
Dec 06, 2019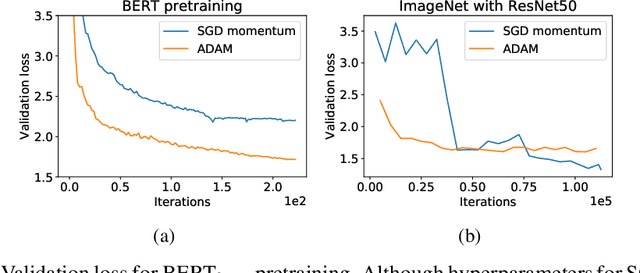

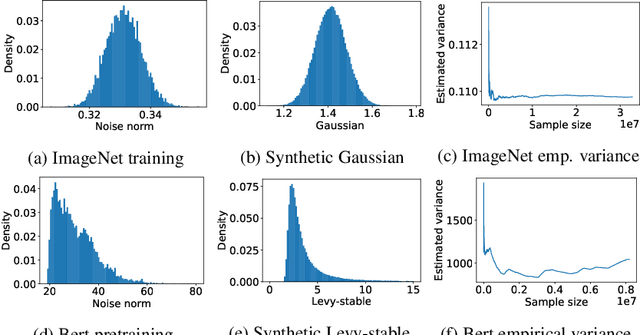

Abstract:While stochastic gradient descent (SGD) is still the de facto algorithm in deep learning, adaptive methods like Adam have been observed to outperform SGD across important tasks, such as attention models. The settings under which SGD performs poorly in comparison to Adam are not well understood yet. In this paper, we provide empirical and theoretical evidence that a heavy-tailed distribution of the noise in stochastic gradients is a root cause of SGD's poor performance. Based on this observation, we study clipped variants of SGD that circumvent this issue; we then analyze their convergence under heavy-tailed noise. Furthermore, we develop a new adaptive coordinate-wise clipping algorithm (ACClip) tailored to such settings. Subsequently, we show how adaptive methods like Adam can be viewed through the lens of clipping, which helps us explain Adam's strong performance under heavy-tail noise settings. Finally, we show that the proposed ACClip outperforms Adam for both BERT pretraining and finetuning tasks.
Learning to Learn by Zeroth-Order Oracle
Oct 21, 2019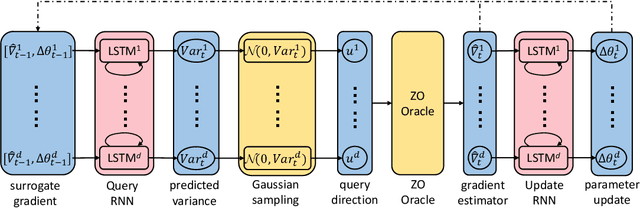

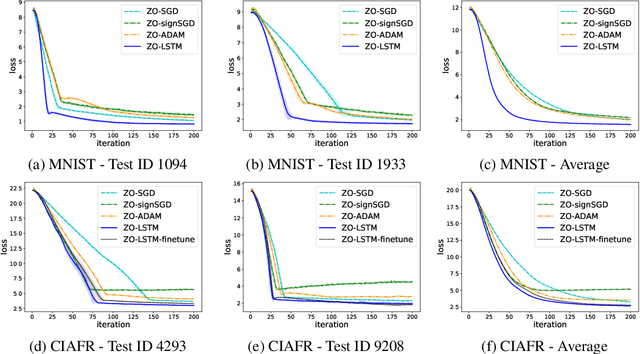
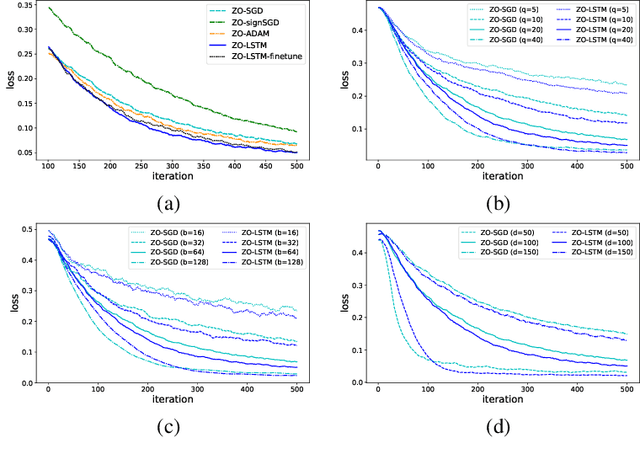
Abstract:In the learning to learn (L2L) framework, we cast the design of optimization algorithms as a machine learning problem and use deep neural networks to learn the update rules. In this paper, we extend the L2L framework to zeroth-order (ZO) optimization setting, where no explicit gradient information is available. Our learned optimizer, modeled as recurrent neural network (RNN), first approximates gradient by ZO gradient estimator and then produces parameter update utilizing the knowledge of previous iterations. To reduce high variance effect due to ZO gradient estimator, we further introduce another RNN to learn the Gaussian sampling rule and dynamically guide the query direction sampling. Our learned optimizer outperforms hand-designed algorithms in terms of convergence rate and final solution on both synthetic and practical ZO optimization tasks (in particular, the black-box adversarial attack task, which is one of the most widely used tasks of ZO optimization). We finally conduct extensive analytical experiments to demonstrate the effectiveness of our proposed optimizer.
Online Hierarchical Clustering Approximations
Sep 20, 2019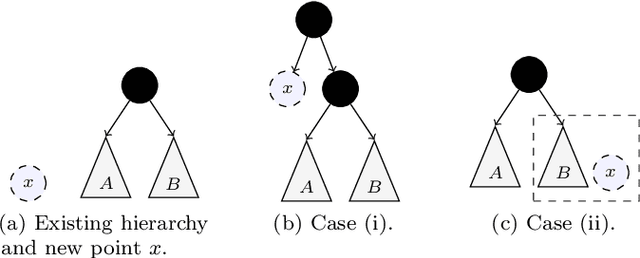

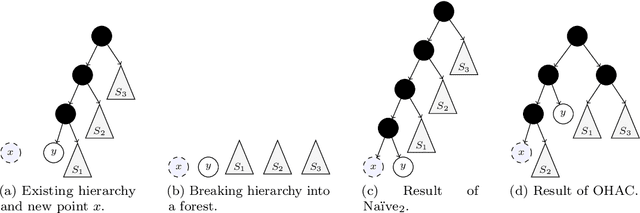
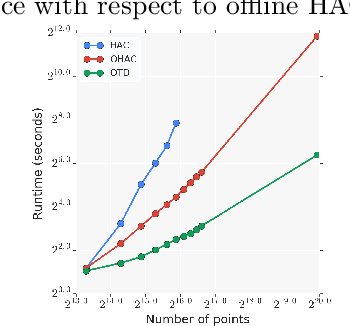
Abstract:Hierarchical clustering is a widely used approach for clustering datasets at multiple levels of granularity. Despite its popularity, existing algorithms such as hierarchical agglomerative clustering (HAC) are limited to the offline setting, and thus require the entire dataset to be available. This prohibits their use on large datasets commonly encountered in modern learning applications. In this paper, we consider hierarchical clustering in the online setting, where points arrive one at a time. We propose two algorithms that seek to optimize the Moseley and Wang (MW) revenue function, a variant of the Dasgupta cost. These algorithms offer different tradeoffs between efficiency and MW revenue performance. The first algorithm, OTD, is a highly efficient Online Top Down algorithm which provably achieves a 1/3-approximation to the MW revenue under a data separation assumption. The second algorithm, OHAC, is an online counterpart to offline HAC, which is known to yield a 1/3-approximation to the MW revenue, and produce good quality clusters in practice. We show that OHAC approximates offline HAC by leveraging a novel split-merge procedure. We empirically show that OTD and OHAC offer significant efficiency and cluster quality gains respectively over baselines.
New Loss Functions for Fast Maximum Inner Product Search
Sep 11, 2019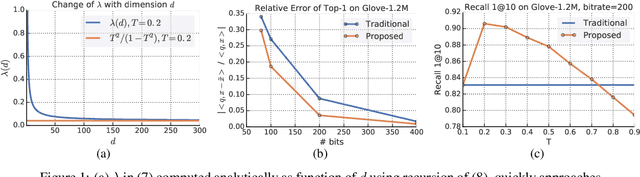
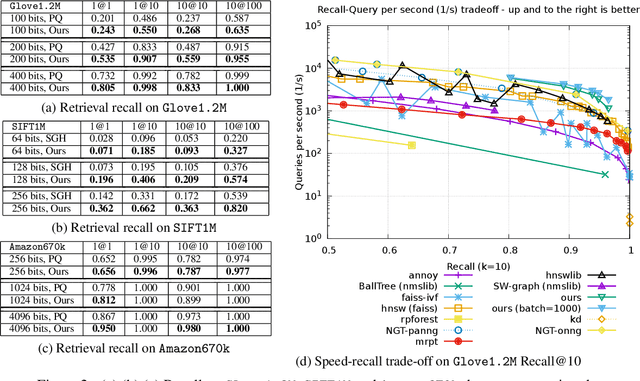
Abstract:Quantization based methods are popular for solving large scale maximum inner product search problems. However, in most traditional quantization works, the objective is to minimize the reconstruction error for datapoints to be searched. In this work, we focus directly on minimizing error in inner product approximation and derive a new class of quantization loss functions. One key aspect of the new loss functions is that we weight the error term based on the value of the inner product, giving more importance to pairs of queries and datapoints whose inner products are high. We provide theoretical grounding to the new quantization loss function, which is simple, intuitive and able to work with a variety of quantization techniques, including binary quantization and product quantization. We conduct experiments on standard benchmarking datasets to demonstrate that our method using the new objective outperforms other state-of-the-art methods.
AdaCliP: Adaptive Clipping for Private SGD
Aug 20, 2019
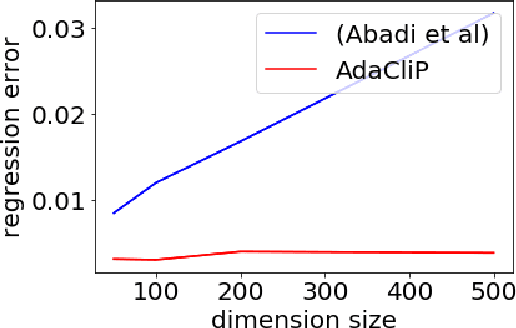
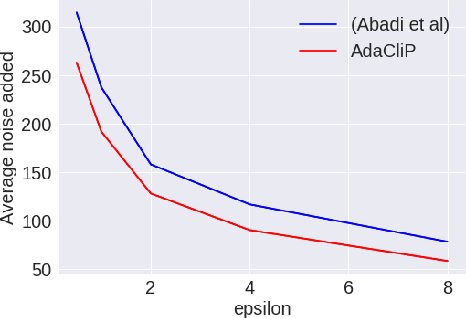

Abstract:Privacy preserving machine learning algorithms are crucial for learning models over user data to protect sensitive information. Motivated by this, differentially private stochastic gradient descent (SGD) algorithms for training machine learning models have been proposed. At each step, these algorithms modify the gradients and add noise proportional to the sensitivity of the modified gradients. Under this framework, we propose AdaCliP, a theoretically motivated differentially private SGD algorithm that provably adds less noise compared to the previous methods, by using coordinate-wise adaptive clipping of the gradient. We empirically demonstrate that AdaCliP reduces the amount of added noise and produces models with better accuracy.
Sampled Softmax with Random Fourier Features
Jul 24, 2019
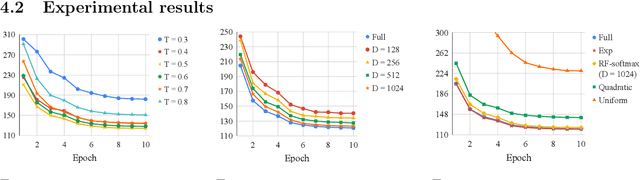

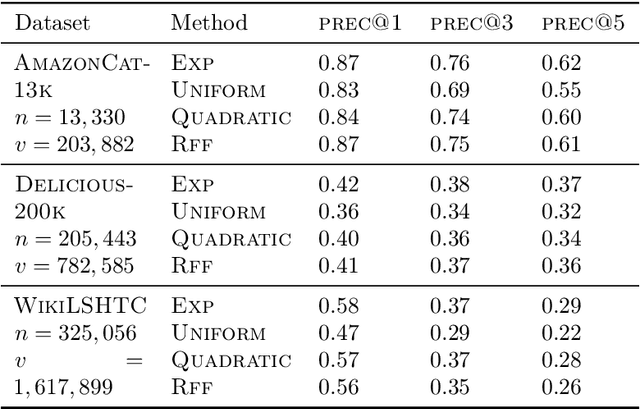
Abstract:The computational cost of training with softmax cross entropy loss grows linearly with the number of classes. For the settings where a large number of classes are involved, a common method to speed up training is to sample a subset of classes and utilize an estimate of the gradient based on these classes, known as the sampled softmax method. However, the sampled softmax provides a biased estimate of the gradient unless the samples are drawn from the exact softmax distribution, which is again expensive to compute. Therefore, a widely employed practical approach (without theoretical justification) involves sampling from a simpler distribution in the hope of approximating the exact softmax distribution. In this paper, we develop the first theoretical understanding of the role that different sampling distributions play in determining the quality of sampled softmax. Motivated by our analysis and the work on kernel-based sampling, we propose the Random Fourier Softmax (RF-softmax) method that utilizes the powerful Random Fourier features to enable more efficient and accurate sampling from the (approximate) softmax distribution. We show that RF-softmax leads to low bias in estimation in terms of both the full softmax distribution and the full softmax gradient. Furthermore, the cost of RF-softmax scales only logarithmically with the number of classes.
Neural SDE: Stabilizing Neural ODE Networks with Stochastic Noise
Jun 05, 2019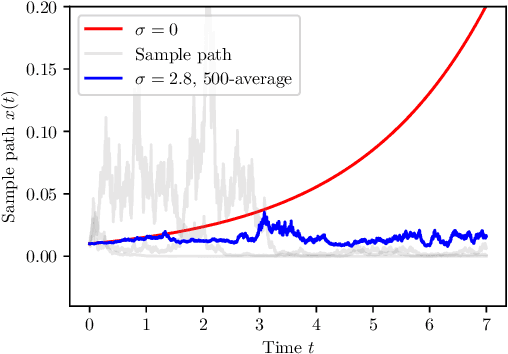

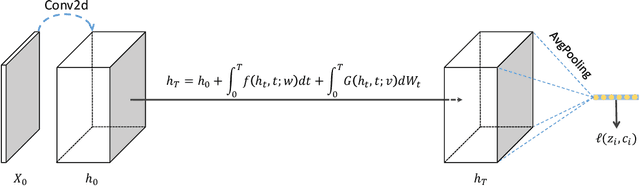
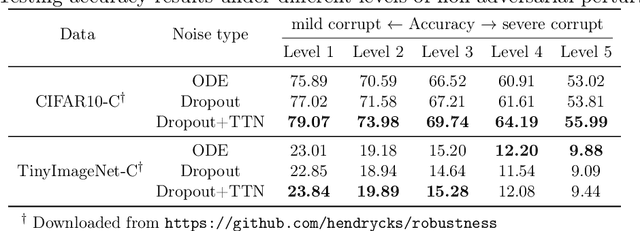
Abstract:Neural Ordinary Differential Equation (Neural ODE) has been proposed as a continuous approximation to the ResNet architecture. Some commonly used regularization mechanisms in discrete neural networks (e.g. dropout, Gaussian noise) are missing in current Neural ODE networks. In this paper, we propose a new continuous neural network framework called Neural Stochastic Differential Equation (Neural SDE) network, which naturally incorporates various commonly used regularization mechanisms based on random noise injection. Our framework can model various types of noise injection frequently used in discrete networks for regularization purpose, such as dropout and additive/multiplicative noise in each block. We provide theoretical analysis explaining the improved robustness of Neural SDE models against input perturbations/adversarial attacks. Furthermore, we demonstrate that the Neural SDE network can achieve better generalization than the Neural ODE and is more resistant to adversarial and non-adversarial input perturbations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge