Understanding Transfer Learning via Mean-field Analysis

We propose a novel framework for exploring generalization errors of transfer learning through the lens of differential calculus on the space of probability measures. In particular, we consider two main transfer learning scenarios, $\alpha$-ERM and fine-tuning with the KL-regularized empirical risk minimization and establish generic conditions under which the generalization error and the population risk convergence rates for these scenarios are studied. Based on our theoretical results, we show the benefits of transfer learning with a one-hidden-layer neural network in the mean-field regime under some suitable integrability and regularity assumptions on the loss and activation functions.

Generalization Error of the Tilted Empirical Risk

The generalization error (risk) of a supervised statistical learning algorithm quantifies its prediction ability on previously unseen data. Inspired by exponential tilting, Li et al. (2021) proposed the tilted empirical risk as a non-linear risk metric for machine learning applications such as classification and regression problems. In this work, we examine the generalization error of the tilted empirical risk. In particular, we provide uniform and information-theoretic bounds on the tilted generalization error, defined as the difference between the population risk and the tilted empirical risk, with a convergence rate of $O(1/\sqrt{n})$ where $n$ is the number of training samples. Furthermore, we study the solution to the KL-regularized expected tilted empirical risk minimization problem and derive an upper bound on the expected tilted generalization error with a convergence rate of $O(1/n)$.

Generalization Error of Graph Neural Networks in the Mean-field Regime

This work provides a theoretical framework for assessing the generalization error of graph classification tasks via graph neural networks in the over-parameterized regime, where the number of parameters surpasses the quantity of data points. We explore two widely utilized types of graph neural networks: graph convolutional neural networks and message passing graph neural networks. Prior to this study, existing bounds on the generalization error in the over-parametrized regime were uninformative, limiting our understanding of over-parameterized network performance. Our novel approach involves deriving upper bounds within the mean-field regime for evaluating the generalization error of these graph neural networks. We establish upper bounds with a convergence rate of $O(1/n)$, where $n$ is the number of graph samples. These upper bounds offer a theoretical assurance of the networks' performance on unseen data in the challenging over-parameterized regime and overall contribute to our understanding of their performance.

Mean-field Analysis of Generalization Errors

We propose a novel framework for exploring weak and $L_2$ generalization errors of algorithms through the lens of differential calculus on the space of probability measures. Specifically, we consider the KL-regularized empirical risk minimization problem and establish generic conditions under which the generalization error convergence rate, when training on a sample of size $n$, is $\mathcal{O}(1/n)$. In the context of supervised learning with a one-hidden layer neural network in the mean-field regime, these conditions are reflected in suitable integrability and regularity assumptions on the loss and activation functions.

Global Convergence of Deep Galerkin and PINNs Methods for Solving Partial Differential Equations

Numerically solving high-dimensional partial differential equations (PDEs) is a major challenge. Conventional methods, such as finite difference methods, are unable to solve high-dimensional PDEs due to the curse-of-dimensionality. A variety of deep learning methods have been recently developed to try and solve high-dimensional PDEs by approximating the solution using a neural network. In this paper, we prove global convergence for one of the commonly-used deep learning algorithms for solving PDEs, the Deep Galerkin Method (DGM). DGM trains a neural network approximator to solve the PDE using stochastic gradient descent. We prove that, as the number of hidden units in the single-layer network goes to infinity (i.e., in the ``wide network limit"), the trained neural network converges to the solution of an infinite-dimensional linear ordinary differential equation (ODE). The PDE residual of the limiting approximator converges to zero as the training time $\rightarrow \infty$. Under mild assumptions, this convergence also implies that the neural network approximator converges to the solution of the PDE. A closely related class of deep learning methods for PDEs is Physics Informed Neural Networks (PINNs). Using the same mathematical techniques, we can prove a similar global convergence result for the PINN neural network approximators. Both proofs require analyzing a kernel function in the limit ODE governing the evolution of the limit neural network approximator. A key technical challenge is that the kernel function, which is a composition of the PDE operator and the neural tangent kernel (NTK) operator, lacks a spectral gap, therefore requiring a careful analysis of its properties.

TAPAS: a Toolbox for Adversarial Privacy Auditing of Synthetic Data

Personal data collected at scale promises to improve decision-making and accelerate innovation. However, sharing and using such data raises serious privacy concerns. A promising solution is to produce synthetic data, artificial records to share instead of real data. Since synthetic records are not linked to real persons, this intuitively prevents classical re-identification attacks. However, this is insufficient to protect privacy. We here present TAPAS, a toolbox of attacks to evaluate synthetic data privacy under a wide range of scenarios. These attacks include generalizations of prior works and novel attacks. We also introduce a general framework for reasoning about privacy threats to synthetic data and showcase TAPAS on several examples.

Hedging option books using neural-SDE market models

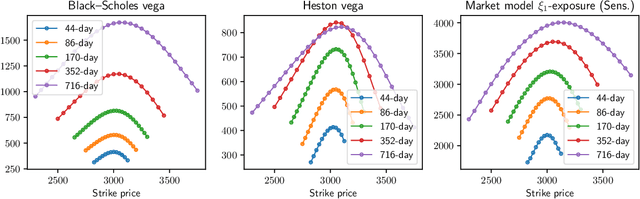
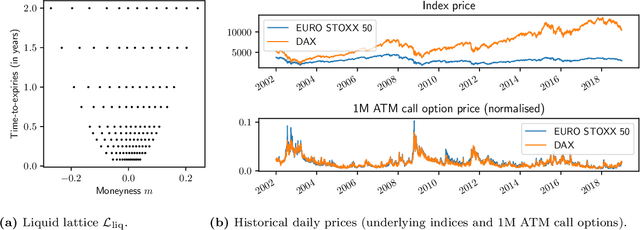
We study the capability of arbitrage-free neural-SDE market models to yield effective strategies for hedging options. In particular, we derive sensitivity-based and minimum-variance-based hedging strategies using these models and examine their performance when applied to various option portfolios using real-world data. Through backtesting analysis over typical and stressed market periods, we show that neural-SDE market models achieve lower hedging errors than Black--Scholes delta and delta-vega hedging consistently over time, and are less sensitive to the tenor choice of hedging instruments. In addition, hedging using market models leads to similar performance to hedging using Heston models, while the former tends to be more robust during stressed market periods.

Synthetic Data -- what, why and how?

This explainer document aims to provide an overview of the current state of the rapidly expanding work on synthetic data technologies, with a particular focus on privacy. The article is intended for a non-technical audience, though some formal definitions have been given to provide clarity to specialists. This article is intended to enable the reader to quickly become familiar with the notion of synthetic data, as well as understand some of the subtle intricacies that come with it. We do believe that synthetic data is a very useful tool, and our hope is that this report highlights that, while drawing attention to nuances that can easily be overlooked in its deployment.

Neural Q-learning for solving elliptic PDEs

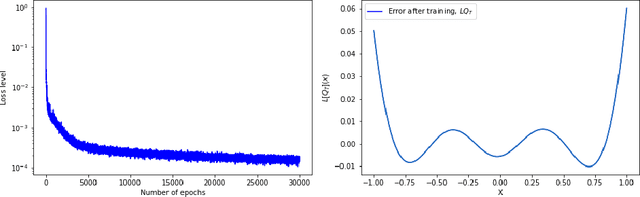
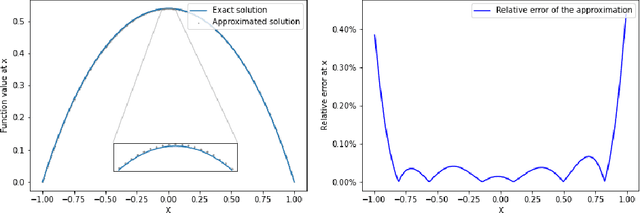
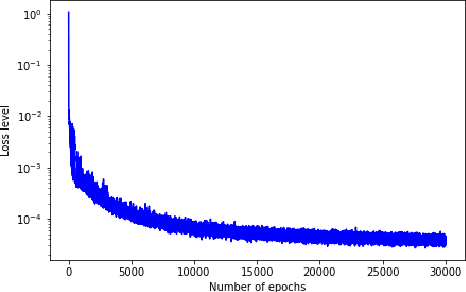
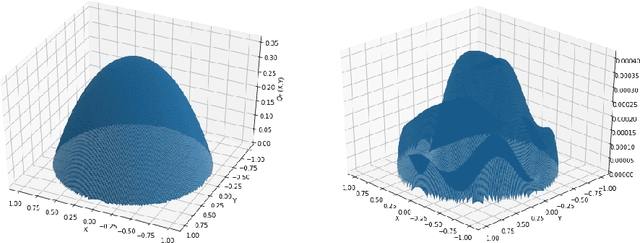
Solving high-dimensional partial differential equations (PDEs) is a major challenge in scientific computing. We develop a new numerical method for solving elliptic-type PDEs by adapting the Q-learning algorithm in reinforcement learning. Our "Q-PDE" algorithm is mesh-free and therefore has the potential to overcome the curse of dimensionality. Using a neural tangent kernel (NTK) approach, we prove that the neural network approximator for the PDE solution, trained with the Q-PDE algorithm, converges to the trajectory of an infinite-dimensional ordinary differential equation (ODE) as the number of hidden units $\rightarrow \infty$. For monotone PDE (i.e. those given by monotone operators, which may be nonlinear), despite the lack of a spectral gap in the NTK, we then prove that the limit neural network, which satisfies the infinite-dimensional ODE, converges in $L^2$ to the PDE solution as the training time $\rightarrow \infty$. More generally, we can prove that any fixed point of the wide-network limit for the Q-PDE algorithm is a solution of the PDE (not necessarily under the monotone condition). The numerical performance of the Q-PDE algorithm is studied for several elliptic PDEs.

Estimating risks of option books using neural-SDE market models

In this paper, we examine the capacity of an arbitrage-free neural-SDE market model to produce realistic scenarios for the joint dynamics of multiple European options on a single underlying. We subsequently demonstrate its use as a risk simulation engine for option portfolios. Through backtesting analysis, we show that our models are more computationally efficient and accurate for evaluating the Value-at-Risk (VaR) of option portfolios, with better coverage performance and less procyclicality than standard filtered historical simulation approaches.