Neural Actor-Critic Methods for Hamilton-Jacobi-Bellman PDEs: Asymptotic Analysis and Numerical Studies

We mathematically analyze and numerically study an actor-critic machine learning algorithm for solving high-dimensional Hamilton-Jacobi-Bellman (HJB) partial differential equations from stochastic control theory. The architecture of the critic (the estimator for the value function) is structured so that the boundary condition is always perfectly satisfied (rather than being included in the training loss) and utilizes a biased gradient which reduces computational cost. The actor (the estimator for the optimal control) is trained by minimizing the integral of the Hamiltonian over the domain, where the Hamiltonian is estimated using the critic. We show that the training dynamics of the actor and critic neural networks converge in a Sobolev-type space to a certain infinite-dimensional ordinary differential equation (ODE) as the number of hidden units in the actor and critic $\rightarrow \infty$. Further, under a convexity-like assumption on the Hamiltonian, we prove that any fixed point of this limit ODE is a solution of the original stochastic control problem. This provides an important guarantee for the algorithm's performance in light of the fact that finite-width neural networks may only converge to a local minimizers (and not optimal solutions) due to the non-convexity of their loss functions. In our numerical studies, we demonstrate that the algorithm can solve stochastic control problems accurately in up to 200 dimensions. In particular, we construct a series of increasingly complex stochastic control problems with known analytic solutions and study the algorithm's numerical performance on them. These problems range from a linear-quadratic regulator equation to highly challenging equations with non-convex Hamiltonians, allowing us to identify and analyze the strengths and limitations of this neural actor-critic method for solving HJB equations.

Global Convergence of Deep Galerkin and PINNs Methods for Solving Partial Differential Equations

Numerically solving high-dimensional partial differential equations (PDEs) is a major challenge. Conventional methods, such as finite difference methods, are unable to solve high-dimensional PDEs due to the curse-of-dimensionality. A variety of deep learning methods have been recently developed to try and solve high-dimensional PDEs by approximating the solution using a neural network. In this paper, we prove global convergence for one of the commonly-used deep learning algorithms for solving PDEs, the Deep Galerkin Method (DGM). DGM trains a neural network approximator to solve the PDE using stochastic gradient descent. We prove that, as the number of hidden units in the single-layer network goes to infinity (i.e., in the ``wide network limit"), the trained neural network converges to the solution of an infinite-dimensional linear ordinary differential equation (ODE). The PDE residual of the limiting approximator converges to zero as the training time $\rightarrow \infty$. Under mild assumptions, this convergence also implies that the neural network approximator converges to the solution of the PDE. A closely related class of deep learning methods for PDEs is Physics Informed Neural Networks (PINNs). Using the same mathematical techniques, we can prove a similar global convergence result for the PINN neural network approximators. Both proofs require analyzing a kernel function in the limit ODE governing the evolution of the limit neural network approximator. A key technical challenge is that the kernel function, which is a composition of the PDE operator and the neural tangent kernel (NTK) operator, lacks a spectral gap, therefore requiring a careful analysis of its properties.

Neural Q-learning for solving elliptic PDEs

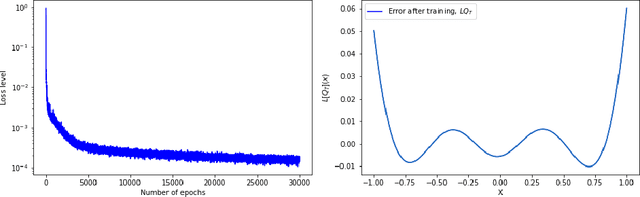
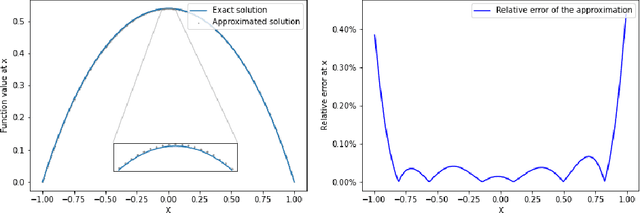
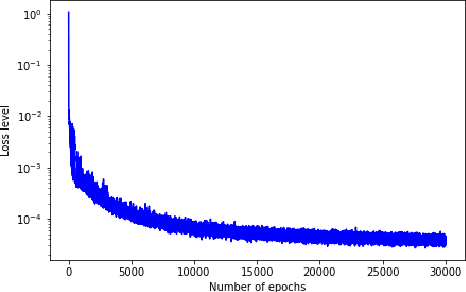
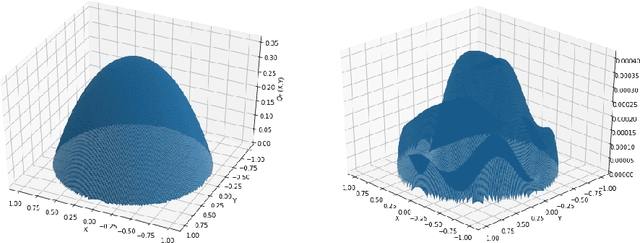
Solving high-dimensional partial differential equations (PDEs) is a major challenge in scientific computing. We develop a new numerical method for solving elliptic-type PDEs by adapting the Q-learning algorithm in reinforcement learning. Our "Q-PDE" algorithm is mesh-free and therefore has the potential to overcome the curse of dimensionality. Using a neural tangent kernel (NTK) approach, we prove that the neural network approximator for the PDE solution, trained with the Q-PDE algorithm, converges to the trajectory of an infinite-dimensional ordinary differential equation (ODE) as the number of hidden units $\rightarrow \infty$. For monotone PDE (i.e. those given by monotone operators, which may be nonlinear), despite the lack of a spectral gap in the NTK, we then prove that the limit neural network, which satisfies the infinite-dimensional ODE, converges in $L^2$ to the PDE solution as the training time $\rightarrow \infty$. More generally, we can prove that any fixed point of the wide-network limit for the Q-PDE algorithm is a solution of the PDE (not necessarily under the monotone condition). The numerical performance of the Q-PDE algorithm is studied for several elliptic PDEs.