Logit Attenuating Weight Normalization

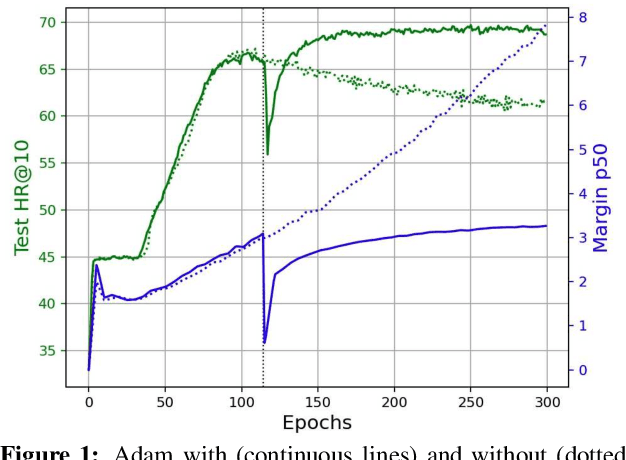
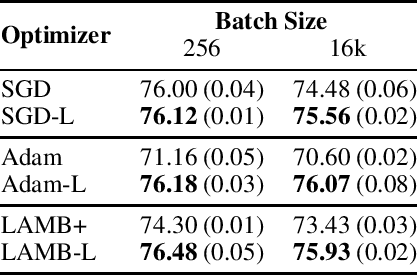
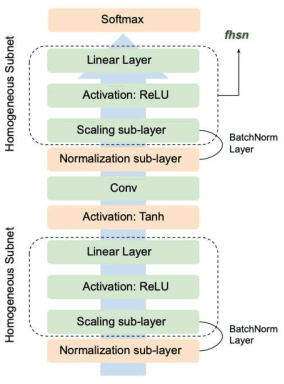
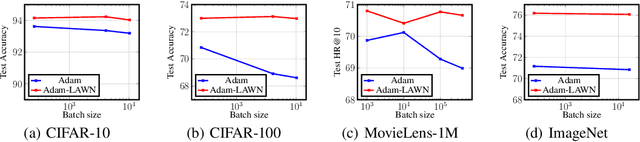
Over-parameterized deep networks trained using gradient-based optimizers are a popular choice for solving classification and ranking problems. Without appropriately tuned $\ell_2$ regularization or weight decay, such networks have the tendency to make output scores (logits) and network weights large, causing training loss to become too small and the network to lose its adaptivity (ability to move around) in the parameter space. Although regularization is typically understood from an overfitting perspective, we highlight its role in making the network more adaptive and enabling it to escape more easily from weights that generalize poorly. To provide such a capability, we propose a method called Logit Attenuating Weight Normalization (LAWN), that can be stacked onto any gradient-based optimizer. LAWN controls the logits by constraining the weight norms of layers in the final homogeneous sub-network. Empirically, we show that the resulting LAWN variant of the optimizer makes a deep network more adaptive to finding minimas with superior generalization performance on large-scale image classification and recommender systems. While LAWN is particularly impressive in improving Adam, it greatly improves all optimizers when used with large batch sizes

Regression via Implicit Models and Optimal Transport Cost Minimization

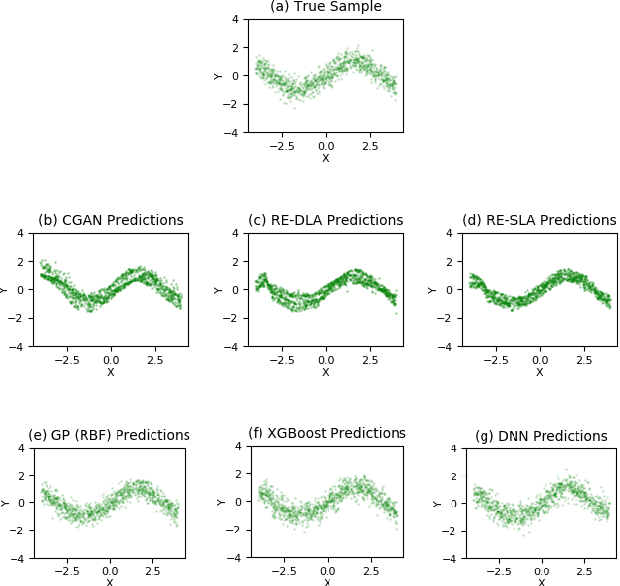
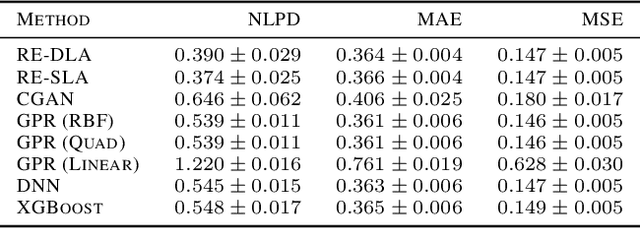
This paper addresses the classic problem of regression, which involves the inductive learning of a map, $y=f(x,z)$, $z$ denoting noise, $f:\mathbb{R}^n\times \mathbb{R}^k \rightarrow \mathbb{R}^m$. Recently, Conditional GAN (CGAN) has been applied for regression and has shown to be advantageous over the other standard approaches like Gaussian Process Regression, given its ability to implicitly model complex noise forms. However, the current CGAN implementation for regression uses the classical generator-discriminator architecture with the minimax optimization approach, which is notorious for being difficult to train due to issues like training instability or failure to converge. In this paper, we take another step towards regression models that implicitly model the noise, and propose a solution which directly optimizes the optimal transport cost between the true probability distribution $p(y|x)$ and the estimated distribution $\hat{p}(y|x)$ and does not suffer from the issues associated with the minimax approach. On a variety of synthetic and real-world datasets, our proposed solution achieves state-of-the-art results. The code accompanying this paper is available at "https://github.com/gurdaspuriya/ot_regression".

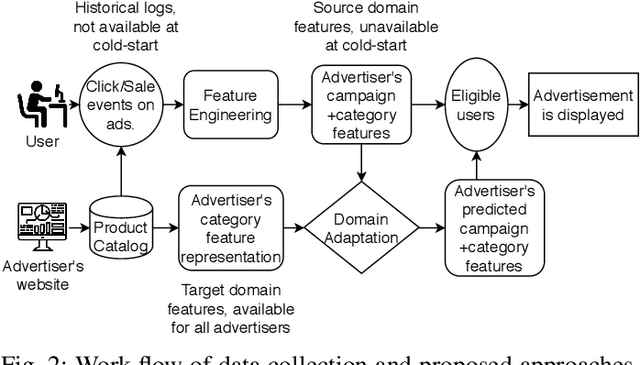
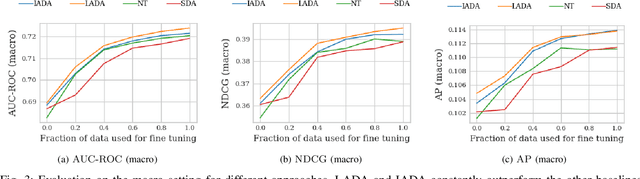
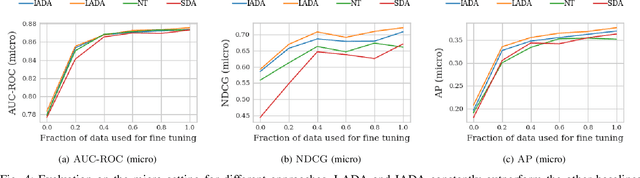
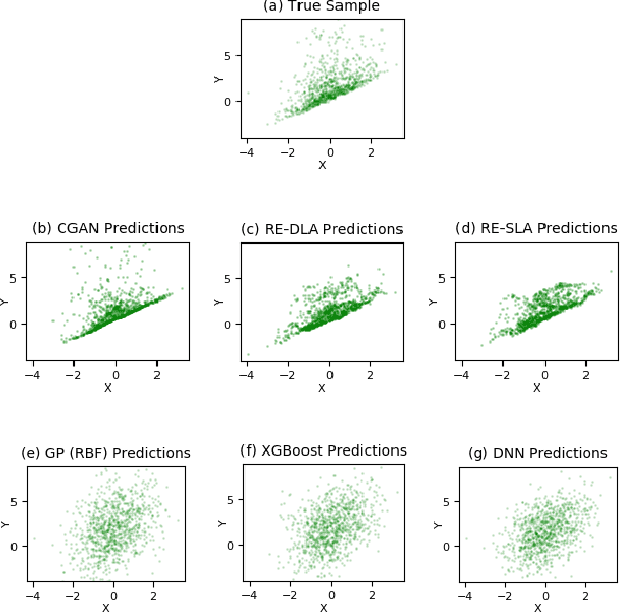
Targeted display advertising: the case of preferential attachment

An average adult is exposed to hundreds of digital advertisements daily (https://www.mediadynamicsinc.com/uploads/files/PR092214-Note-only-150-Ads-2mk.pdf), making the digital advertisement industry a classic example of a big-data-driven platform. As such, the ad-tech industry relies on historical engagement logs (clicks or purchases) to identify potentially interested users for the advertisement campaign of a partner (a seller who wants to target users for its products). The number of advertisements that are shown for a partner, and hence the historical campaign data available for a partner depends upon the budget constraints of the partner. Thus, enough data can be collected for the high-budget partners to make accurate predictions, while this is not the case with the low-budget partners. This skewed distribution of the data leads to "preferential attachment" of the targeted display advertising platforms towards the high-budget partners. In this paper, we develop "domain-adaptation" approaches to address the challenge of predicting interested users for the partners with insufficient data, i.e., the tail partners. Specifically, we develop simple yet effective approaches that leverage the similarity among the partners to transfer information from the partners with sufficient data to cold-start partners, i.e., partners without any campaign data. Our approaches readily adapt to the new campaign data by incremental fine-tuning, and hence work at varying points of a campaign, and not just the cold-start. We present an experimental analysis on the historical logs of a major display advertising platform (https://www.criteo.com/). Specifically, we evaluate our approaches across 149 partners, at varying points of their campaigns. Experimental results show that the proposed approaches outperform the other "domain-adaptation" approaches at different time points of the campaigns.

Regression with Conditional GAN

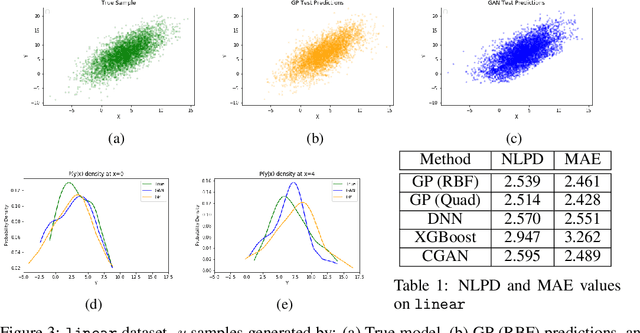
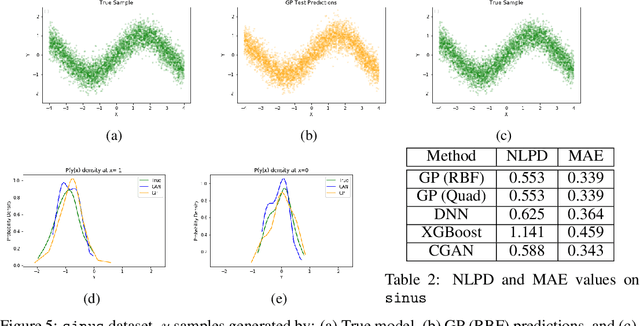
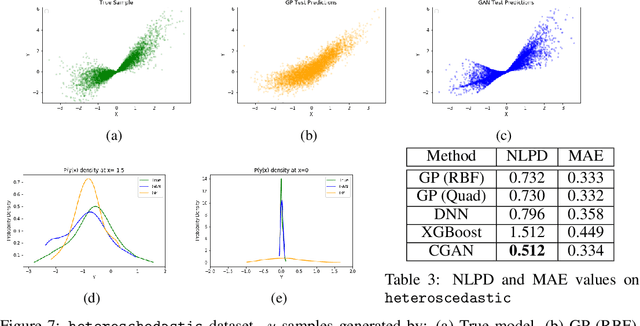
In recent years, impressive progress has been made in the design of implicit probabilistic models via Generative Adversarial Networks (GAN) and its extension, the Conditional GAN (CGAN). Excellent solutions have been demonstrated mostly in image processing applications which involve large, continuous output spaces. There is almost no application of these powerful tools to problems having small dimensional output spaces. Regression problems involving the inductive learning of a map, $y=f(x,z)$, $z$ denoting noise, $f:\mathbb{R}^n\times \mathbb{R}^k \rightarrow \mathbb{R}^m$, with $m$ small (e.g., $m=1$ or just a few) is one good case in point. The standard approach to solve regression problems is to probabilistically model the output $y$ as the sum of a mean function $m(x)$ and a noise term $z$; it is also usual to take the noise to be a Gaussian. These are done for convenience sake so that the likelihood of observed data is expressible in closed form. In the real world, on the other hand, stochasticity of the output is usually caused by missing or noisy input variables. Such a real world situation is best represented using an implicit model in which an extra noise vector, $z$ is included with $x$ as input. CGAN is naturally suited to design such implicit models. This paper makes the first step in this direction. Through several artificial and real world datasets, we demonstrate CGAN to be an effective approach for solving regression problems. We compare against Gaussian Processes and show that CGAN has excellent output likelihood properties and possesses the ability to model complex noise forms in a better way.

Learning State Representations for Query Optimization with Deep Reinforcement Learning

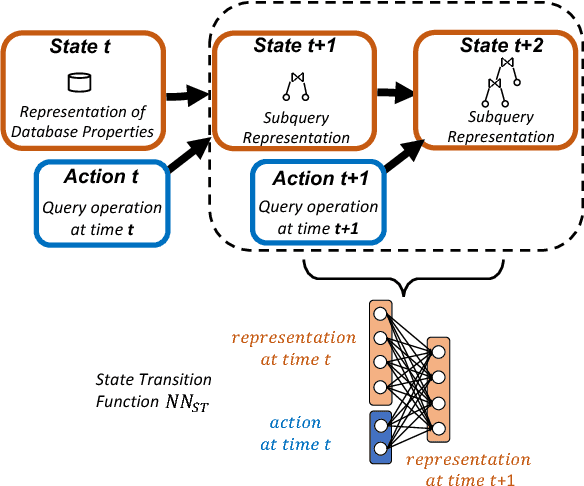
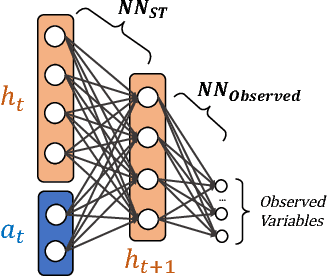
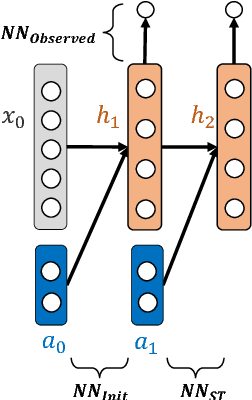
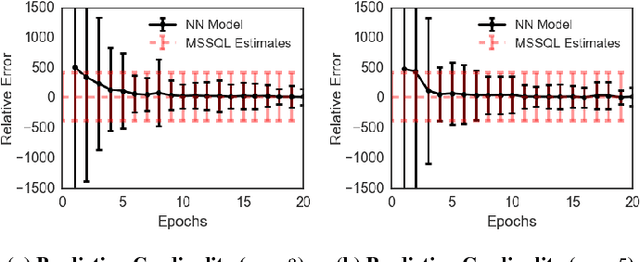
Deep reinforcement learning is quickly changing the field of artificial intelligence. These models are able to capture a high level understanding of their environment, enabling them to learn difficult dynamic tasks in a variety of domains. In the database field, query optimization remains a difficult problem. Our goal in this work is to explore the capabilities of deep reinforcement learning in the context of query optimization. At each state, we build queries incrementally and encode properties of subqueries through a learned representation. The challenge here lies in the formation of the state transition function, which defines how the current subquery state combines with the next query operation (action) to yield the next state. As a first step in this direction, we focus the state representation problem and the formation of the state transition function. We describe our approach and show preliminary results. We further discuss how we can use the state representation to improve query optimization using reinforcement learning.

Batch-Expansion Training: An Efficient Optimization Framework

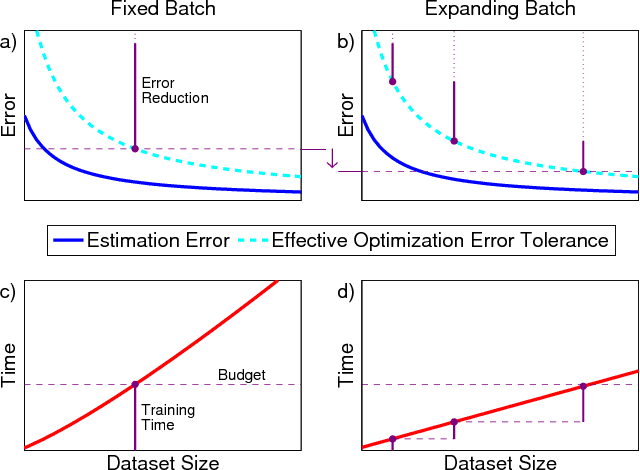
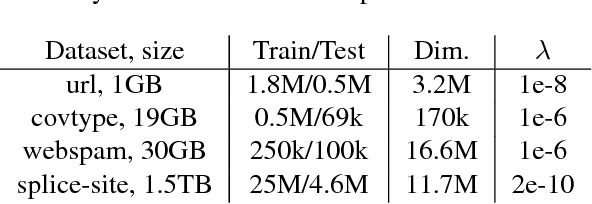
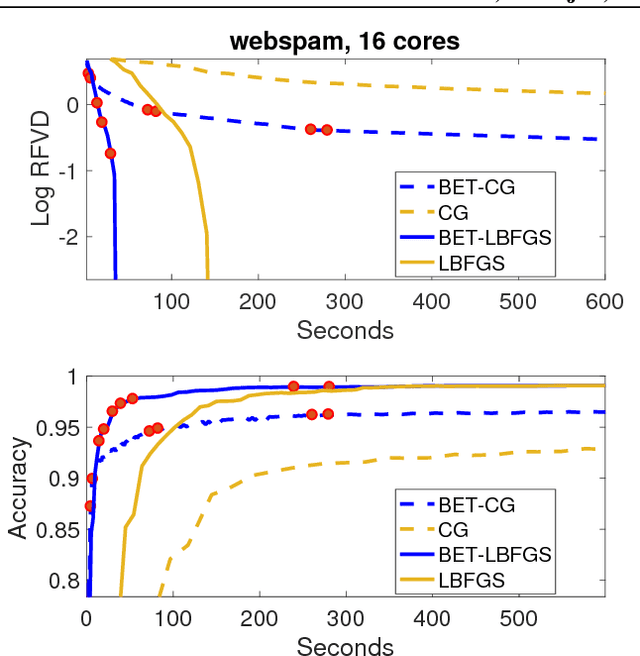
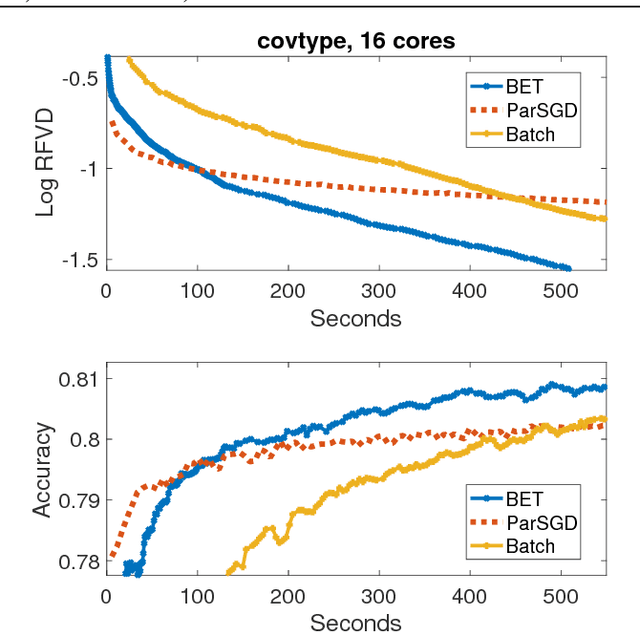
We propose Batch-Expansion Training (BET), a framework for running a batch optimizer on a gradually expanding dataset. As opposed to stochastic approaches, batches do not need to be resampled i.i.d. at every iteration, thus making BET more resource efficient in a distributed setting, and when disk-access is constrained. Moreover, BET can be easily paired with most batch optimizers, does not require any parameter-tuning, and compares favorably to existing stochastic and batch methods. We show that when the batch size grows exponentially with the number of outer iterations, BET achieves optimal $O(1/\epsilon)$ data-access convergence rate for strongly convex objectives. Experiments in parallel and distributed settings show that BET performs better than standard batch and stochastic approaches.

Distributed Newton Methods for Deep Neural Networks

Deep learning involves a difficult non-convex optimization problem with a large number of weights between any two adjacent layers of a deep structure. To handle large data sets or complicated networks, distributed training is needed, but the calculation of function, gradient, and Hessian is expensive. In particular, the communication and the synchronization cost may become a bottleneck. In this paper, we focus on situations where the model is distributedly stored, and propose a novel distributed Newton method for training deep neural networks. By variable and feature-wise data partitions, and some careful designs, we are able to explicitly use the Jacobian matrix for matrix-vector products in the Newton method. Some techniques are incorporated to reduce the running time as well as the memory consumption. First, to reduce the communication cost, we propose a diagonalization method such that an approximate Newton direction can be obtained without communication between machines. Second, we consider subsampled Gauss-Newton matrices for reducing the running time as well as the communication cost. Third, to reduce the synchronization cost, we terminate the process of finding an approximate Newton direction even though some nodes have not finished their tasks. Details of some implementation issues in distributed environments are thoroughly investigated. Experiments demonstrate that the proposed method is effective for the distributed training of deep neural networks. In compared with stochastic gradient methods, it is more robust and may give better test accuracy.

Towards a Better Understanding of Predict and Count Models

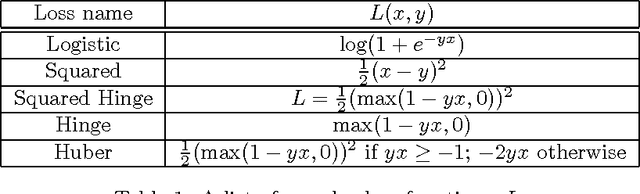
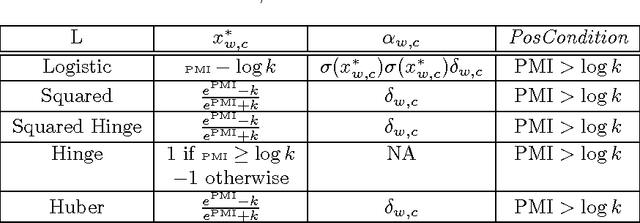
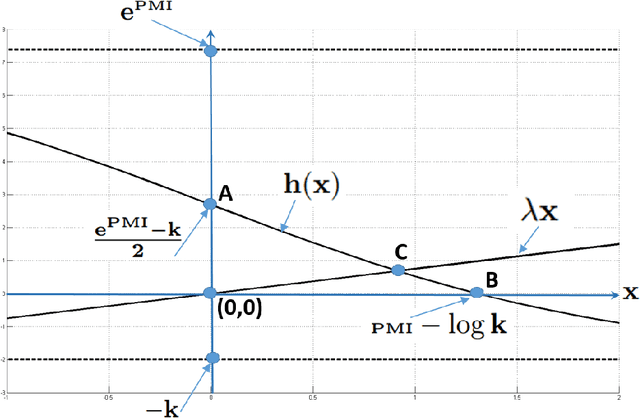
In a recent paper, Levy and Goldberg pointed out an interesting connection between prediction-based word embedding models and count models based on pointwise mutual information. Under certain conditions, they showed that both models end up optimizing equivalent objective functions. This paper explores this connection in more detail and lays out the factors leading to differences between these models. We find that the most relevant differences from an optimization perspective are (i) predict models work in a low dimensional space where embedding vectors can interact heavily; (ii) since predict models have fewer parameters, they are less prone to overfitting. Motivated by the insight of our analysis, we show how count models can be regularized in a principled manner and provide closed-form solutions for L1 and L2 regularization. Finally, we propose a new embedding model with a convex objective and the additional benefit of being intelligible.

A distributed block coordinate descent method for training $l_1$ regularized linear classifiers

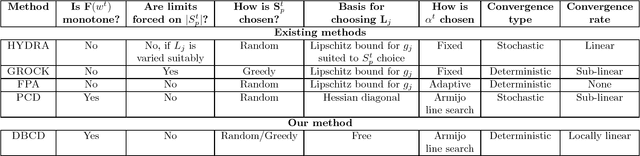
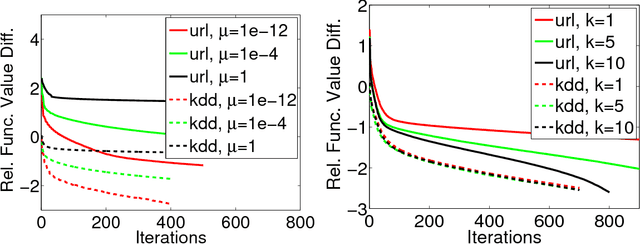
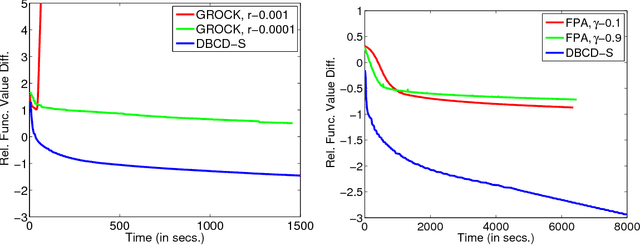
Distributed training of $l_1$ regularized classifiers has received great attention recently. Most existing methods approach this problem by taking steps obtained from approximating the objective by a quadratic approximation that is decoupled at the individual variable level. These methods are designed for multicore and MPI platforms where communication costs are low. They are inefficient on systems such as Hadoop running on a cluster of commodity machines where communication costs are substantial. In this paper we design a distributed algorithm for $l_1$ regularization that is much better suited for such systems than existing algorithms. A careful cost analysis is used to support these points and motivate our method. The main idea of our algorithm is to do block optimization of many variables on the actual objective function within each computing node; this increases the computational cost per step that is matched with the communication cost, and decreases the number of outer iterations, thus yielding a faster overall method. Distributed Gauss-Seidel and Gauss-Southwell greedy schemes are used for choosing variables to update in each step. We establish global convergence theory for our algorithm, including Q-linear rate of convergence. Experiments on two benchmark problems show our method to be much faster than existing methods.

An efficient distributed learning algorithm based on effective local functional approximations

Scalable machine learning over big data is an important problem that is receiving a lot of attention in recent years. On popular distributed environments such as Hadoop running on a cluster of commodity machines, communication costs are substantial and algorithms need to be designed suitably considering those costs. In this paper we give a novel approach to the distributed training of linear classifiers (involving smooth losses and L2 regularization) that is designed to reduce the total communication costs. At each iteration, the nodes minimize locally formed approximate objective functions; then the resulting minimizers are combined to form a descent direction to move. Our approach gives a lot of freedom in the formation of the approximate objective function as well as in the choice of methods to solve them. The method is shown to have $O(log(1/\epsilon))$ time convergence. The method can be viewed as an iterative parameter mixing method. A special instantiation yields a parallel stochastic gradient descent method with strong convergence. When communication times between nodes are large, our method is much faster than the Terascale method (Agarwal et al., 2011), which is a state of the art distributed solver based on the statistical query model (Chuet al., 2006) that computes function and gradient values in a distributed fashion. We also evaluate against other recent distributed methods and demonstrate superior performance of our method.