Gen-AI for User Safety: A Survey

Machine Learning and data mining techniques (i.e. supervised and unsupervised techniques) are used across domains to detect user safety violations. Examples include classifiers used to detect whether an email is spam or a web-page is requesting bank login information. However, existing ML/DM classifiers are limited in their ability to understand natural languages w.r.t the context and nuances. The aforementioned challenges are overcome with the arrival of Gen-AI techniques, along with their inherent ability w.r.t translation between languages, fine-tuning between various tasks and domains. In this manuscript, we provide a comprehensive overview of the various work done while using Gen-AI techniques w.r.t user safety. In particular, we first provide the various domains (e.g. phishing, malware, content moderation, counterfeit, physical safety) across which Gen-AI techniques have been applied. Next, we provide how Gen-AI techniques can be used in conjunction with various data modalities i.e. text, images, videos, audio, executable binaries to detect violations of user-safety. Further, also provide an overview of how Gen-AI techniques can be used in an adversarial setting. We believe that this work represents the first summarization of Gen-AI techniques for user-safety.

Opportunities and Challenges of Generative-AI in Finance

Machine Learning and data mining have created widespread impact across various domains. However, these techniques are limited in their ability to reason, understand and generalize w.r.t language specific tasks. The aforementioned challenges were overcome, with the advancement of LLMs/Gen-AI. Gen-AI techniques are able to improve understanding of context and nuances in language modeling, translation between languages, handle large volumes of data, provide fast, low-latency responses and can be fine-tuned for various tasks and domains. In this manuscript, we present a comprehensive overview of the applications of Gen-AI techniques in the finance domain. In particular, we present the opportunities and challenges associated with the usage of Gen-AI techniques in finance. We also illustrate the various methodologies which can be used to train Gen-AI and present the various application areas of Gen-AI techniques in the finance ecosystem. To the best of our knowledge, this work represents the most comprehensive summarization of Gen-AI techniques within the financial domain. The analysis is designed for a deep overview of areas marked for substantial advancement while simultaneously pin-point those warranting future prioritization. We also hope that this work would serve as a conduit between finance and other domains, thus fostering the cross-pollination of innovative concepts and practices.

Regression via Implicit Models and Optimal Transport Cost Minimization

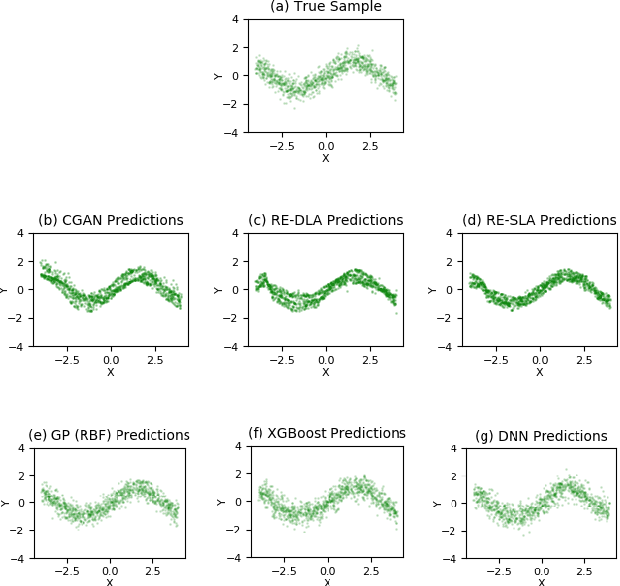
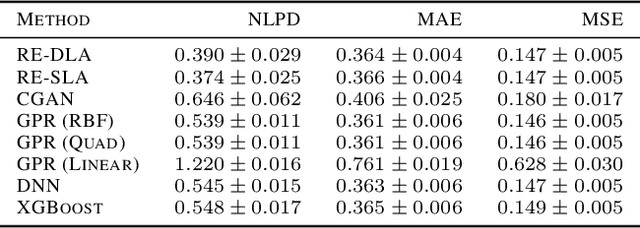
This paper addresses the classic problem of regression, which involves the inductive learning of a map, $y=f(x,z)$, $z$ denoting noise, $f:\mathbb{R}^n\times \mathbb{R}^k \rightarrow \mathbb{R}^m$. Recently, Conditional GAN (CGAN) has been applied for regression and has shown to be advantageous over the other standard approaches like Gaussian Process Regression, given its ability to implicitly model complex noise forms. However, the current CGAN implementation for regression uses the classical generator-discriminator architecture with the minimax optimization approach, which is notorious for being difficult to train due to issues like training instability or failure to converge. In this paper, we take another step towards regression models that implicitly model the noise, and propose a solution which directly optimizes the optimal transport cost between the true probability distribution $p(y|x)$ and the estimated distribution $\hat{p}(y|x)$ and does not suffer from the issues associated with the minimax approach. On a variety of synthetic and real-world datasets, our proposed solution achieves state-of-the-art results. The code accompanying this paper is available at "https://github.com/gurdaspuriya/ot_regression".

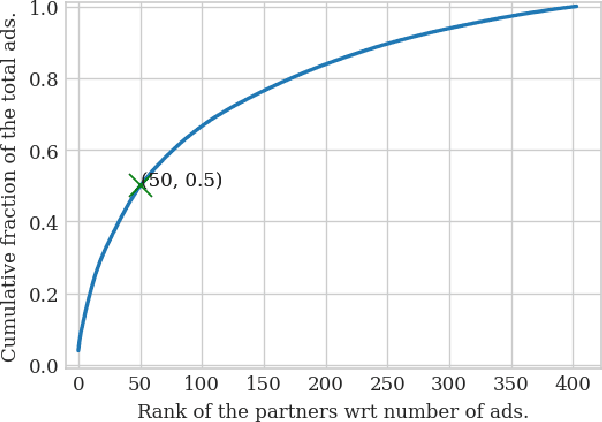
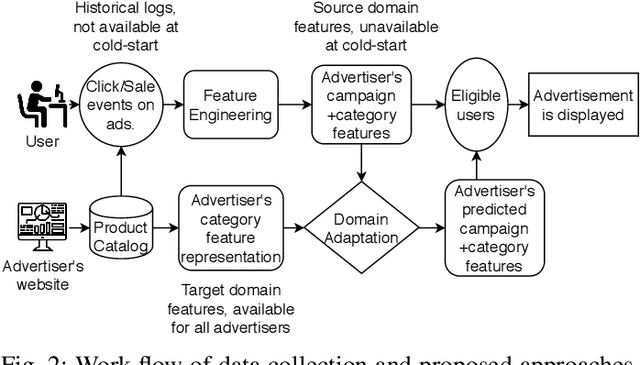
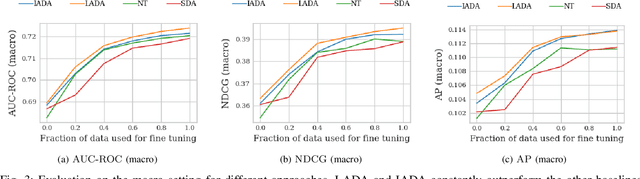
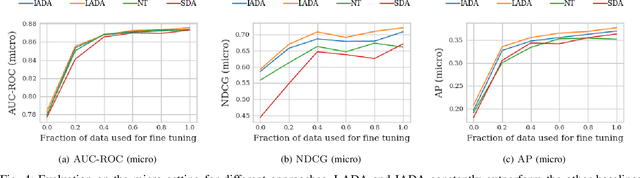
Targeted display advertising: the case of preferential attachment

An average adult is exposed to hundreds of digital advertisements daily (https://www.mediadynamicsinc.com/uploads/files/PR092214-Note-only-150-Ads-2mk.pdf), making the digital advertisement industry a classic example of a big-data-driven platform. As such, the ad-tech industry relies on historical engagement logs (clicks or purchases) to identify potentially interested users for the advertisement campaign of a partner (a seller who wants to target users for its products). The number of advertisements that are shown for a partner, and hence the historical campaign data available for a partner depends upon the budget constraints of the partner. Thus, enough data can be collected for the high-budget partners to make accurate predictions, while this is not the case with the low-budget partners. This skewed distribution of the data leads to "preferential attachment" of the targeted display advertising platforms towards the high-budget partners. In this paper, we develop "domain-adaptation" approaches to address the challenge of predicting interested users for the partners with insufficient data, i.e., the tail partners. Specifically, we develop simple yet effective approaches that leverage the similarity among the partners to transfer information from the partners with sufficient data to cold-start partners, i.e., partners without any campaign data. Our approaches readily adapt to the new campaign data by incremental fine-tuning, and hence work at varying points of a campaign, and not just the cold-start. We present an experimental analysis on the historical logs of a major display advertising platform (https://www.criteo.com/). Specifically, we evaluate our approaches across 149 partners, at varying points of their campaigns. Experimental results show that the proposed approaches outperform the other "domain-adaptation" approaches at different time points of the campaigns.

Regression with Conditional GAN

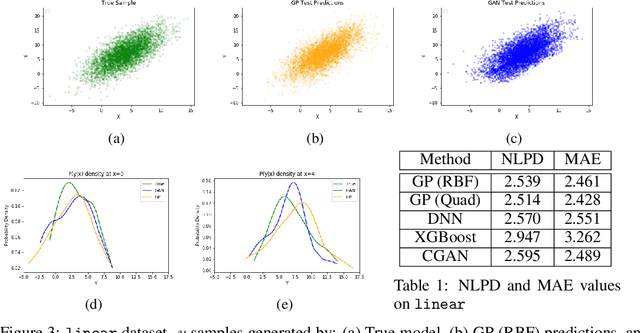
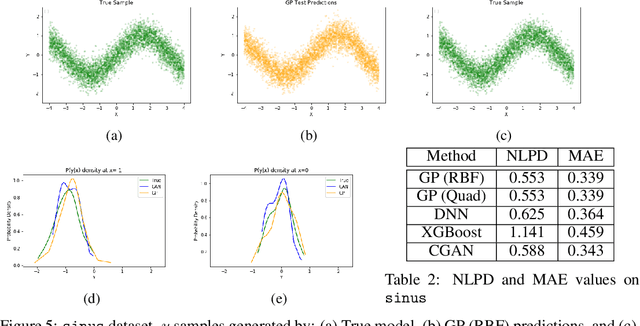
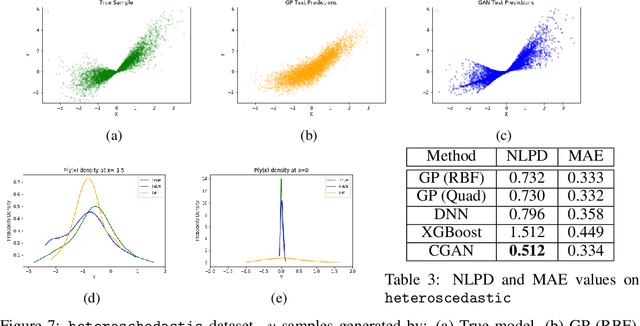
In recent years, impressive progress has been made in the design of implicit probabilistic models via Generative Adversarial Networks (GAN) and its extension, the Conditional GAN (CGAN). Excellent solutions have been demonstrated mostly in image processing applications which involve large, continuous output spaces. There is almost no application of these powerful tools to problems having small dimensional output spaces. Regression problems involving the inductive learning of a map, $y=f(x,z)$, $z$ denoting noise, $f:\mathbb{R}^n\times \mathbb{R}^k \rightarrow \mathbb{R}^m$, with $m$ small (e.g., $m=1$ or just a few) is one good case in point. The standard approach to solve regression problems is to probabilistically model the output $y$ as the sum of a mean function $m(x)$ and a noise term $z$; it is also usual to take the noise to be a Gaussian. These are done for convenience sake so that the likelihood of observed data is expressible in closed form. In the real world, on the other hand, stochasticity of the output is usually caused by missing or noisy input variables. Such a real world situation is best represented using an implicit model in which an extra noise vector, $z$ is included with $x$ as input. CGAN is naturally suited to design such implicit models. This paper makes the first step in this direction. Through several artificial and real world datasets, we demonstrate CGAN to be an effective approach for solving regression problems. We compare against Gaussian Processes and show that CGAN has excellent output likelihood properties and possesses the ability to model complex noise forms in a better way.

Reacting to Variations in Product Demand: An Application for Conversion Rate Prediction in Sponsored Search

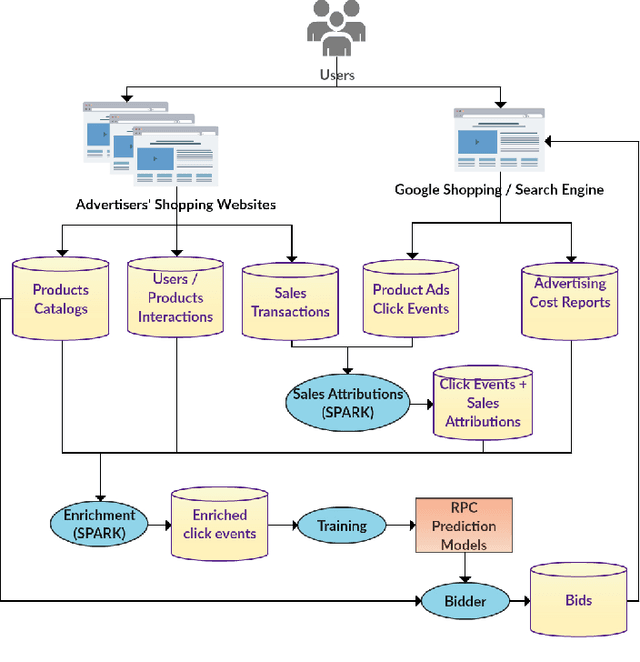
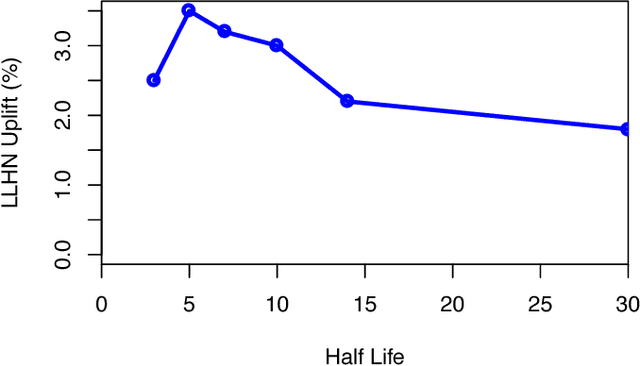
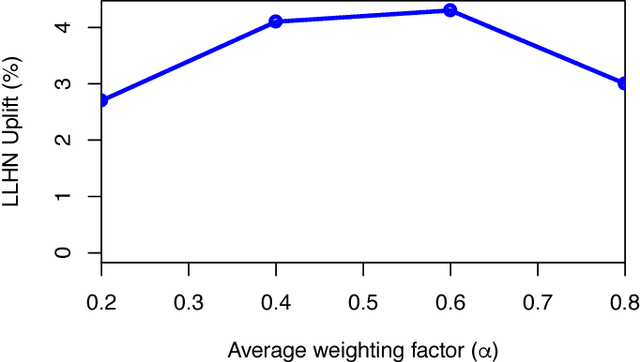
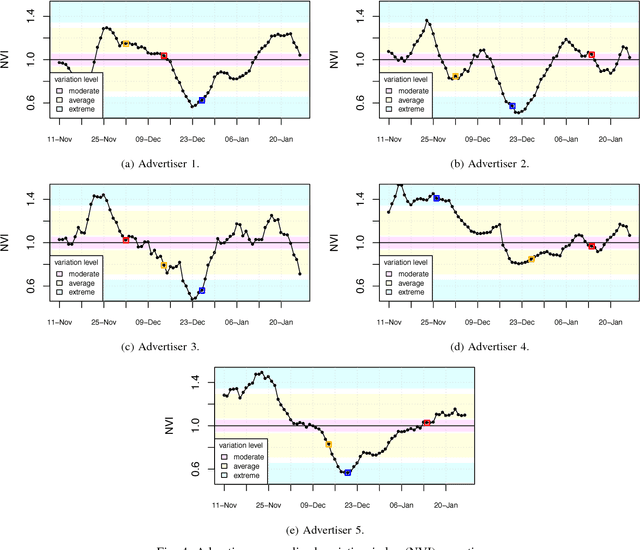
In online internet advertising, machine learning models are widely used to compute the likelihood of a user engaging with product related advertisements. However, the performance of traditional machine learning models is often impacted due to variations in user and advertiser behavior. For example, search engine traffic for florists usually tends to peak around Valentine's day, Mother's day, etc. To overcome, this challenge, in this manuscript we propose three models which are able to incorporate the effects arising due to variations in product demand. The proposed models are a combination of product demand features, specialized data sampling methodologies and ensemble techniques. We demonstrate the performance of our proposed models on datasets obtained from a real-world setting. Our results show that the proposed models more accurately predict the outcome of users interactions with product related advertisements while simultaneously being robust to fluctuations in user and advertiser behaviors.

Causal Inference in Observational Data

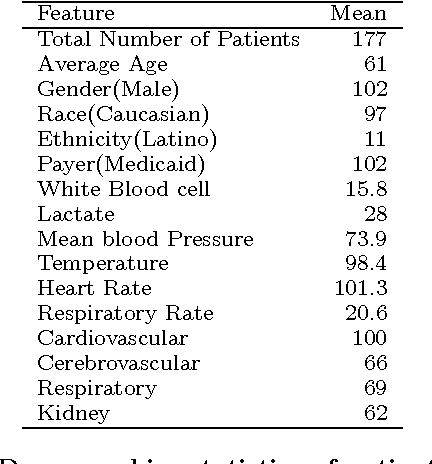
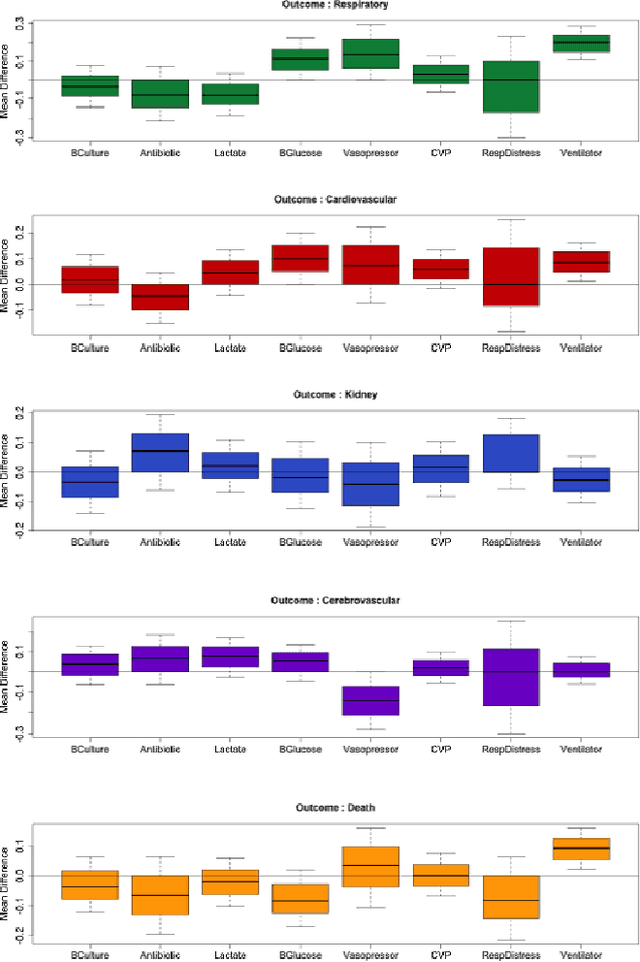
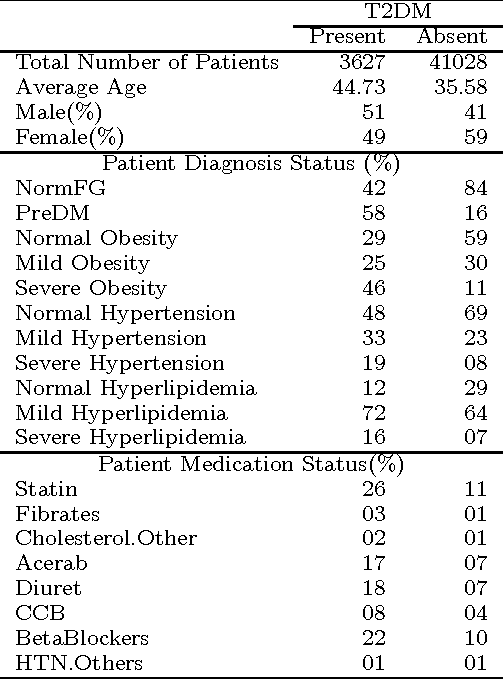
Our aging population increasingly suffers from multiple chronic diseases simultaneously, necessitating the comprehensive treatment of these conditions. Finding the optimal set of drugs for a combinatorial set of diseases is a combinatorial pattern exploration problem. Association rule mining is a popular tool for such problems, but the requirement of health care for finding causal, rather than associative, patterns renders association rule mining unsuitable. To address this issue, we propose a novel framework based on the Rubin-Neyman causal model for extracting causal rules from observational data, correcting for a number of common biases. Specifically, given a set of interventions and a set of items that define subpopulations (e.g., diseases), we wish to find all subpopulations in which effective intervention combinations exist and in each such subpopulation, we wish to find all intervention combinations such that dropping any intervention from this combination will reduce the efficacy of the treatment. A key aspect of our framework is the concept of closed intervention sets which extend the concept of quantifying the effect of a single intervention to a set of concurrent interventions. We also evaluated our causal rule mining framework on the Electronic Health Records (EHR) data of a large cohort of patients from Mayo Clinic and showed that the patterns we extracted are sufficiently rich to explain the controversial findings in the medical literature regarding the effect of a class of cholesterol drugs on Type-II Diabetes Mellitus (T2DM).