Reward Learning From Preference With Ties

Reward learning plays a pivotal role in Reinforcement Learning from Human Feedback (RLHF), ensuring the alignment of language models. The Bradley-Terry (BT) model stands as the prevalent choice for capturing human preferences from datasets containing pairs of chosen and rejected responses. In preference modeling, the focus is not on absolute values but rather on the reward difference between chosen and rejected responses, referred to as preference strength. Thus, precise evaluation of preference strength holds paramount importance in preference modeling. However, an easily overlooked factor significantly affecting preference strength measurement is that human attitudes towards two responses may not solely indicate a preference for one over the other and ties are also a common occurrence. To address this, we propose the adoption of the generalized Bradley-Terry model -- the Bradley-Terry model with ties (BTT) -- to accommodate tied preferences, thus leveraging additional information. We prove that even with the access to the true distributions of prompt and response, disregarding ties can lead to a notable bias in preference strength measurement. Comprehensive experiments further validate the advantages of incorporating ties in preference modeling. Notably, fine-tuning with BTT significantly outperforms fine-tuning with BT on synthetic preference datasets with ties, labeled by state-of-the-art open-source LLMs.

Satisficing Exploration in Bandit Optimization

Motivated by the concept of satisficing in decision-making, we consider the problem of satisficing exploration in bandit optimization. In this setting, the learner aims at selecting satisficing arms (arms with mean reward exceeding a certain threshold value) as frequently as possible. The performance is measured by satisficing regret, which is the cumulative deficit of the chosen arm's mean reward compared to the threshold. We propose SELECT, a general algorithmic template for Satisficing Exploration via LowEr Confidence bound Testing, that attains constant satisficing regret for a wide variety of bandit optimization problems in the realizable case (i.e., a satisficing arm exists). Specifically, given a class of bandit optimization problems and a corresponding learning oracle with sub-linear (standard) regret upper bound, SELECT iteratively makes use of the oracle to identify a potential satisficing arm with low regret. Then, it collects data samples from this arm, and continuously compares the LCB of the identified arm's mean reward against the threshold value to determine if it is a satisficing arm. As a complement, SELECT also enjoys the same (standard) regret guarantee as the oracle in the non-realizable case. Finally, we conduct numerical experiments to validate the performance of SELECT for several popular bandit optimization settings.

Efficient and Interpretable Bandit Algorithms

Motivated by the importance of explainability in modern machine learning, we design bandit algorithms that are \emph{efficient} and \emph{interpretable}. A bandit algorithm is interpretable if it explores with the objective of reducing uncertainty in the unknown model parameter. To quantify the interpretability, we introduce a novel metric of \textit{uncertainty loss}, which compares the rate of the uncertainty reduction to the theoretical optimum. We propose CODE, a bandit algorithm based on a \textbf{C}onstrained \textbf{O}ptimal \textbf{DE}sign, that is interpretable and maximally reduces the uncertainty. The key idea in \code is to explore among all plausible actions, determined by a statistical constraint, to achieve interpretability. We implement CODE efficiently in both multi-armed and linear bandits and derive near-optimal regret bounds by leveraging the optimality criteria of the approximate optimal design. CODE can be also viewed as removing phases in conventional phased elimination, which makes it more practical and general. We demonstrate the advantage of \code by numerical experiments on both synthetic and real-world problems. CODE outperforms other state-of-the-art interpretable designs while matching the performance of popular but uninterpretable designs, such as upper confidence bound algorithms.

User Experience Design Professionals' Perceptions of Generative Artificial Intelligence

Among creative professionals, Generative Artificial Intelligence (GenAI) has sparked excitement over its capabilities and fear over unanticipated consequences. How does GenAI impact User Experience Design (UXD) practice, and are fears warranted? We interviewed 20 UX Designers, with diverse experience and across companies (startups to large enterprises). We probed them to characterize their practices, and sample their attitudes, concerns, and expectations. We found that experienced designers are confident in their originality, creativity, and empathic skills, and find GenAI's role as assistive. They emphasized the unique human factors of "enjoyment" and "agency", where humans remain the arbiters of "AI alignment". However, skill degradation, job replacement, and creativity exhaustion can adversely impact junior designers. We discuss implications for human-GenAI collaboration, specifically copyright and ownership, human creativity and agency, and AI literacy and access. Through the lens of responsible and participatory AI, we contribute a deeper understanding of GenAI fears and opportunities for UXD.

Phase Transitions in Learning and Earning under Price Protection Guarantee

Motivated by the prevalence of ``price protection guarantee", which allows a customer who purchased a product in the past to receive a refund from the seller during the so-called price protection period (typically defined as a certain time window after the purchase date) in case the seller decides to lower the price, we study the impact of such policy on the design of online learning algorithm for data-driven dynamic pricing with initially unknown customer demand. We consider a setting where a firm sells a product over a horizon of $T$ time steps. For this setting, we characterize how the value of $M$, the length of price protection period, can affect the optimal regret of the learning process. We show that the optimal regret is $\tilde{\Theta}(\sqrt{T}+\min\{M,\,T^{2/3}\})$ by first establishing a fundamental impossible regime with novel regret lower bound instances. Then, we propose LEAP, a phased exploration type algorithm for \underline{L}earning and \underline{EA}rning under \underline{P}rice Protection to match this lower bound up to logarithmic factors or even doubly logarithmic factors (when there are only two prices available to the seller). Our results reveal the surprising phase transitions of the optimal regret with respect to $M$. Specifically, when $M$ is not too large, the optimal regret has no major difference when compared to that of the classic setting with no price protection guarantee. We also show that there exists an upper limit on how much the optimal regret can deteriorate when $M$ grows large. Finally, we conduct extensive numerical experiments to show the benefit of LEAP over other heuristic methods for this problem.

Learning to Price Supply Chain Contracts against a Learning Retailer

The rise of big data analytics has automated the decision-making of companies and increased supply chain agility. In this paper, we study the supply chain contract design problem faced by a data-driven supplier who needs to respond to the inventory decisions of the downstream retailer. Both the supplier and the retailer are uncertain about the market demand and need to learn about it sequentially. The goal for the supplier is to develop data-driven pricing policies with sublinear regret bounds under a wide range of possible retailer inventory policies for a fixed time horizon. To capture the dynamics induced by the retailer's learning policy, we first make a connection to non-stationary online learning by following the notion of variation budget. The variation budget quantifies the impact of the retailer's learning strategy on the supplier's decision-making. We then propose dynamic pricing policies for the supplier for both discrete and continuous demand. We also note that our proposed pricing policy only requires access to the support of the demand distribution, but critically, does not require the supplier to have any prior knowledge about the retailer's learning policy or the demand realizations. We examine several well-known data-driven policies for the retailer, including sample average approximation, distributionally robust optimization, and parametric approaches, and show that our pricing policies lead to sublinear regret bounds in all these cases. At the managerial level, we answer affirmatively that there is a pricing policy with a sublinear regret bound under a wide range of retailer's learning policies, even though she faces a learning retailer and an unknown demand distribution. Our work also provides a novel perspective in data-driven operations management where the principal has to learn to react to the learning policies employed by other agents in the system.

Risk-Aware Linear Bandits: Theory and Applications in Smart Order Routing

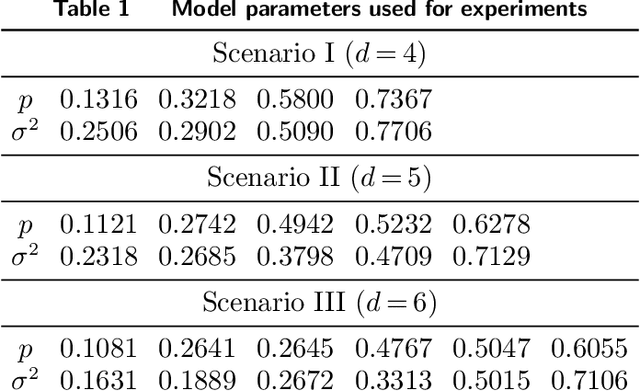
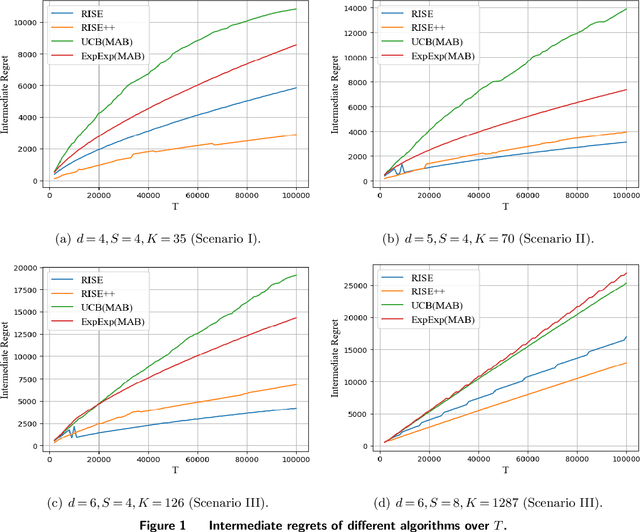
Motivated by practical considerations in machine learning for financial decision-making, such as risk-aversion and large action space, we initiate the study of risk-aware linear bandits. Specifically, we consider regret minimization under the mean-variance measure when facing a set of actions whose rewards can be expressed as linear functions of (initially) unknown parameters. Driven by the variance-minimizing G-optimal design, we propose the Risk-Aware Explore-then-Commit (RISE) algorithm and the Risk-Aware Successive Elimination (RISE++) algorithm. Then, we rigorously analyze their regret upper bounds to show that, by leveraging the linear structure, the algorithms can dramatically reduce the regret when compared to existing methods. Finally, we demonstrate the performance of the algorithms by conducting extensive numerical experiments in a synthetic smart order routing setup. Our results show that both RISE and RISE++ can outperform the competing methods, especially in complex decision-making scenarios.

Safe Optimal Design with Applications in Policy Learning

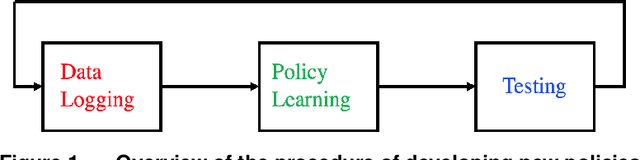
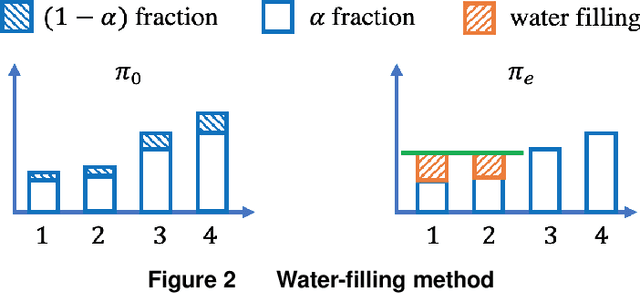
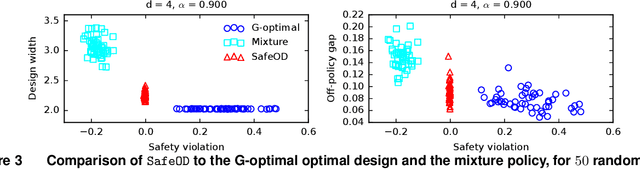
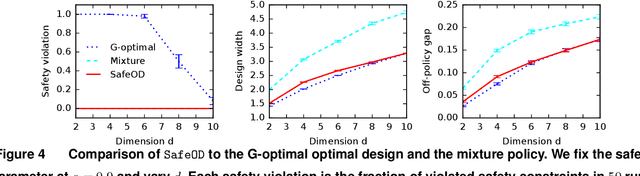
Motivated by practical needs in online experimentation and off-policy learning, we study the problem of safe optimal design, where we develop a data logging policy that efficiently explores while achieving competitive rewards with a baseline production policy. We first show, perhaps surprisingly, that a common practice of mixing the production policy with uniform exploration, despite being safe, is sub-optimal in maximizing information gain. Then we propose a safe optimal logging policy for the case when no side information about the actions' expected rewards is available. We improve upon this design by considering side information and also extend both approaches to a large number of actions with a linear reward model. We analyze how our data logging policies impact errors in off-policy learning. Finally, we empirically validate the benefit of our designs by conducting extensive experiments.

Near-Optimal Regret Bounds for Model-Free RL in Non-Stationary Episodic MDPs

We consider model-free reinforcement learning (RL) in non-stationary Markov decision processes (MDPs). Both the reward functions and the state transition distributions are allowed to vary over time, either gradually or abruptly, as long as their cumulative variation magnitude does not exceed certain budgets. We propose an algorithm, named Restarted Q-Learning with Upper Confidence Bounds (RestartQ-UCB), for this setting, which adopts a simple restarting strategy and an extra optimism term. Our algorithm outperforms the state-of-the-art (model-based) solution in terms of dynamic regret. Specifically, RestartQ-UCB with Freedman-type bonus terms achieves a dynamic regret of $\widetilde{O}(S^{\frac{1}{3}} A^{\frac{1}{3}} \Delta^{\frac{1}{3}} H T^{\frac{2}{3}})$, where $S$ and $A$ are the numbers of states and actions, respectively, $\Delta>0$ is the variation budget, $H$ is the number of steps per episode, and $T$ is the total number of steps. We further show that our algorithm is near-optimal by establishing an information-theoretical lower bound of $\Omega(S^{\frac{1}{3}} A^{\frac{1}{3}} \Delta^{\frac{1}{3}} H^{\frac{2}{3}} T^{\frac{2}{3}})$, which to the best of our knowledge is the first impossibility result in non-stationary RL in general.

Reinforcement Learning for Non-Stationary Markov Decision Processes: The Blessing of (More) Optimism

We consider un-discounted reinforcement learning (RL) in Markov decision processes (MDPs) under drifting non-stationarity, i.e., both the reward and state transition distributions are allowed to evolve over time, as long as their respective total variations, quantified by suitable metrics, do not exceed certain variation budgets. We first develop the Sliding Window Upper-Confidence bound for Reinforcement Learning with Confidence Widening (SWUCRL2-CW) algorithm, and establish its dynamic regret bound when the variation budgets are known. In addition, we propose the Bandit-over-Reinforcement Learning (BORL) algorithm to adaptively tune the SWUCRL2-CW algorithm to achieve the same dynamic regret bound, but in a parameter-free manner, i.e., without knowing the variation budgets. Notably, learning non-stationary MDPs via the conventional optimistic exploration technique presents a unique challenge absent in existing (non-stationary) bandit learning settings. We overcome the challenge by a novel confidence widening technique that incorporates additional optimism.